Precalculus Index Cards
One of the most common student questions is:
‘What do I need to know?’
Answer: the ‘Index Card Method’
When I teach, every concept becomes an index card (4" x 6", blank both sides—it's easier to write math without lines). The cards guide class discussions.
Students hand-copy the cards (adding additional information, as needed). By the end of the course, they have a stack that embodies every key idea. Cards can be mixed up so learning isn't order-dependent; ones that are well understood are taken out to focus on those that remain.
Students hold the whole course in the palm of their hand.
I used this method for decades of teaching. Early on, the classroom blackboard became ‘one side of a card’: as I lectured, the card contents emerged on the board, and students took notes. Later on, students got photo-copies of cards, or they were posted on the web. Many-a-student has told me (years later) that they still have their stack of cards!
These are not typical ‘flash cards’, which might have (say) a theorem name on one side and statement on the other. Instead, they have enough meat to form the basis for a complete precalculus course—just not much fat or gravy! They've been fine-tuned: with only 4" x 6" of space, what is the essential content to include, and what's the best way to say it?
GET THE INDEX CARDS
To get the set of (digital) index cards, click the ‘Download’ button:
You'll get all $\,107\,$ cards (jpg files): cards $1$–$100$, plus RVW, 4cd, 4ef, 8.5ab, 12.5, 17cd, and 17ef.
Below are snapshots of the index cards. (Yep, that's my handwriting!) Click on any card to see a bigger image.
You can see the cards used in the context of a year-long high school course here. It's an old web page, and has a very different style!
Students: These cards are a great resource, even if your teacher isn't using the ‘index card method’. Just be sure you write them up yourself. Even though you could certainly print them out (or even cut-and-tape them onto actual index cards), you won't get the full benefit unless you create them yourself.
Beneath each index card are links to the corresponding lessons in my online Precalculus course.
To clarify handwriting and abbreviations, there's a ‘transcript’ button above each image.
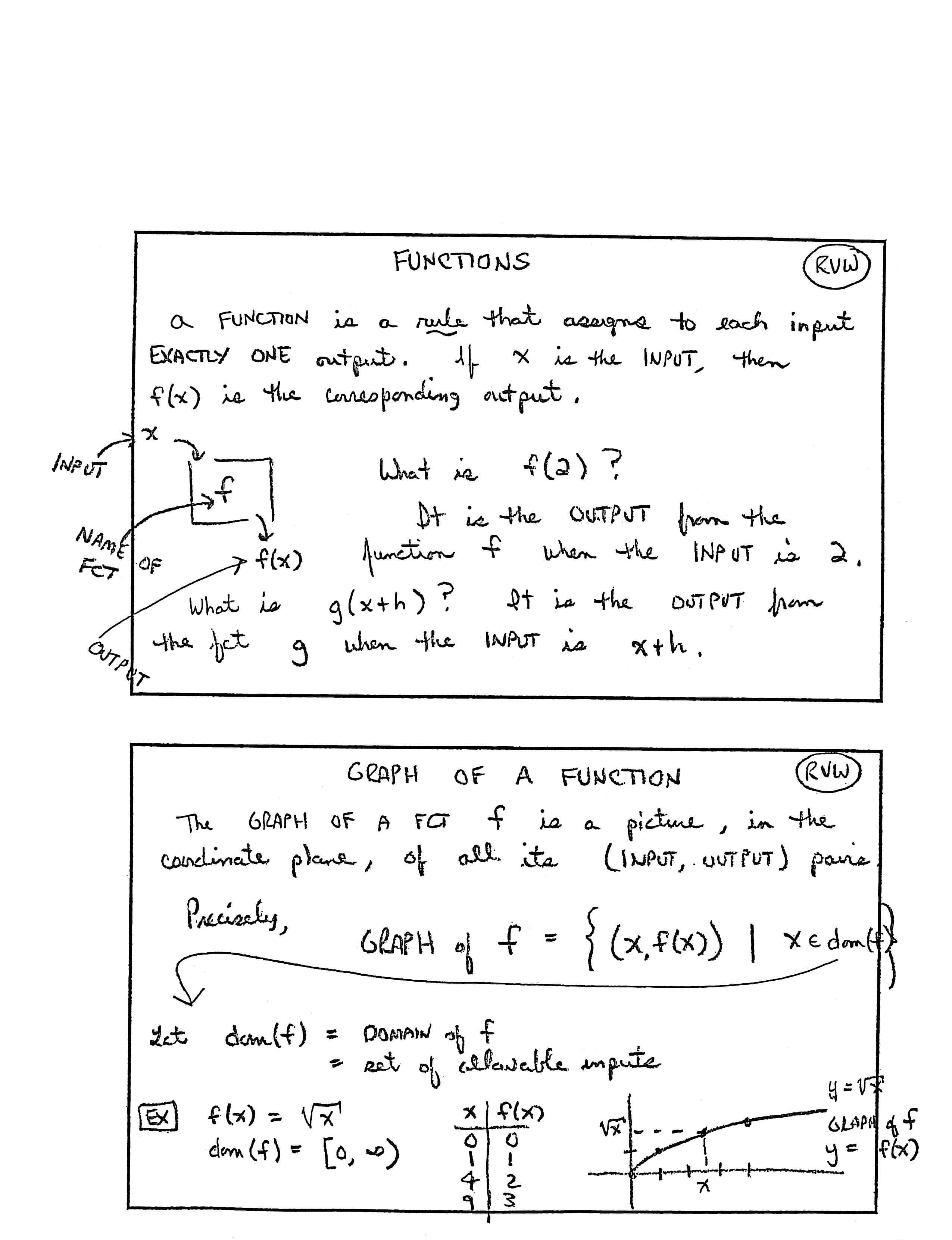
FUNCTIONS
A FUNCTION is a rule that assigns to each input EXACTLY ONE output. If $\,x\,$ is the INPUT, then $\,f(x)\,$ is the corresponding output.
[labels on graphic] INPUT $\,x\,,$ NAME OF FCT $\,f\,,$ OUTPUT $\,f(x)$
What is $\,f(2)\,$? It is the OUTPUT from the function $\,f\,$ when the INPUT is $\,2\,.$
What is $\,g(x+h)\,$? It is the OUTPUT from the fct $\,g\,$ when the INPUT is $\,x+h\,.$
GRAPH OF A FUNCTION
The GRAPH OF A FCT $\,f\,$ is a picture, in the coordinate plane, of all its (INPUT,OUTPUT) pairs.
Precisely,
$$ \text{GRAPH OF $\,f$} = \{(x,f(x))\ |\ x\in\text{dom}(f)\} $$Let
$$ \begin{align} \text{dom}(f) &= \text{DOMAIN OF $\,f$}\cr &= \text{set of allowable inputs} \end{align} $$
EX:
$\,f(x) = \sqrt{x}$
$\text{dom}(f) = [0,\infty]$
| $x$ | $f(x)$ |
| $0$ | $0$ |
| $1$ | $1$ |
| $4$ | $2$ |
| $9$ | $3$ |
[labels on graph] point $\,(x,\sqrt x)\,,$ $\,y = \sqrt x\,,$ GRAPH OF $\,f\,,$ $\,y = f(x)$
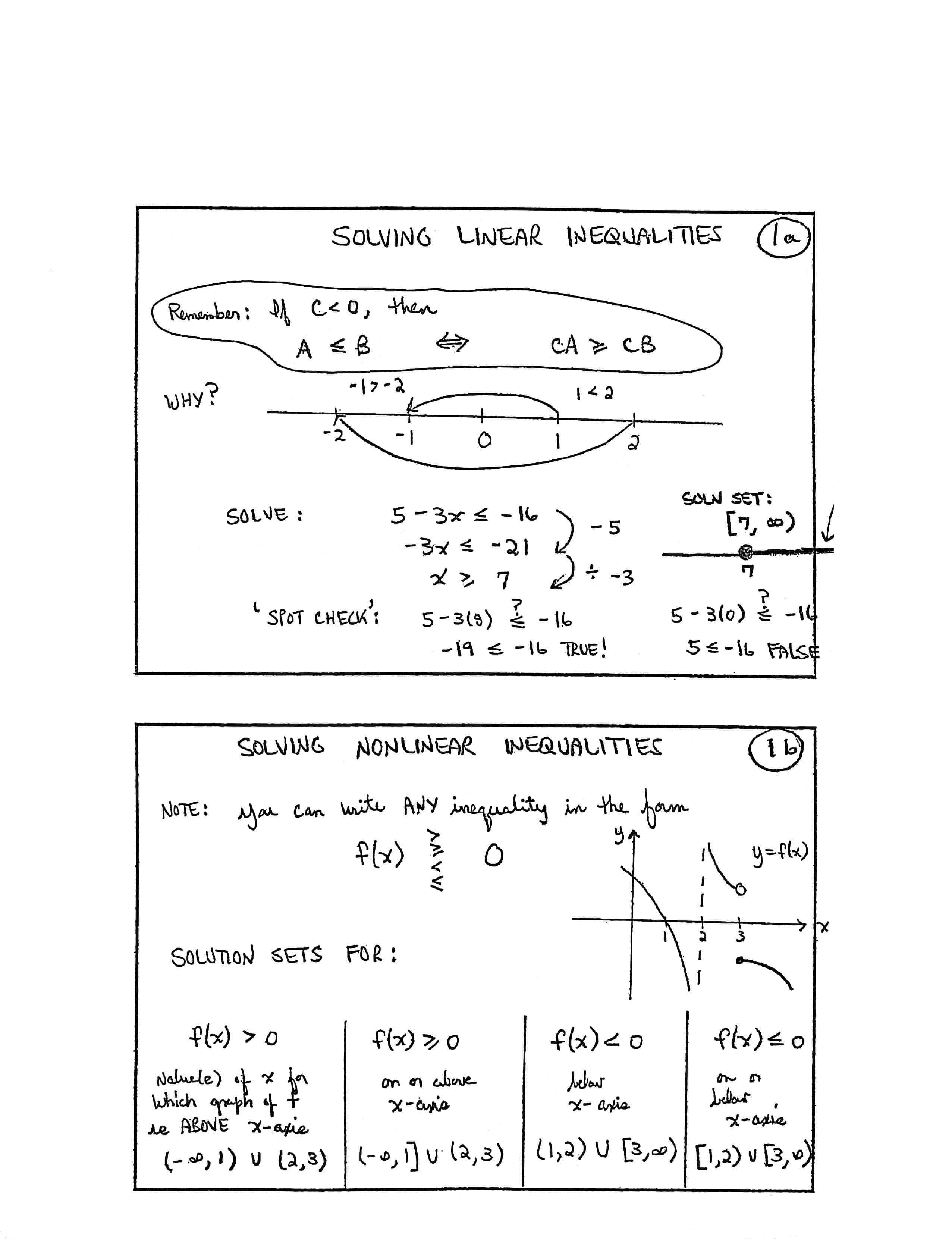
Solving Nonlinear Inequalities in One Variable (Introduction)
SOLVING LINEAR INEQUALITIES
Remember: If $\,C\lt 0\,,$ then
$$A\le B\ \ \iff\ \ CA\ge CB$$[labels on image] Why? $\,-1\ge -2\,,$ $\,1\lt 2\,,$ tick marks $\,-2\,,$ $\,-1\,,$ $\,0\,,$ $\,1\,,$ $\,2$
SOLVE:
$$ \begin{gather} 5-3x\le -16\cr \text{(subtract $5$)}\cr\cr -3x\le -21\cr \text{(divide by $-3$)}\cr\cr x\ge 7 \end{gather} $$SOLN SET: $\,[7,\infty)$
‘SPOT CHECK’:
$$ \begin{gather} 5 - 3(8) \overset{?}{\le} -16\cr -19 \le -16\ \ \text{TRUE!}\cr\cr 5 - 3(0) \overset{?}{\le} -16\cr 5 \le -16\ \ \text{FALSE} \end{gather} $$SOLVING NONLINEAR INEQUALITIES
Note: You can write ANY inequality in the form
$$ f(x)\ \substack{ \gt\strut \\ \ge\strut \\ \lt\strut \\ \le\strut }\ 0 $$[label on graph] $\,y = f(x)$
SOLUTION SETS FOR:
$f(x) \gt 0$
value(s) of $\,x\,$ for which graph of $\,f\,$ is ABOVE
$x$-axis
$(-\infty,1) \cup (2,3)$
$f(x) \ge 0$
on or above
$x$-axis
$(-\infty,1] \cup (2,3)$
$f(x) \lt 0$
below
$x$-axis
$(1,2) \cup [3,\infty)$
$f(x) \le 0$
on or below
$x$-axis
$[1,2) \cup [3,\infty)$

KEY IDEA for solving NONLINEAR INEQUALITIES
There are only $\,2\,$ TYPES OF PLACES where the graph of a function $\,f\,$ can go from above to below the $x$-axis (or vice versa):
- where $\,f(x) = 0$
- where there's a BREAK in the graph of $\,f$
the TEST POINT METHOD for solving NONLINEAR INEQUALITIES
- Get $\,0\,$ on one side; identify $\,f(x)\,.$
- Where is $\,f(x) = 0\,$? Break(s) in graph? Mark these on a # line: $\,B\,,z$
- TEST resulting subintervals. (MAY USE a graphing calculator—SHOW GRAPH!)
- REPORT SOLUTION SET
- ‘SPOT-CHECK’ in ORIGINAL SENTENCE

EXAMPLE: Using the TP METHOD
Solve: $\,x^2 + 5x \gt -6\,$ (ORIGINAL SENTENCE)
(1) $\,\underbrace{x^2 + 5x + 6}_{f(x)} \gt 0$
(2)
$\,x^2 + 5x + 6 = 0$
$(x+2)(x+3) = 0$
(3) (test subintervals)
[labels on number line]
$T = -4\ \ (-)(-)$
$T = -2.5\ (-)(+)$
$T = 0\ \ (+)(+)$
zeros at $\,-3\,$ and $\,-2$
(4) SOLN SET to $\,f(x) \gt 0\,$: $(-\infty,-3) \cup (-2,\infty)$
(5) $$ \begin{gather} (-4)^2 + 5(-4) \overset{?}{\gt} -6\cr 16 - 20 \overset{?}{\gt} -6\cr -4 \gt -6\ \ \text{True!}\cr\cr (-2.5)^2 + 5(-2.5) \overset{?}{\gt} -6\cr -6.25 \gt -6\ \ \text{False!} \end{gather} $$
EXAMPLE: Using the TP METHOD
Solve: $\,x\le \frac{2}{x-1}\,$ (ORIGINAL SENTENCE)
(1) $$ \begin{gather} x - \frac 2{x-1}\le 0\cr\cr \frac{x(x-1)-2}{x-1}\le 0\cr\cr \frac{x^2 - x - 2}{x-1}\le 0\cr\cr \underbrace{\frac{(x-2)(x+1)}{x-1}}_{f(x)}\le 0 \end{gather} $$
(2) and (3)
[labels on number line]
zero at $\,-1\,,$ break at $\,1\,,$
zero at $\,2$
(4) Soln set to $\,f(x) \le 0\,$: $(-\infty,-1] \cup (1,2]$
(5) $$ \begin{gather} 0 \overset{?}{\le} \frac 2{0-1}\cr\cr 0 \le -2\cr\ \text{False!}\cr\cr -2 \overset{?}{\le} \frac{2}{-2-1}\cr\cr -2 \overset{?}{\le} \frac{-2}3\cr \text{True!} \end{gather} $$
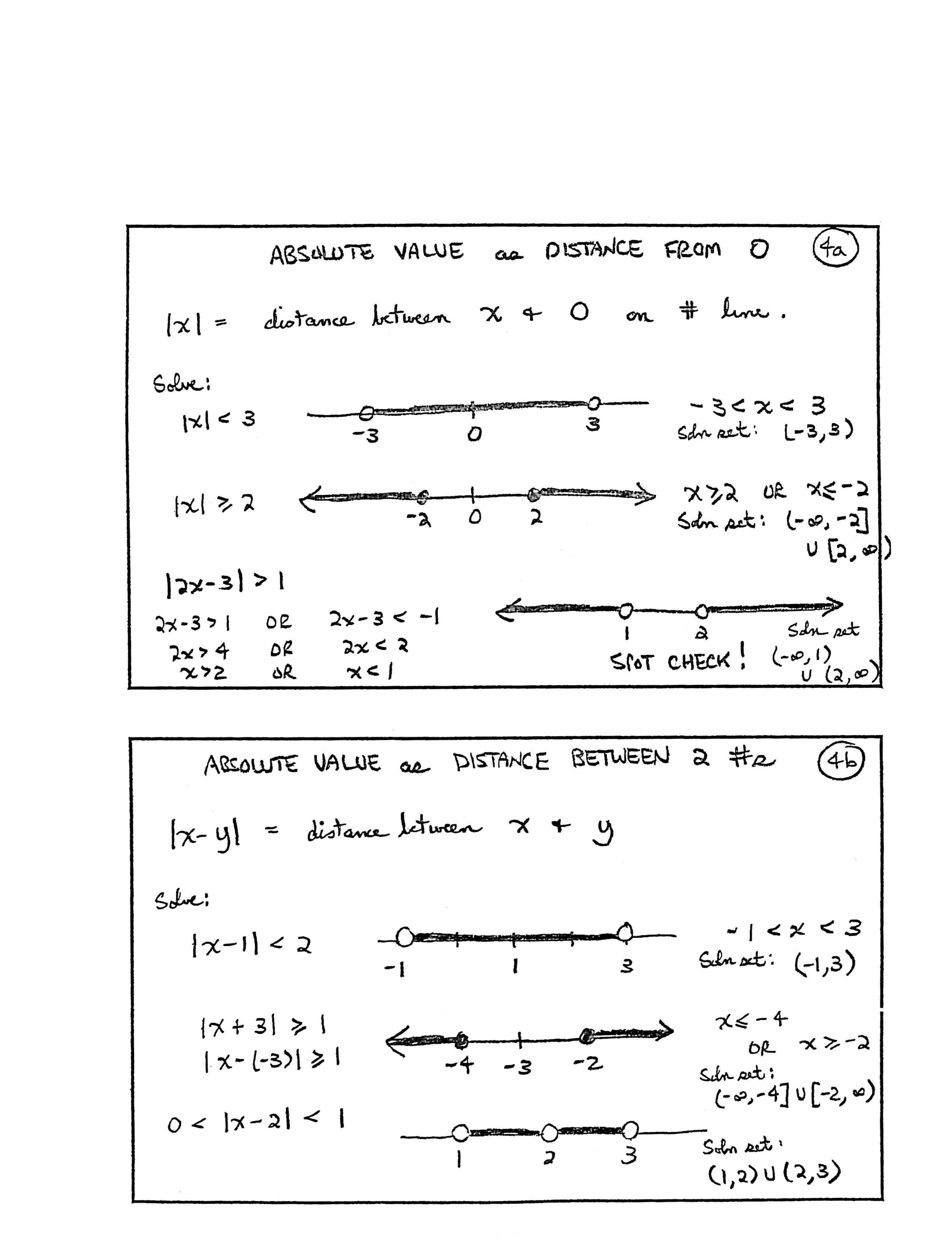
ABSOLUTE VALUE as DISTANCE FROM $\,0$
$|x| = \,$ distance between $\,x\,$ and $\,0\,$ on # line.
Solve:
$|x|\lt 3\,,$ $\,-3 \lt x \lt 3\,,$ Soln set: $\,(-3,3)$
Solve:
$|x|\ge 2\,,$ $\,x\ge 2\ \ \text{or}\ \ x\le -2\,,$ Soln set: $\,(-\infty,-2] \cup (2,\infty)$
SPOT CHECK!
Soln set $\,(-\infty,1)\cup (2,\infty)$
ABSOLUTE VALUE as DISTANCE BETWEEN $\,2\,$ NUMBERS
$|x-y| = \,$ distance between $\,x\,$ and $\,y$
Solve:
$|x-1| \lt 2\,,$ $\,-1 \lt x \lt 3\,,$ Soln set: $\,(-1,3)$
$x\le -4\ \ \text{or}\ \ x\ge -2\,,$ Soln set: $\,(-\infty,-4] \cup [-2,\infty)$
$0 \lt |x-2| \lt 1\,,$ Soln set: $\,(1,2)\cup (2,3)$

CIRCLES
Let $\,(x,y)\,$ be ANY point on the circle with center $\,(h,k)\,$ and radius $\,r\,.$ Then,
$$ \begin{align} &\text{distance from $\,(h,k)\,$ to $\,(x,y)\,$}\cr &\quad = \sqrt{(x-h)^2 + (y-k)^2}\cr &\quad = r \end{align} $$
EQUATION OF CIRCLE with CENTER $\,(h,k)\,$ and RADIUS $\,r$
$(x-h)^2 + (y-k)^2 = r^2$
If you multiply out:
- COEFFICIENTS of $\,x^2\,$ and $\,y^2\,$ are the SAME
- NO $\,xy\,$ TERM
- MAY HAVE $\,x\,,$ $\,y\,,$ CONSTANT TERMS
COMPLETING THE SQUARE TECHNIQUE
EXAMPLE:
GRAPH: $\,4x^2 + 4y^2 - 8x + 16y = -19$
Circle with CENTER $\,(1,-2)\,,$ RADIUS $\,\frac 12$
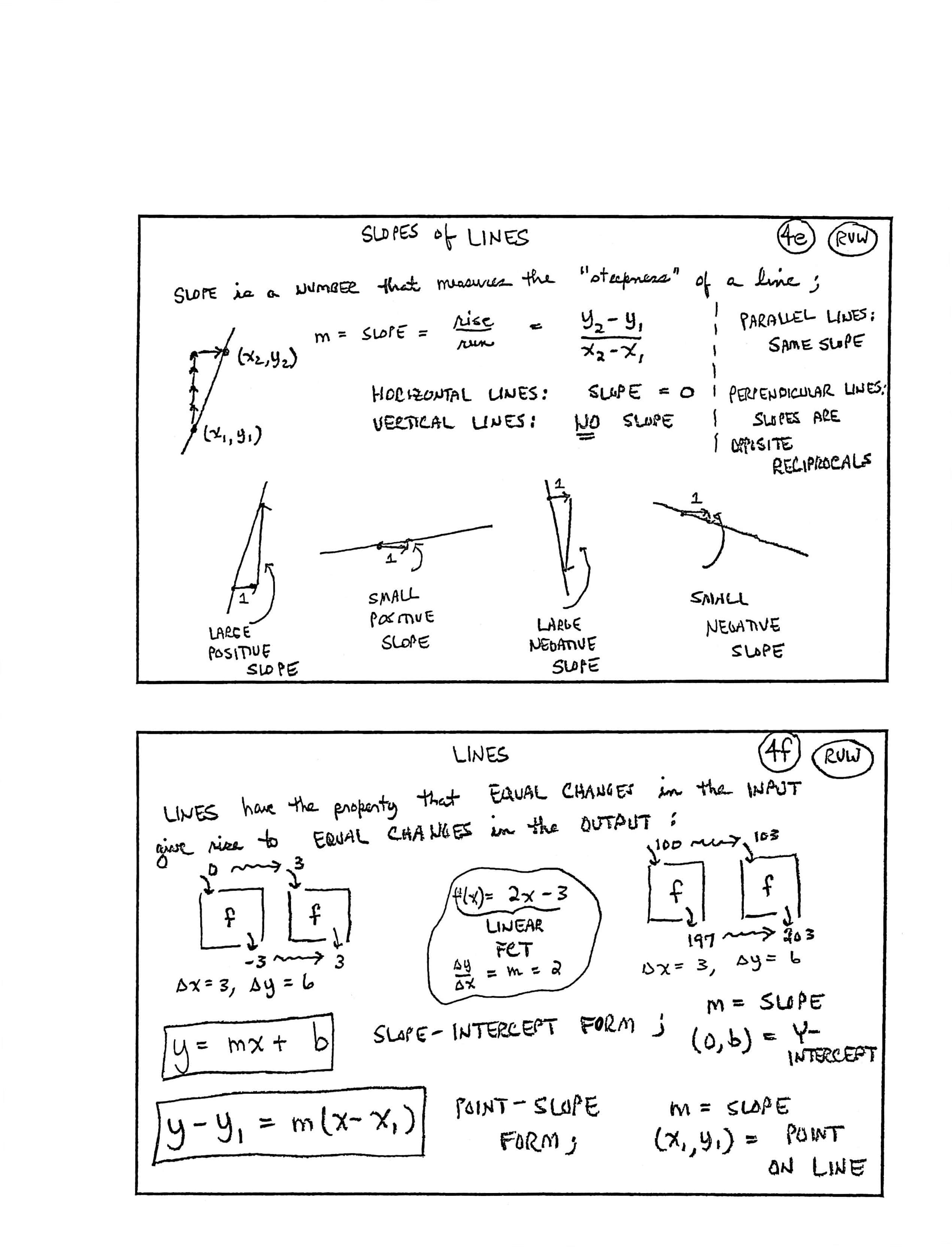
SLOPES of LINES
SLOPE is a NUMBER that measures the “steepness” of a line;
$$ m = \text{SLOPE} = \frac{\text{rise}}{\text{run}} = \frac{y_2-y_1}{x_2-x_1} $$
HORIZONTAL LINES: SLOPE $= 0$
VERTICAL LINES: NO SLOPE
PARALLEL LINES: SAME SLOPE
PERPENDICULAR LINES: SLOPES ARE OPPOSITE RECIPROCALS
LARGE POSITIVE SLOPE; SMALL POSITIVE SLOPE; LARGE NEGATIVE SLOPE; SMALL NEGATIVE SLOPE
LINES
LINES have the property that EQUAL CHANGES in the INPUT give rise to EQUAL CHANGES in the OUTPUT:
$$ \begin{gather} \underbrace{f(x) = 2x - 3}_{\text{LINEAR FCT}}\cr\cr \frac{\Delta y}{\Delta x} = m = 2 \end{gather} $$
$0$ into $\,f\,$ box, $-3\,$ comes out
$3$ into $\,f\,$ box, $3\,$ comes out
$\Delta x = 3\,,$ $\,\Delta y = 6$
$100$ into $\,f\,$ box, $197\,$ comes out
$103$ into $\,f\,$ box, $203\,$ comes out
$\Delta x = 3\,,$ $\,\Delta y = 6$
$y = mx+b$
SLOPE-INTERCEPT FORM;
$m = $ SLOPE
$(0,b) = $ $y$-INTERCEPT
$y - y_1 = m(x - x_1)$
POINT-SLOPE FORM;
$m = $ SLOPE
$(x_1,y_1) = \text{POINT ON LINE}$
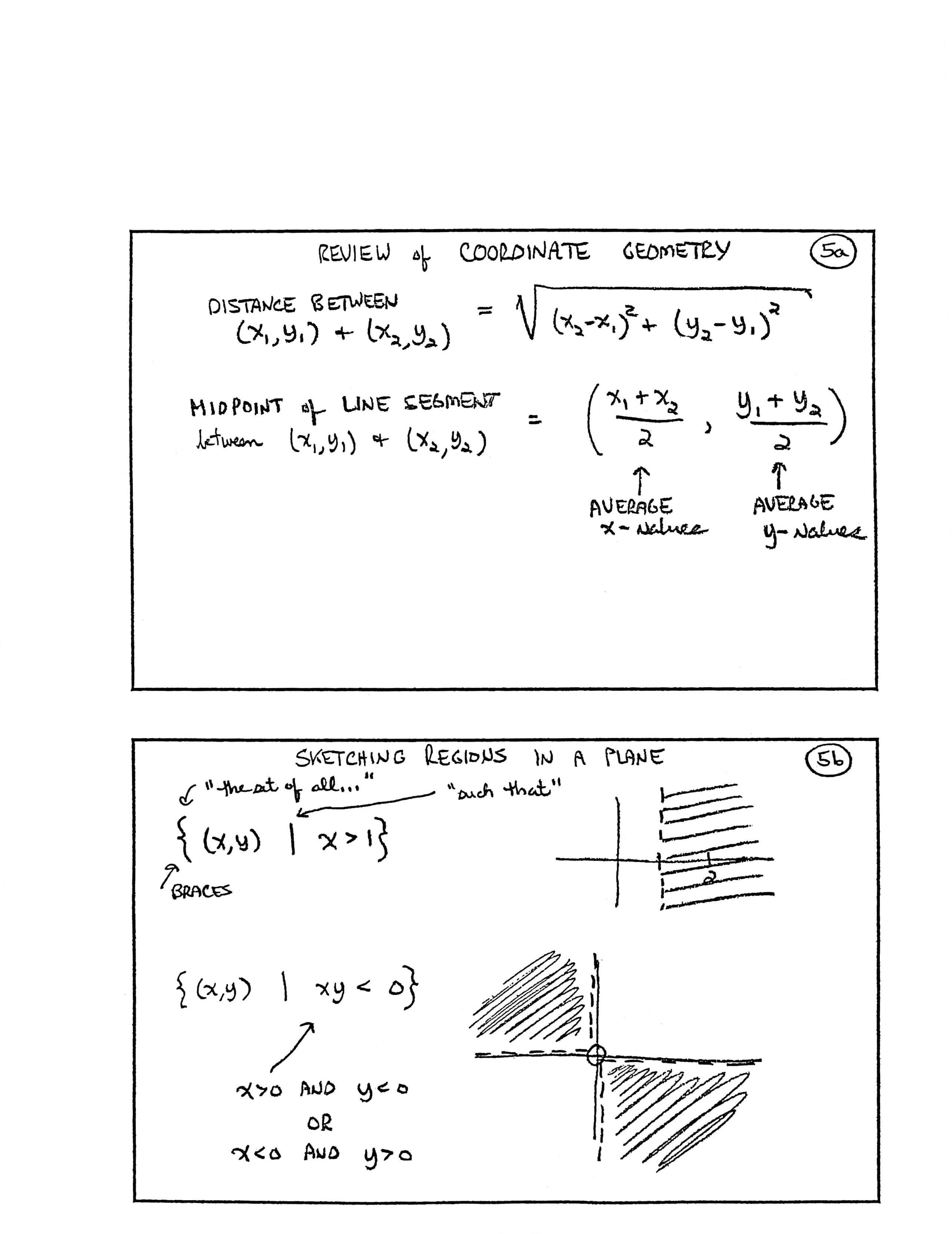
REVIEW of COORDINATE GEOMETRY
$$ \begin{gather} \text{DISTANCE BETWEEN}\ (x_1,y_1)\ \text{and}\ (x_2,y_2)\cr = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2} \end{gather} $$$$ \begin{gather} \text{MIDPOINT of LINE SEGMENT}\cr \text{between} \ (x_1,y_1)\ \text{and}\ (x_2,y_2)\cr = \biggl( \underset{\substack{\uparrow \\ \text{AVERAGE}\\ x-\text{values}}}{\frac{x_1 + x_2}2} \ ,\ \underset{\substack{\uparrow \\ \text{AVERAGE}\\ y-\text{values}}}{\frac{y_1+y_2}2} \biggr) \end{gather} $$
SKETCHING REGIONS IN A PLANE
$$ \overset{\substack{\text{the set of all ...}}\\ \qquad \downarrow}{\bigl\{ } (x,y)\ \overset{\substack{\text{such that}\\ \downarrow}}{\ |}\ x\gt 1 \overset{\substack{\text{BRACES}\\ \downarrow}}{\ \bigr\} } $$$$ \bigl\{ (x,y)\ |\ \underset{\substack{\uparrow\\ x\gt 0\text{ and } y\lt 0\\ \text{OR}\\ x\lt 0\text{ and } y\gt 0}}{xy \lt 0} \bigr\} $$
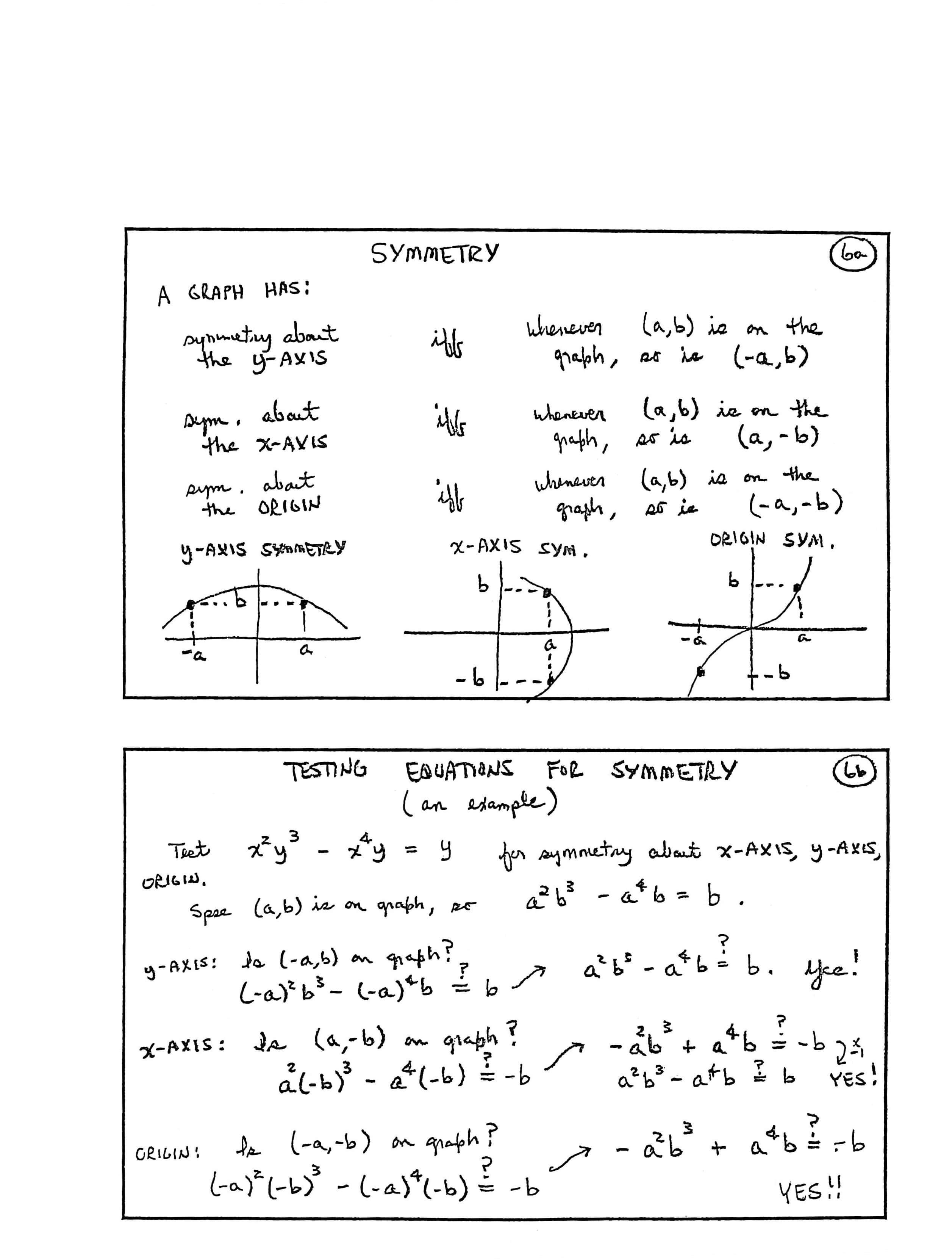
SYMMETRY
A GRAPH HAS:
| symmetry about the $y$-AXIS | iff [if and only if] |
whenever $\,(a,b)\,$ is on the graph, so is $\,(-a,b)$ |
| symmetry about the $x$-AXIS | iff | whenever $\,(a,b)\,$ is on the graph, so is $\,(a,-b)$ |
| symmetry about the ORIGIN | iff | whenever $\,(a,b)\,$ is on the graph, so is $\,(-a,-b)$ |
$y$-AXIS SYMMETRY, $x$-AXIS SYMMETRY, ORIGIN SYMMETRY
TESTING EQUATIONS FOR SYMMETRY (an example)
Test $\,x^2y^3 - x^4y = y\,$ for symmetry about $x$-AXIS, $y$-AXIS, ORIGIN.
Spse [suppose] $\,(a,b)\,$ is on graph, so $\,a^2b^3 - a^4b = b\,.$
| $y$-axis: |
Is $\,(-a,b)\,$ on graph? $(-a)^2b^3 - (-a)^4b \overset{?}{=} b$ $a^2b^3 - a^4b \overset{?}{=} b$ |
Yes! |
| $x$-axis: |
Is $\,(a,-b)\,$ on graph? $a^2(-b)^3 - a^4(-b) \overset{?}{=} b$ $-a^2b^3 + a^4b \overset{?}{=} -b$ ($\times -1$) $a^2b^3 - a^4b \overset{?}{=} b$ |
Yes! |
| ORIGIN: |
Is $\,(-a,-b)\,$ on graph? $(-a)^2(-b)^3 - (-a)^4(-b) \overset{?}{=} -b$ $-a^2b^3 + a^4b \overset{?}{=} -b$ |
Yes! |
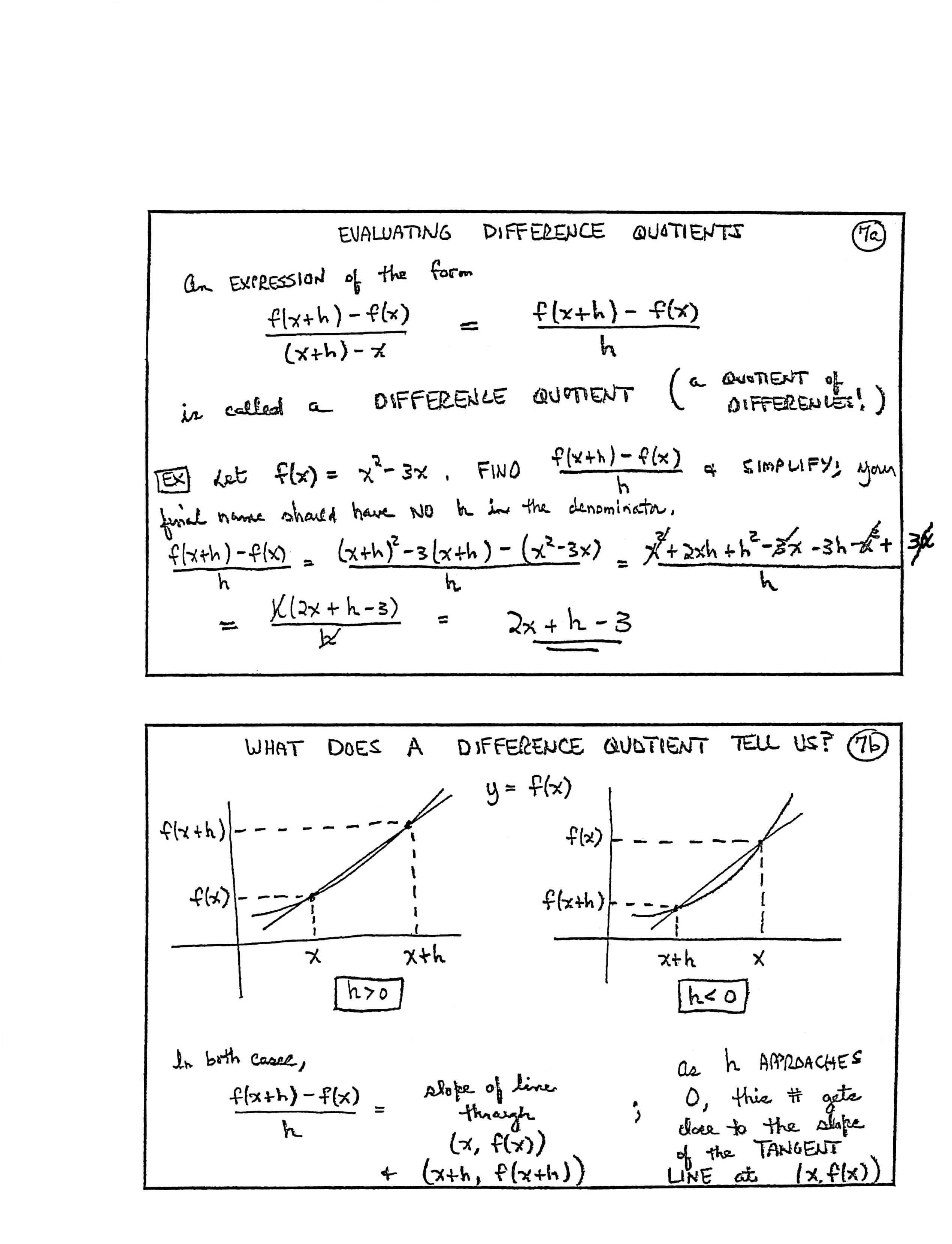
EVALUATING DIFFERENCE QUOTIENTS
An EXPRESSION of the form
$$ \frac{f(x+h)-f(x)}{(x+h)-x} = \frac{f(x+h)-f(x)}h $$is called a DIFFERENCE QUOTIENT (a QUOTIENT of DIFFERENCES!)
Example: Let $\,f(x) = x^2 - 3x\,.$ FIND $\frac{f(x+h)-f(x)}h\,$ and SIMPLIFY; your final name should have NO $\,h\,$ in the denominator.
$$ \begin{align} &\frac{f(x+h) - f(x)}h\cr\cr &\quad = \frac{(x+h)^2 - 3(x+h) - (x^2-3x)}{h}\cr\cr &\quad = \frac{\cancel{x^2} + 2xh + h^2 - \cancel{3x} - 3h - \cancel{x^2} + \cancel{3x}}h\cr\cr &\quad = \frac{\cancel{h}(2x +h-3)}{\cancel{h}}\cr\cr &\quad = 2x + h - 3 \end{align} $$WHAT DOES A DIFFERENCE QUOTIENT TELL US?
[labels on graphs] $\,y = f(x)\,,$ points $\,\bigl(x,f(x)\bigr)\,$ and $\,\bigl(x+h,f(x+h)\bigr)\,,$ $\,h\gt 0\,,$ $\,h\lt 0$
In both cases,
$$ \begin{align} &\frac{f(x+h)-f(x)}h\cr &\quad = \text{slope of line through}\cr &\qquad \bigl(x,f(x)\bigr) \ \text{and}\ \bigl(x+h,f(x+h)\bigr)\ ; \end{align} $$as $\,h\,$ APPROACHES $\,0\,,$ this number gets close to the slope of the TANGENT LINE at $\,\bigl(x,f(x)\bigr)\,$
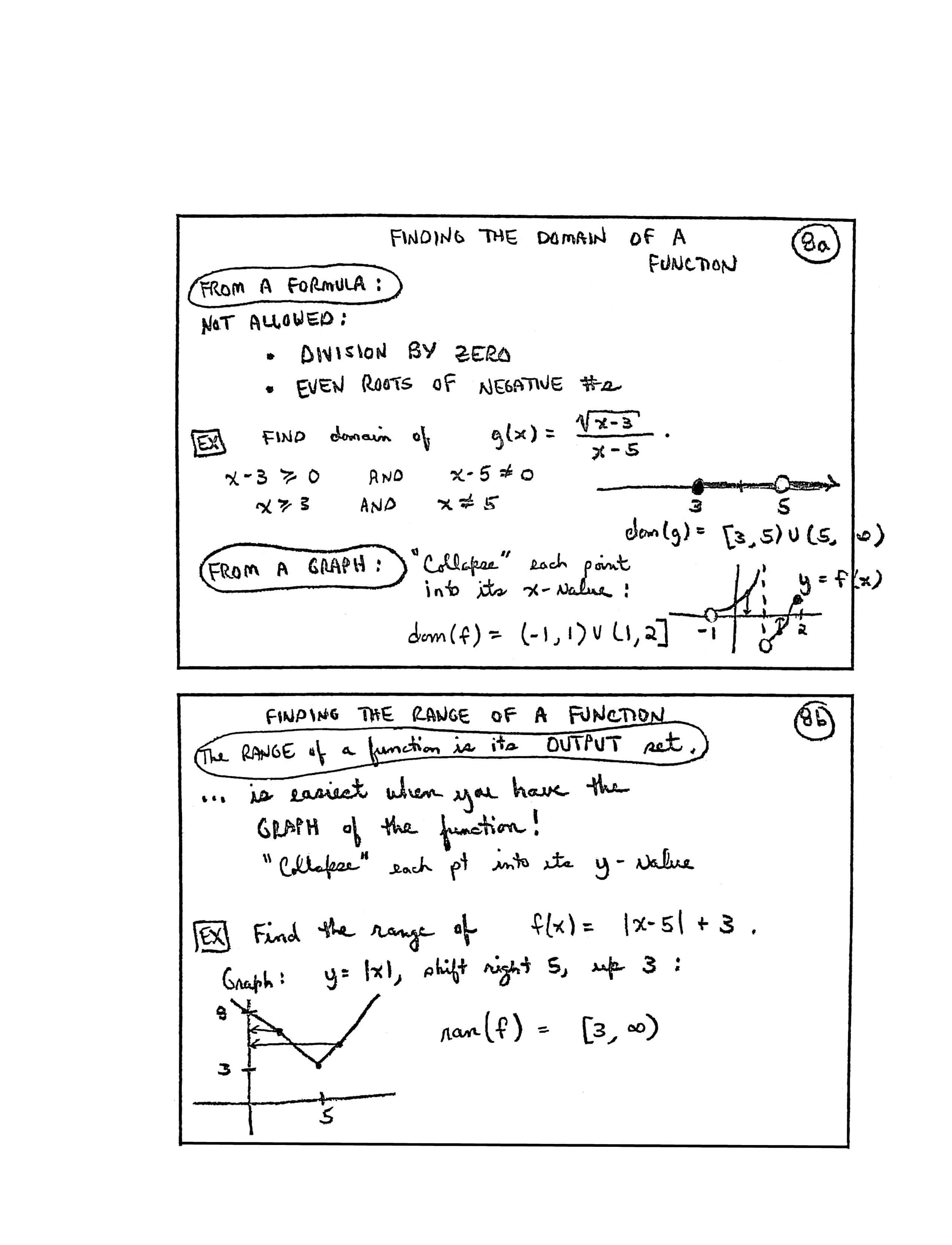
FINDING THE DOMAIN OF A FUNCTION
FROM A FORMULA:
NOT ALLOWED:
- DIVISION BY ZERO
- EVEN ROOTS OF NEGATIVE NUMBERS
Example: FIND domain of $\,g(x) = \frac{\sqrt{x-3}}{x-5}\,.$
$$ \begin{gather} x-3\ge 0\ \ \text{AND}\ \ x-5\ne 0\cr\cr x\ge 3\ \ \text{AND}\ \ x\ne 5\cr\cr \text{dom}(g) = [3,5)\cup (5,\infty) \end{gather} $$FROM A GRAPH:
“Collapse” each point into its $x$-value:
$$ \text{dom}(f) = (-1,1)\cup (1,2] $$[label on graph] $y = f(x)$
FINDING THE RANGE OF A FUNCTION
The RANGE of a function is its OUTPUT set.
... is easiest when you have the GRAPH of the function!
“Collapse’ each pt [point] into its $y$-value.
Example: Find the range of $\,f(x) = |x-5| + 3\,.$
Graph: $\,y = |x|\,,$ shift right $\,5\,,$ up $\,3\,$:
$$ \text{ran}(f) = [3,\infty) $$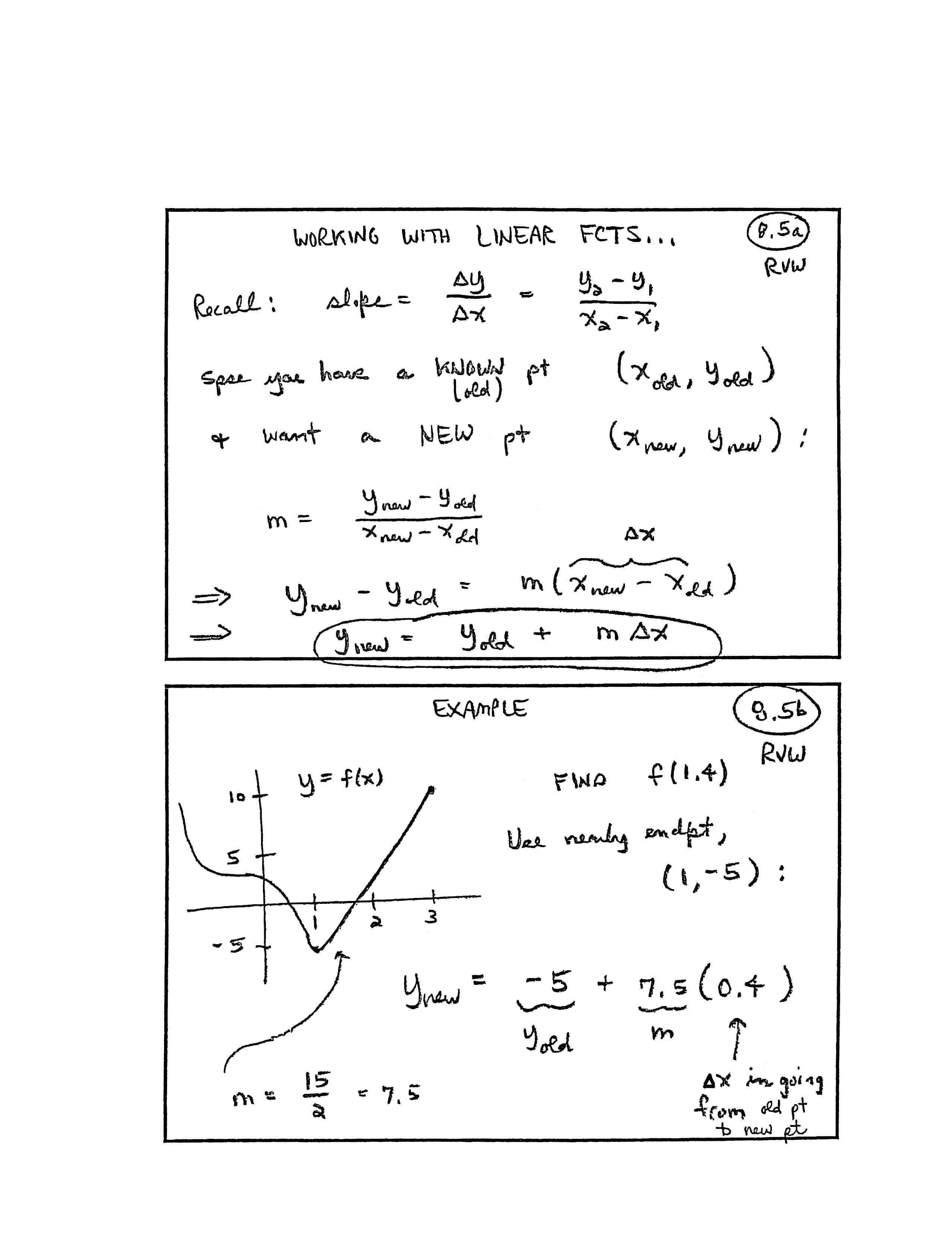
WORKING WITH LINEAR FCTS [functions]...
Recall: $\,\text{slope} = \frac{\Delta y}{\Delta x} = \frac{y_2-y_1}{x_2-x_1}$
Spse [suppose] you have a KNOWN (old) pt [point] $\,(x_{\text{old}},y_{\text{old}})\,$ and want a NEW pt $\,(x_{\text{new}},y_{\text{new}})\,$:
$$ \begin{align} &m = \frac{y_{\text{new}} - y_{\text{old}}}{x_{\text{new}} - x_{\text{old}}}\cr &\quad\implies y_{\text{new}} - y_{\text{old}} = m(\overbrace{x_{\text{new}} - x_{\text{old}}}^{\Delta x})\cr\cr &\quad\implies y_{\text{new}} = y_{\text{old}} + m\Delta x \end{align} $$EXAMPLE
Find $\,f(1.4)\,.$ Use nearby endpt [endpoint] $\,(1,-5)\,$:
[labels on graph] points $\,(1,-5)\,$ and $\,(3,10)\,,$ $\,y = f(x)\,,$ $\,m = \frac{15}2 = 7.5$
$$ y_{\text{new}} = \underbrace{-5}_{y_{\text{old}}} + \underbrace{7.5}_m \underset{ \substack{\uparrow \\ \text{$\Delta x\,$ in going}\\ \text{from old pt}\\ \text{to new pt}}}{(0.4)} $$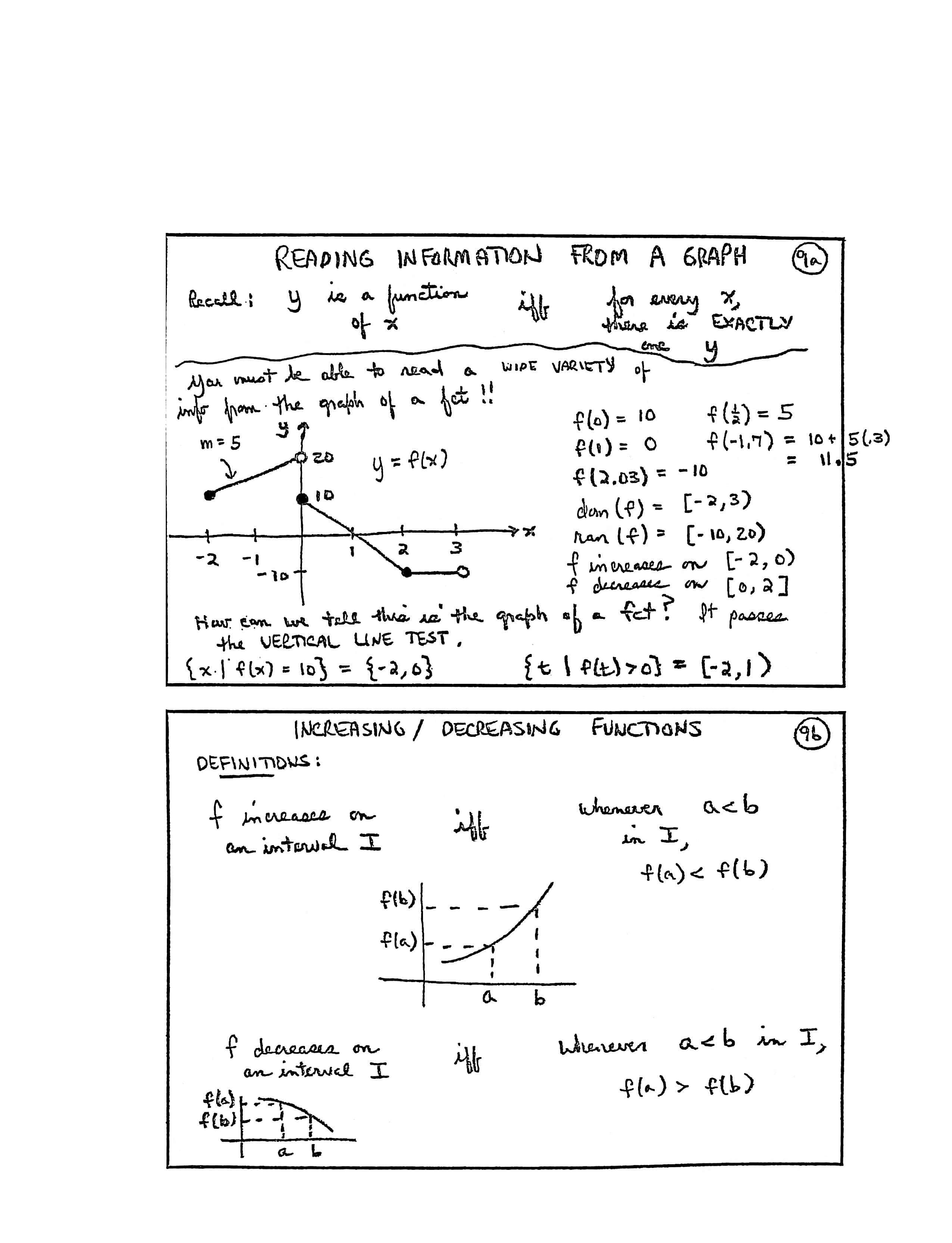
READING INFORMATION FROM A GRAPH
Recall: $\,y\,$ is a function of $\,x\,$ iff [if and only if] for every $\,x\,,$ there is EXACTLY one $\,y$
You must be able to read a WIDE VARIETY of info from the graph of a fct!!
[labels on graph] $\,m = 5\,,$ $\,y = f(x)\,,$ points $\,(-2,10)\,,\ \ (0,10)\,,\ \ (2,-10)\,$
$$ \begin{gather} f(0) = 10\cr f(\frac 12) = 5\cr f(1) = 0\cr f(-1.7) = 10 + 5(0.3) = 11.5\cr f(2.03) = -10\cr \text{dom}(f) = [-2,3)\cr \text{ran}(f) = [-10,20)\cr f \text{ increases on } [-2,0)\cr f \text{ decreases on } [0,2] \end{gather} $$How can we tell this is the graph of a fct [function]? It passes the VERTICAL LINE TEST.
$$ \begin{gather} \{x\ |\ f(x) = 10\} = \{-2,0\}\cr\cr \{t\ |\ f(t) \gt 0 \} = [-2,1) \end{gather} $$INCREASING/DECREASING FUNCTIONS
DEFINITIONS:
| $f\,$ increases on an interval $\,I$ | iff [if and only if] | whenever $\,a\lt b\,$ in $\,I\,,$ $\,f(a) \lt f(b)$ |
| $f\,$ decreases on an interval $\,I$ | iff | whenever $\,a\lt b\,$ in $\,I\,,$ $\,f(a) \gt f(b)$ |
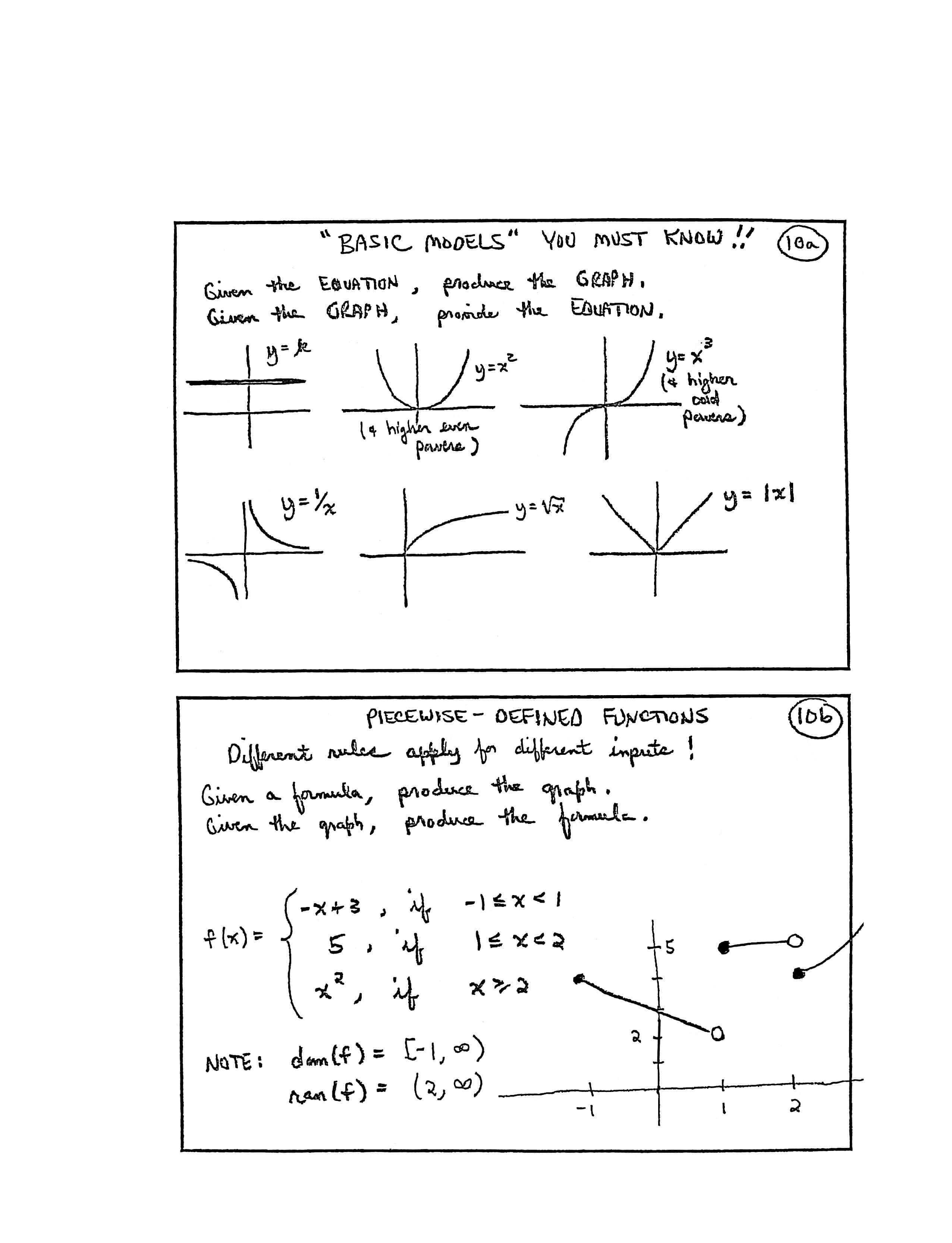
“BASIC MODELS” YOU MUST KNOW!!
Given the EQUATION, produce the GRAPH. Given the GRAPH, provide the EQUATION.
[labels on graphs] $y = k\,,$ $\,y = x^2\,$ (and higher even powers), $\,y = x^3\,$ (and higher odd powers), $\,y = \frac 1x\,,$ $\,y = \sqrt x\,,$ $\,y = |x|$
PIECEWISE-DEFINED FUNCTIONS
Different rules apply for different inputs!
Given a formula, produce the graph. Given the graph, produce the formula.
$$ f(x) = \cases{ -x+3\,, & \text{if}\ {-}1\le x\lt 1\cr 5\,, & \text{if}\ 1\le x\lt 2\cr x^2\,, & \text{if}\ x\ge 2 } $$
NOTE:
$\text{dom}(f) = [-1,\infty)$
$\text{ran}(f) = (2,\infty)$
[graph] point $\,(-1,4)\,,$ hollow dot $\,(1,2)\,,$ point $\,(1,5)\,,$ hollow dot $\,(2,5)\,,$ point $\,(2,4)$

DIRECT VARIATION
The following are EQUIVALENT (completely INTERCHANGEABLE):
- $y = kx\,,$ for $\,k\ne 0$
- $y\,$ varies directly as $\,x$
- $y\,$ is directly proportional to $\,x$
- $y\,$ is proportional to $\,x$
(The constant $\,k\,$ is called the CONSTANT OF PROPORTIONALITY.)
INVERSE VARIATION
The Following Are EQUIVALENT (TFAE):
- $y = \frac kx\,,$ for $\,k\ne 0$
- $y\,$ is inversely proportional to $\,x$
- $y\,$ varies inversely as $\,x$
TFAE:
- $z = kxy\,,$ $\,k\ne 0$
- $z\,$ varies jointly as $\,x\,$ and $\,y$
- $z\,$ is jointly proportional to $\,x\,$ and $\,y$
TFAE:
- $z = k\frac xy\,,$ $\,k\ne 0$
- $z\,$ is proportional to $\,x\,$ and inversely proportional to $\,y$

PROPORTIONALITY PROBLEMS
Write an equation for:
“$A\,$ is proportional to the square of $\,t\,$ and inversely proportional to the cube of $\,x\,.$”
$$ A = k\frac{t^2}{x^3} $$Now, if $\,A = 3\,$ when $\,t = 1\,$ and $\,x = 2\,,$ find the constant of proportionality.
$$ 3 = k\cdot \frac{1^2}{2^3}\,,\ \text{so}\ \ k = 24 $$PROPORTIONALITY PRACTICE
Write a sentence that describes the relationship:
$$y = \frac kx$$ANS [answer]: “$y\,$ varies inversely as $\,x$”
$$y = k\cdot\frac{\sqrt t}{v^2}$$ANS: “$y\,$ varies directly as the square root of $\,t\,,$ and inversely as the square of $\,v$”

What is the GRAPH of $\,y = f(x)\,$?
ANSWER: It’s the set of ALL POINTS of the form $\,\bigl(x,\underbrace{f(x)}_{y}\bigr)\,.$
Graph of $\,y = f(x+3)\,$?
Set of pts [points]:
$\,\bigl(x,f(x+3)\bigr)$
What does it mean when we say that $\,(a,b)\,$ is on the graph of $\,y = f(x)\,$?
ANS [answer]: When you substitute ‘$\,a\,$’ for ‘$\,x\,$’ and ‘$\,b\,$’ for ‘$\,y\,$’, the resulting equation is TRUE. That is, ‘$\,b = f(a)\,$’ is TRUE.
Using the “GEOMETRIC TRANSFORMATIONS” SHEET
Given ANY ENTRY in a row, be able to produce all other entries; also, UNDERSTAND why a certain change in the equation produces a certain change in the graph.
GIVEN:
GRAPH
OF $\,y = f(x)\,$;
PTS of FORM $\,\bigl(x,f(x)\bigr)$
WANTED:
GRAPH
OF $\,y = f(x) + 3\,$;
PTS of FORM $\,\bigl(x,f(x) + 3\bigr)$
[labels on graph] point $\,\bigl(x,f(x)\bigr)\,$ moves up to point $\,\bigl(x,f(x)+3\bigr)$
EACH PT [point] moves UP $\,3$
TRANSFORMATIONS INVOLVING ‘$\,y\,$’ are INTUITIVE!!

TRANSFORMATIONS INVOLVING ‘$\,x\,$’ are COUNTER-INTUITIVE ... WHY?
GIVEN: GRAPH OF
$\,y = f(x)\,$;
PTS OF FORM $\,\bigl(x,f(x)\bigr)$
WANTED: GRAPH OF
$\,y = f(x+3)\,$;
PTS OF FORM $\,\bigl(x,f(x+3)\bigr)$
[labels on graph] points $\,\bigl(x,f(x)\bigr)\,,$ $\,\bigl(x+3,f(x+3)\bigr)\,,$ and $\,\bigl(x,f(x+3)\bigr)$
Step 1: Locate $\,x+3$
Step 2: Find $\,f(x+3)$
Step 3: Plot $\,\bigl(x,f(x+3)\bigr)$
EACH PT [point] MOVES LEFT $\,3\,$!!
TRANSFORMATIONS INVOLVING ‘$\,x\,$’ ARE COUNTER-INTUITIVE!!
A TYPICAL PROBLEM
Build up $\,y = 3|{-}x+1|-5\,$ from a basic model.
| EQUATION | ACTION | GRAPHICAL RESULT |
| $y = |x|$ | BASIC MODEL | |
| $y = 3|x|$ | multiply previous $y$-values by $\,3$ | vertical stretch, factor of $\,3$ |
| $y = 3|x|-5$ | subtract $\,5\,$ from previous $y$-values | DOWN $\,5$ |
| $y = 3|x+1|-5$ | replace every $\,x\,$ with $\,x+1$ | LEFT $\,1$ |
| $y = 3|{-}x+1|-5$ | replace every $\,x\,$ with $\,-x$ | reflect about $y$-axis |
Reflecting About Axes, and the Absolute Value Transformation
Multi-Step Practice With All the Graphical Transformations
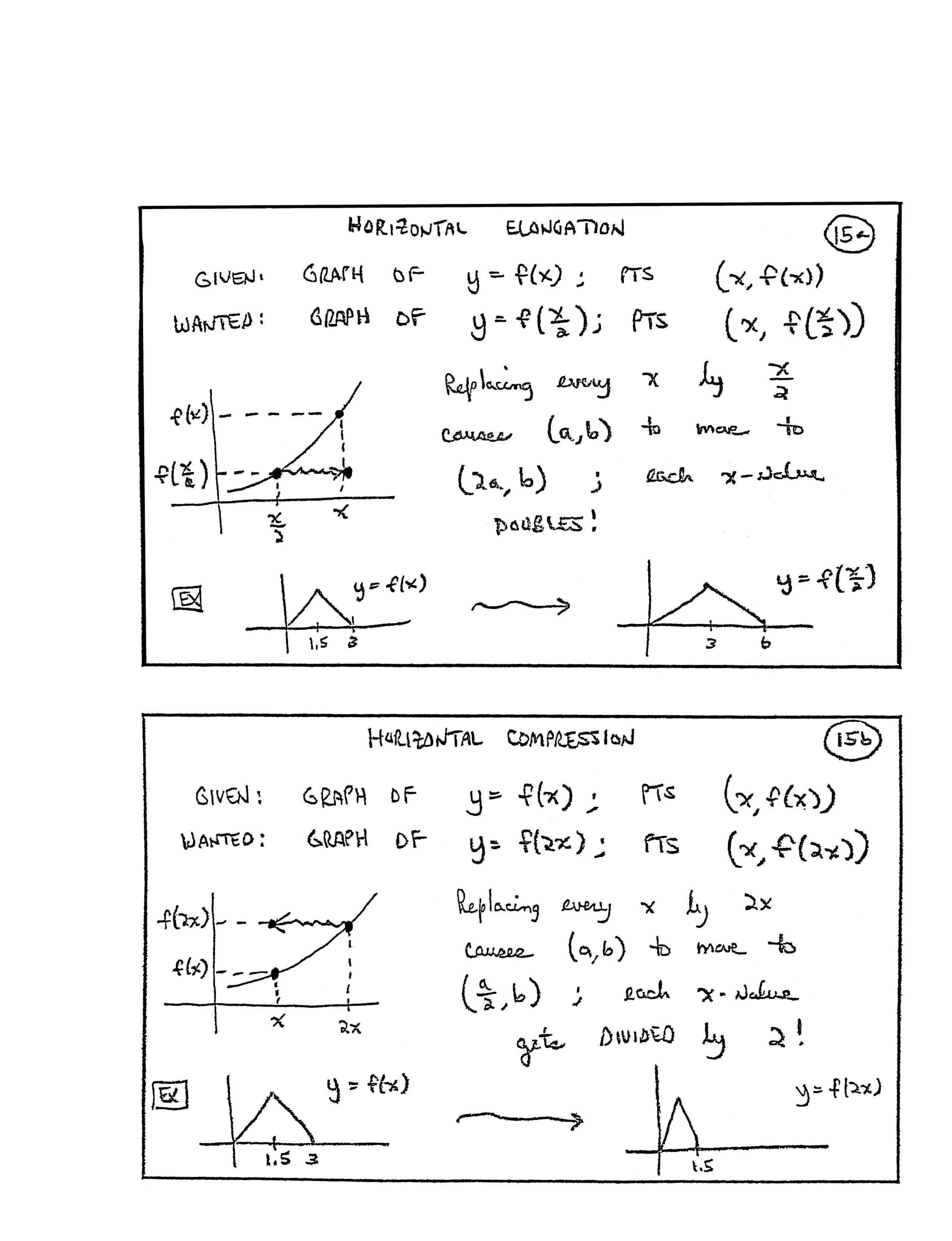
HORIZONTAL ELONGATION
GIVEN:
GRAPH OF
$\,y = f(x)\,$;
PTS [points] $\,\bigl(x,f(x)\bigr)$
WANTED:
GRAPH OF
$\,y = f(\frac x2)\,$;
PTS $\,\bigl(x,f(\frac x2)\bigr)$
[labels on graph] points $\,\bigl(\frac x2,f(\frac x2)\bigr)\,,$ $\,\bigl(x,f(\frac x2)\bigr)\,,$ $\,\bigl(x,f(x)\bigr)$
Replacing every $\,x\,$ by $\,\frac x2\,$ causes $\,(a,b)\,$ to move to $\,(2a,b)\,$; each $x$-value DOUBLES!
EX [example]
[labels on lower left graph] $\,1.5\,,$ $\,3\,,$ $\,y = f(x)$
[labels on lower right graph] $\,3\,,$ $\,6\,,$ $\,y = f(\frac x2)$
HORIZONTAL COMPRESSION
GIVEN:
GRAPH OF
$\,y = f(x)\,$;
PTS [points] $\,\bigl(x,f(x)\bigr)$
WANTED:
GRAPH OF
$\,y = f(2x)\,$;
PTS $\,\bigl(x,f(2x)\bigr)$
[labels on graph] points $\,\bigl(x,f(x)\bigr)\,,$ $\,\bigl(2x,f(2x)\bigr)\,,$ $\,\bigl(x,f(2x)\bigr)$
Replacing every $\,x\,$ by $\,2x\,$ causes $\,(a,b)\,$ to move to $\,(\frac a2,b)\,$; each $x$-value gets DIVIDED by $\,2\,$!
EX [example]
[labels on lower left graph] $\,1.5\,,$ $\,3\,,$ $\,y = f(x)$
[labels on lower right graph] $\,1.5\,,$ $\,y = f(2x)$
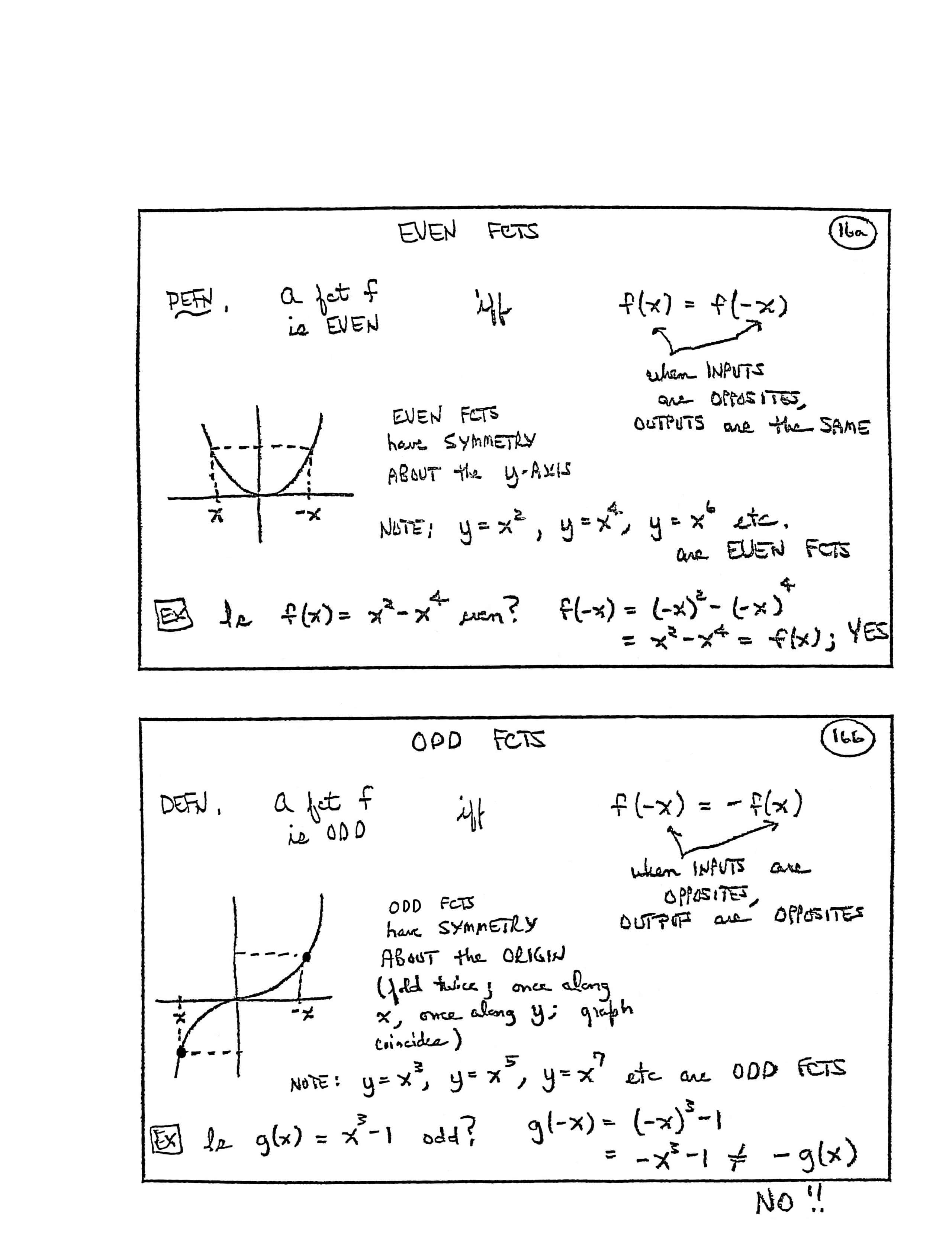
EVEN FCTS [functions]
DEFN [definition]. A fct [function] $\,f\,$ is EVEN iff [if and only if] $\,f(x) = f(-x)$
When INPUTS are OPPOSITES, OUTPUTS are the SAME.
EVEN FCTS have SYMMETRY ABOUT the $y$-AXIS.
NOTE: $\,y = x^2\,,$ $\,y = x^4\,,$ $\,y = x^6\,$ etc. are EVEN FCTS
EX [example] Is $\,f(x) = x^2 - x^4\,$ even?
$$ \begin{align} f(-x) &= (-x)^2 - (-x)^4\cr &= x^2 - x^4 = f(x)\,;\ \ \text{YES} \end{align} $$ODD FCTS
DEFN. A fct $\,f\,$ is ODD iff $\,f(-x) = -f(x)$
When INPUTS are OPPOSITES, OUTPUTS are OPPOSITES.
ODD FCTS have SYMMETRY ABOUT the ORIGIN (fold twice; once along $\,x\,,$ once along $\,y\,$; graph coincides)
NOTE: $\,y = x^3\,,$ $\,y = x^5\,,$ $\,y = x^7\,$ etc are ODD FCTS
EX [example] Is $\,g(x) = x^3 - 1\,$ odd?
$$ \begin{align} g(-x) &= (-x)^3 - 1\cr &= -x^3 - 1\ne -g(x)\ \ \text{NO!!} \end{align} $$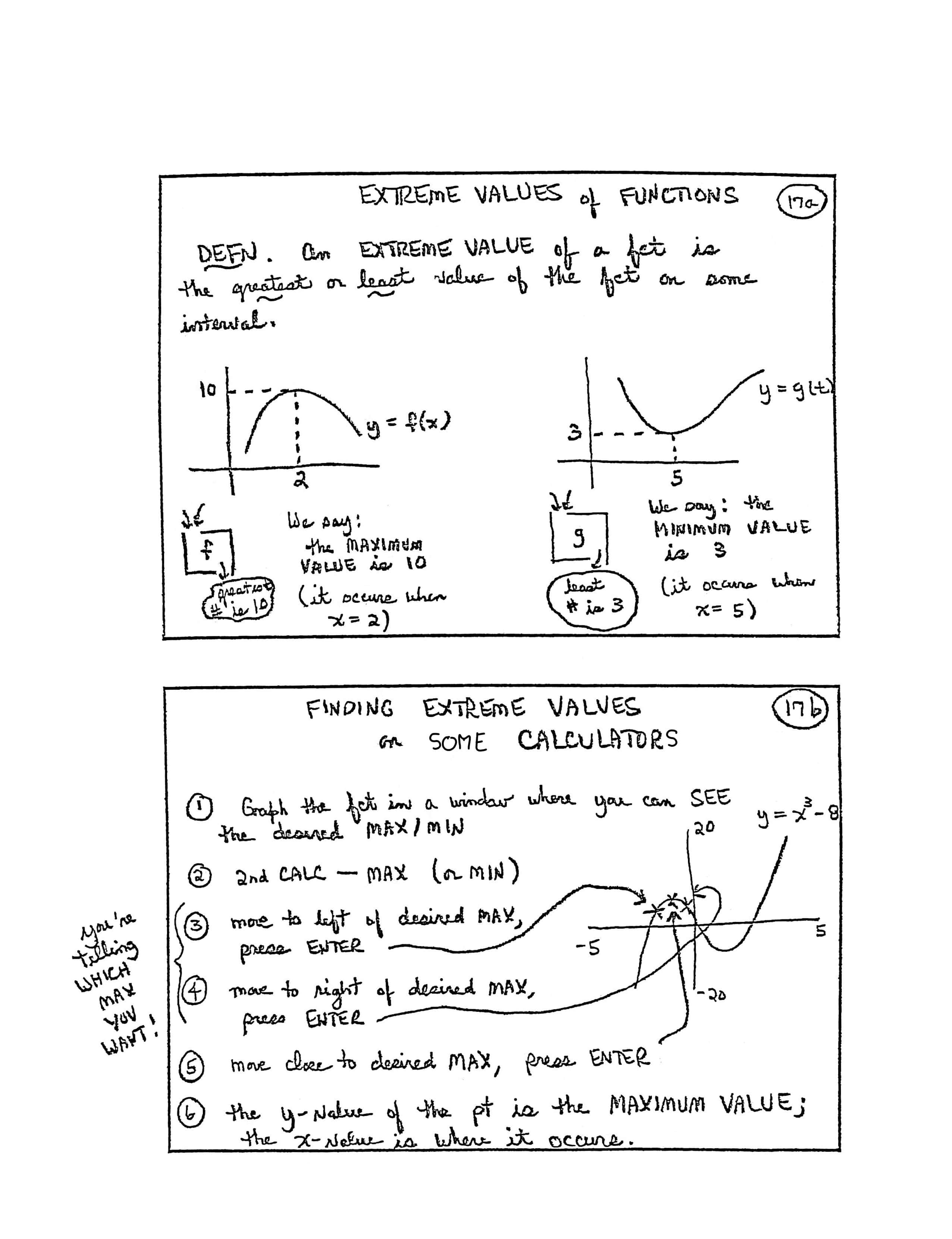
EXTREME VALUES of FUNCTIONS
DEFN. An EXTREME VALUE of a fct [function] is the greatest or least value of the fct on some interval.
[labels on left graph] point $\,(2,10)\,,$ $\,y = f(x)\,,$ numbers going into the $\,f\,$ box, greatest # is $\,10$
We say: the MAXIMUM VALUE is $\,10\,$ (it occurs when $\,x = 2\,$)
[labels on right graph] point $\,(5,3)\,,$ $\,y = g(t)\,,$ numbers going into the $\,g\,$ box, least # is $\,3$
We say: the MINIMUM VALUE is $\,3\,$ (it occurs when $\,x = 5\,$)
FINDING EXTREME VALUES ON SOME CALCULATORS
(1) Graph the fct in a window where you can SEE the desired MAX/MIN
(2) 2nd CALC — MAX (or MIN)
(3) Move to left of desired MAX, press ENTER
(4) Move to right of desired MAX, press ENTER
(For steps (3) and (4), you're telling WHICH MAX YOU WANT!)
(5) Move close to desired MAX, press ENTER
(6) The $y$-value of the pt [point] is the MAXIMUM VALUE; the $x$-value is where it occurs.
[labels on graph] $\,y = x^3 - 8\,,$ window is from $\,-5\,$ to $\,5\,$ on $x$-axis, from $\,-20\,$ to $\,20\,$ on $y$-axis
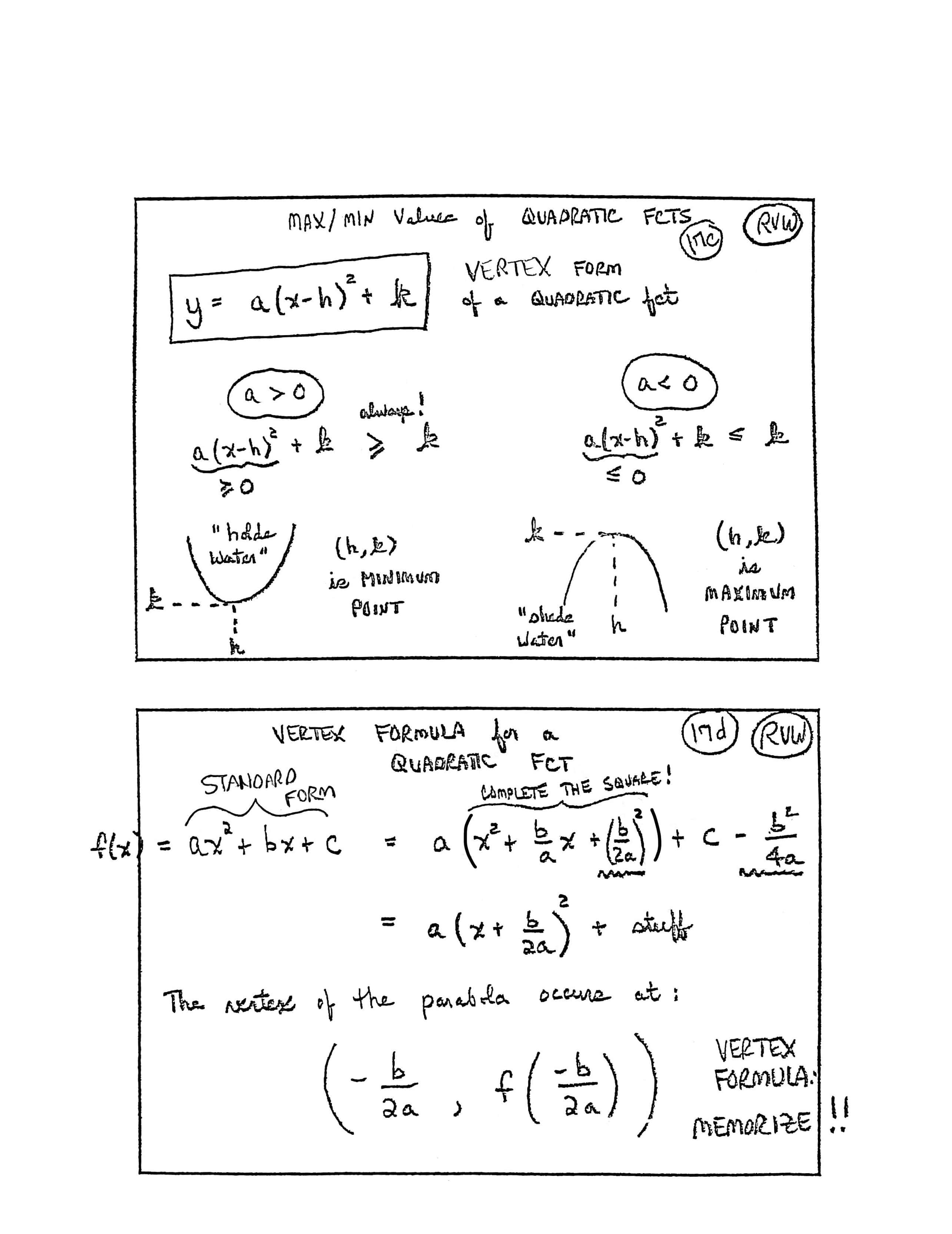
MAX/MIN VALUES OF QUADRATIC FCTS [functions]
$$ y = a(x-h)^2 + k $$VERTEX FORM of a QUADRATIC FCT
$$ \begin{gather} a \gt 0\cr \underbrace{a(x-h)^2}_{\ge 0} + k \overbrace{\ge}^{\text{always!}} k \end{gather} $$[labels on graph] point $\,(h,k)\,,$ “holds water”
$(h,k)\,$ is a MINIMUM POINT
$$ \begin{gather} a \lt 0\cr\cr \underbrace{a(x-h)^2}_{\le 0} + k \le k \end{gather} $$[labels on graph] point $\,(h,k)\,,$ “sheds water”
$(h,k)\,$ is a MAXIMUM POINT
VERTEX FORMULA for a QUADRATIC FCT
$$ \begin{align} f(x) &= \overbrace{ax^2 + bx + c}^{\text{standard form}}\cr\cr &= a \overbrace{\left(x^2 + \frac bax + \bigl(\frac b{2a}\bigr)^2\right)}^{\text{Complete the square!}} + c - \frac{b^2}{4a}\cr\cr &= a\bigl(x + \frac b{2a}\bigr)^2 + \text{stuff} \end{align} $$The vertex of the parabola occurs at:
$$ \left( -\frac b{2a}\,,\,f\bigl(-\frac{b}{2a}\bigr) \right) $$VERTEX FORMULA: MEMORIZE!!

INTERCEPTS of a QUADRATIC FCT [function]
$y$-INTERCEPT: Set $\,x = 0\,$; solve for $\,y$
$x$-INTERCEPTS: Set $\,y = 0\,$; solve for $\,x$
$$ \begin{gather} \text{(first column)}\cr y = ax^2+ bx + c\cr\cr \text{Use Quadratic Formula, if needed:}\cr\cr ax^2 + bx + c = 0\cr \text{iff}\cr x = \frac{-b\pm\sqrt{b^2-4ac}}{2a} \end{gather} $$ $$ \begin{gather} \text{(second column)}\cr y = a(x-h)^2 + k\cr\cr 0 = a(x-h)^2 + k\cr\cr \text{EX [example]}\cr\cr 0 = 2(x-1)^2 - 5\cr 5 = 2(x-1)^2\cr \frac 52 = (x-1)^2\cr x-1 = \pm\sqrt{\frac 52}\cr x = 1\pm \sqrt{\frac 52} \end{gather} $$PUTTING a QUADRATIC FCT in VERTEX FORM by COMPLETING THE SQUARE
$$ \begin{align} f(x) &= 5x^2 - 30x + 49\cr &= 5(x^2 - 6x\ \ \ \ \ \ \ ) + 49\cr &= 5(x^2 - 6x + 9) + 49 - 45\cr &\qquad \text{(Note: $(\frac{-6}2)^2 = 9\,$)}\cr &= 5(x-3)^2 + 4 \end{align} $$Vertex @ [at] $\,(3,4)\,$; holds water

MAX/MIN PROBLEMS
Sample: Among all rectangles that have a perimeter of $\,20\,$ ft, find the dimensions of the one with the largest area.
FIND FUNCTION TO BE MAXIMIZED; express it in terms of ONLY ONE VARIABLE.
$$ \begin{align} A(x) &= xy\cr &= x(10-x)\ \ \text{(from below)}\cr &= -x^2 + 10x \end{align} $$ $$ \begin{gather} 2x + 2y = 20\cr 2y = 20-2x\cr y = 10-x \end{gather} $$[graph] max point $\,(5,25)\,,$ $\,y = A(x)$
Using VERTEX FORMULA, max occus when $\,x = -\frac b{2a} = -\frac{10}{2(-1)} = 5\,$; $\,A(5) = 5(5) = 25\,.$
The dimensions are $\,5\text{ ft}\times 5\text{ ft}\,.$
MAX/MIN PROBLEMS
Sample: FIND $\,2\,$ positive #s [numbers] whose SUM is $\,100\,$ and the sum of whose squares is a MINIMUM.
Let $\,x,\,y\,$ be the two positive #s.
$$ \begin{gather} x + y = 100\cr y = 100-x \end{gather} $$ $$ \begin{align} \text{Sum of squares} &= x^2 + y^2\cr S(x) &= x^2 + (100-x)^2 \end{align} $$[graph] From CALCULATOR: minimum point $\,(50,5000)$
The #s are $\,50\,$ and $\,50\,.$
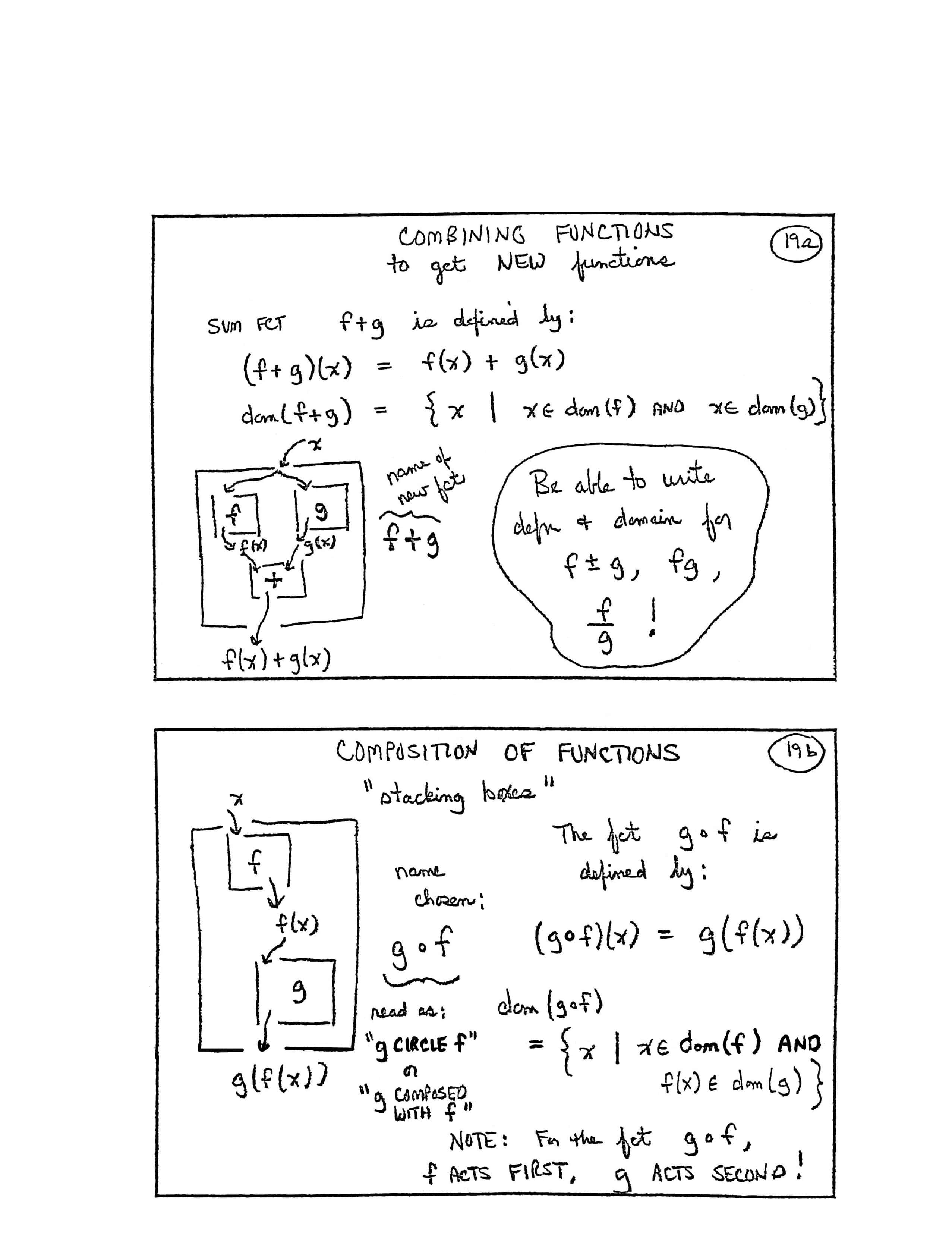
COMBINING FUNCTIONS to get NEW Functions
SUM FCT [function] $\,f+g\,$ is defined by:
$$ \begin{gather} (f+g)(x) = f(x) + g(x)\cr\cr \text{dom}(f+g) = \{ x\ |\ x\in\text{dom}(f) \text{ and } x\in\text{dom}(g)\} \end{gather} $$[image] $x\,$ goes into box labeled $\,f+g\,,$ (name of new fct), $\,f(x)\,$ comes out of $\,f\,$ box, $\,g(x)\,$ comes out of $\,g\,$ box, $\,f(x)\,$ and $\,g(x)\,$ are dropped into the ‘$\,+\,$’ box, $\,f(x) + g(x)\,$ comes out of bottom
Be able to write defn [definition] and domain for $\,f\pm g\,,$ $\,fg\,,$ $\,\frac fg\,$!
COMPOSITION OF FUNCTIONS
“stacking boxes”
The fct [function] $\,g\circ f\,$ is defined by:
$$ \begin{gather} (g\circ f)(x) = g\bigl(f(x)\bigr)\cr\cr \text{dom}(g\circ f) = \{x\ |\ x\in\text{dom}(f) \text{ and } f(x)\in\text{dom}(g)\} \end{gather} $$[image] $\,x\,$ goes into $\,f\,$ box, $\,f(x)\,$ comes out and is dropped into $\,g\,$ box, and $\,g\bigl(f(x)\bigr)\,$ comes out bottom; name chosen: $\,g\circ f\,,$ read as: “$g\,$ circle $\,f\,$” or “$g\,$ composed with $\,f\,$”
NOTE: For the fct $\,g\circ f\,,$ $\,f\,$ acts FIRST, $\,g\,$ acts SECOND!

PRACTICE WITH FUNCTION COMPOSITION
Let $\,f(x) = x^2 - 1\,$ and $\,g(x) = 2 - 3x\,.$ FIND $\,(f\circ g)(x)\,$ and $\,(g\circ f)(x)\,.$
$$ \begin{align} (f\circ g)(x) &= f(g(x))\cr &= f(2-3x)\cr &= (2-3x)^2 - 1\cr &= 4 - 12x + 9x^2 - 1 \end{align} $$Write a CMS [Complete Mathematical Sentence]!! Line up ‘$\,=\,$’ signs.
$$ \begin{align} (g\circ f)(x) &= g(f(x))\cr &= g(x^2-1)\cr &= 2 - 3(x^2-1)\cr &= 2 - 3x^2 + 3\cr &= -3x^2 + 5 \end{align} $$Is fct [function] composition commutative? NO!!
WRITING A FCT [function] as a COMPOSITION
Let $\,h(x) = 5(x-4)^3 - 7\,.$ Find fcts [functions] $\,f\,$ and $\,g\,$ such that $\,h(x) = (f\circ g)(x)\,.$
SOLN: [Solution]
$$ \begin{align} x&\overset{-4}{\longrightarrow} x-4\cr &\overset{\text{cube}}{\longrightarrow} (x-4)^3\cr &\overset{\times 5}{\longrightarrow} 5(x-4)^3\cr &\overset{- 7}{\longrightarrow} 5(x-4)^3 - 7 \end{align} $$[Let $\,g\,$ take the first two tasks] $\,g(x) = (x-4)^3$
[Let $\,f\,$ take the last two tasks] $\,f(x) = 5x-7$
Check:
$$ \begin{align} (f\circ g)(x) &= f(g(x))\cr &= f((x-4)^3)\cr &= 5(x-4)^3 - 7 \end{align} $$Find $\,2\,$ different sets of fcts [functions] $\,f\,$ and $\,g\,$ that work!!

When can we use a FUNCTION BOX BACKWARDS?
[image] function box, named “SQUARE”, the number $\,4\,$ goes in the bottom, coming out the top: $\,2\,$? $\,-2\,$?
[image] function box, named “CUBE” the number $\,8\,$ goes in the bottom, $\,2\,$ comes out the top
[graph] $\,y = x^2\,,$ showing the output $\,4\,$ going back to two inputs, $\,2\,$ and $\,-2$
[graph] Graph of $\,y = x^3\,,$ showing the output $\,8\,$ going back to the input $\,2\,$
ANS [answer]: When each OUTPUT has exactly one corresponding INPUT!
ONE-TO-ONE FUNCTIONS
DEFN [definition] A function $\,f\,$ is one-to-one (1-1) iff [if and only if] whenever $\,x\ne y\,$ (INPUTS are different), $\,f(x)\ne f(y)\,$ (the corresponding OUTPUTS are different).
The graph of a FUNCTION passes a VERTICAL LINE TEST, because each INPUT has exactly one OUTPUT.
The graph of a 1-1 FCT [function] also passes a HORIZONTAL LINE TEST, because each OUTPUT has exactly one INPUT!
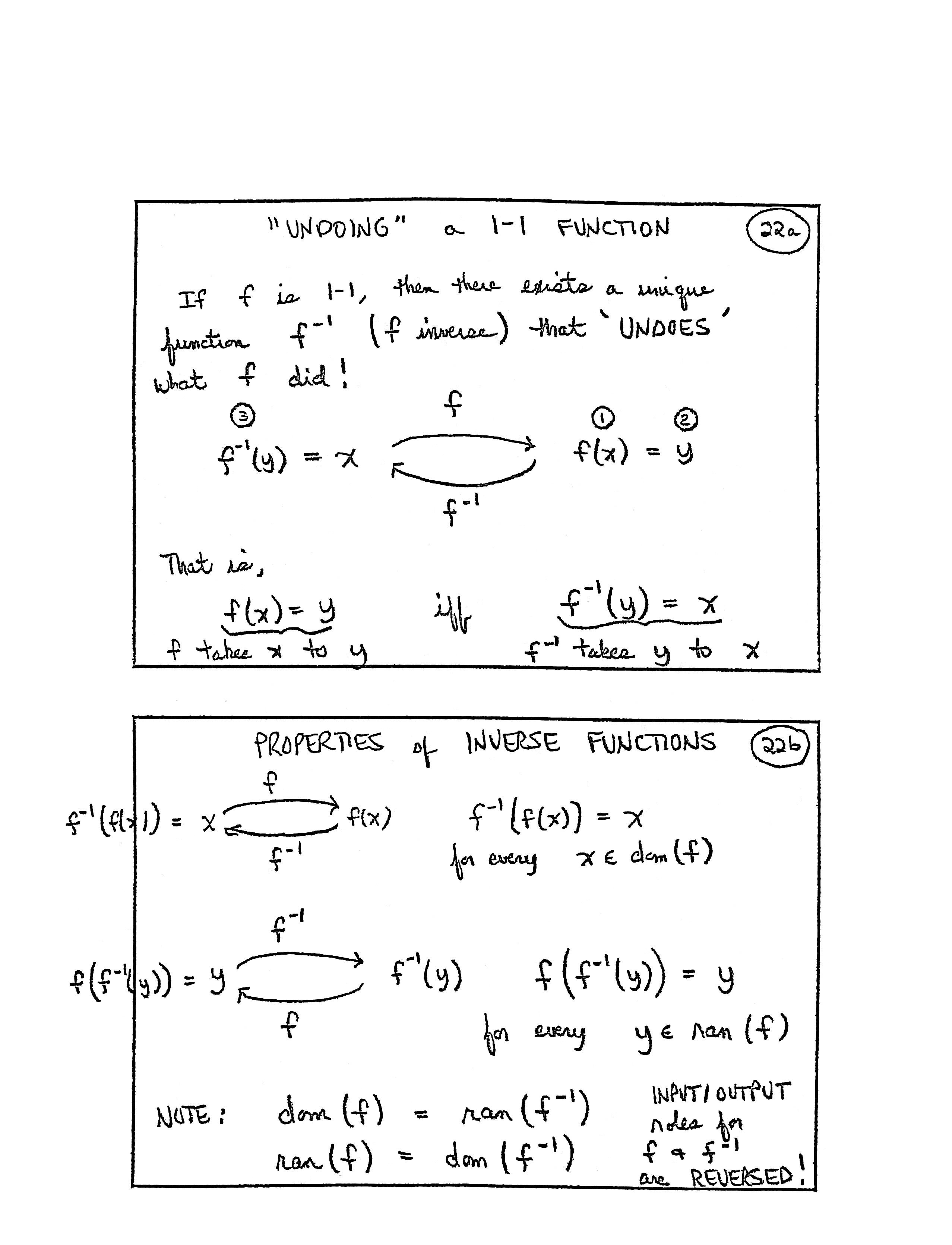
“UNDOING” a 1-1 FUNCTION
If $\,f\,$ is 1-1, then there exists a unique function $\,f^{-1}\,$ ($\,f\,$ inverse) that ‘UNDOES’ what $\,f\,$ did!
$$ \overset{(3)}{f^{-1}(y)} = x\quad \begin{matrix} \overset{f}{\longrightarrow} \cr \underset{\strut f^{-1}}{\longleftarrow} \end{matrix} \quad \overset{(1)}{\strut f(x)} = \overset{(2)}{\strut y} $$That is:
$$ \begin{gather} \underbrace{f(x) = y}_{\text{$f\,$ takes $\,x\,$ to $\,y$}}\cr\cr \text{iff [if and only if]}\cr\cr \underbrace{f^{-1}(y) = x}_{\text{$f^{-1}\,$ takes $\,y\,$ to $\,x$}}\cr\cr \end{gather} $$PROPERTIES of INVERSE FUNCTIONS
$$ f^{-1}\bigl(f(x)\bigr) = x\quad \begin{matrix} \overset{f}{\longrightarrow} \cr \underset{\strut f^{-1}}{\longleftarrow} \end{matrix} \quad f(x) $$$f^{-1}\bigl(f(x)\bigr) = x\,$ for every $\,x\in\text{dom}(f)$
$$ f\bigl(f^{-1}(y)\bigr) = y\quad \begin{matrix} \overset{f^{-1}}{\longrightarrow} \cr \underset{\strut f}{\longleftarrow} \end{matrix} \quad f^{-1}(y) $$$f\bigl(f^{-1}(y)\bigr) = y\,$ for every $\,y\in\text{ran}(f)$
NOTE:
$$ \begin{gather} \text{dom}(f) = \text{ran}(f^{-1})\cr \text{ran}(f) = \text{dom}(f^{-1}) \end{gather} $$INPUT/OUTPUT roles for $\,f\,$ and $\,f^{-1}\,$ are REVERSED!

Finding Inverse Functions (Switch Input/Output Names Method)
FINDING INVERSE FCTS [functions]
(when there's only one
‘$\,x\,$’
in the formula)
FIND the inverse:
$$ f(x) = 4 - \root 3\of{x+1} = -\root 3\of{x+1} + 4 $$[interpretation of mapping diagram]
- Start with: $\,x$
- Add $\,1\,$ to get: $\,x+1$
- Take the cube root to get: $\,\root 3\of{x+1}$
- Multiply by $\,-1\,$ to get: $\,-\root 3\of{x+1}$
- Add $\,4\,$ to get: $\,4 - \root 3\of{x+1}$
Now, UNDO these operations:
- Start with: $\,4 - \root 3\of{x+1}$
- Subtract $\,4\,$ to get: $\,-\root 3\of{x+1}$
- Multiply by $\,-1\,$ to get: $\,\root 3\of{x+1}$
- Cube to get: $\,x+1$
- Subtract $\,1\,$ to get: $\,x$
Check:
$$ \begin{align} f\bigl( f^{-1}(x) \bigr) &= f\bigl( (4-x)^3 - 1\bigr)\cr &= 4 - \root 3\of{(4-x)^3 - 1 + 1}\cr &= 4 - (4-x)\cr &= x \end{align} $$
FINDING INVERSE FCTS
(for more complicated formulas)
KEY IDEA: the INPUT/OUTPUT role for $\,f\,$ and $\,f^{-1}\,$ are reversed!
FIND the inverse: $\,f(x) = \frac{1-3x}{5 + 2x}$
- SIMPLIFY NOTATION; let $\,y = f(x)\,$: $\,y = \frac{1-3x}{5 + 2x}$
- Switch roles of $\,x\,$ and $\,y\,$: $\,x = \frac{1-3y}{5 + 2y}$
- Solve for $\,y\,$; rename as $\,f^{-1}(x)\,$:
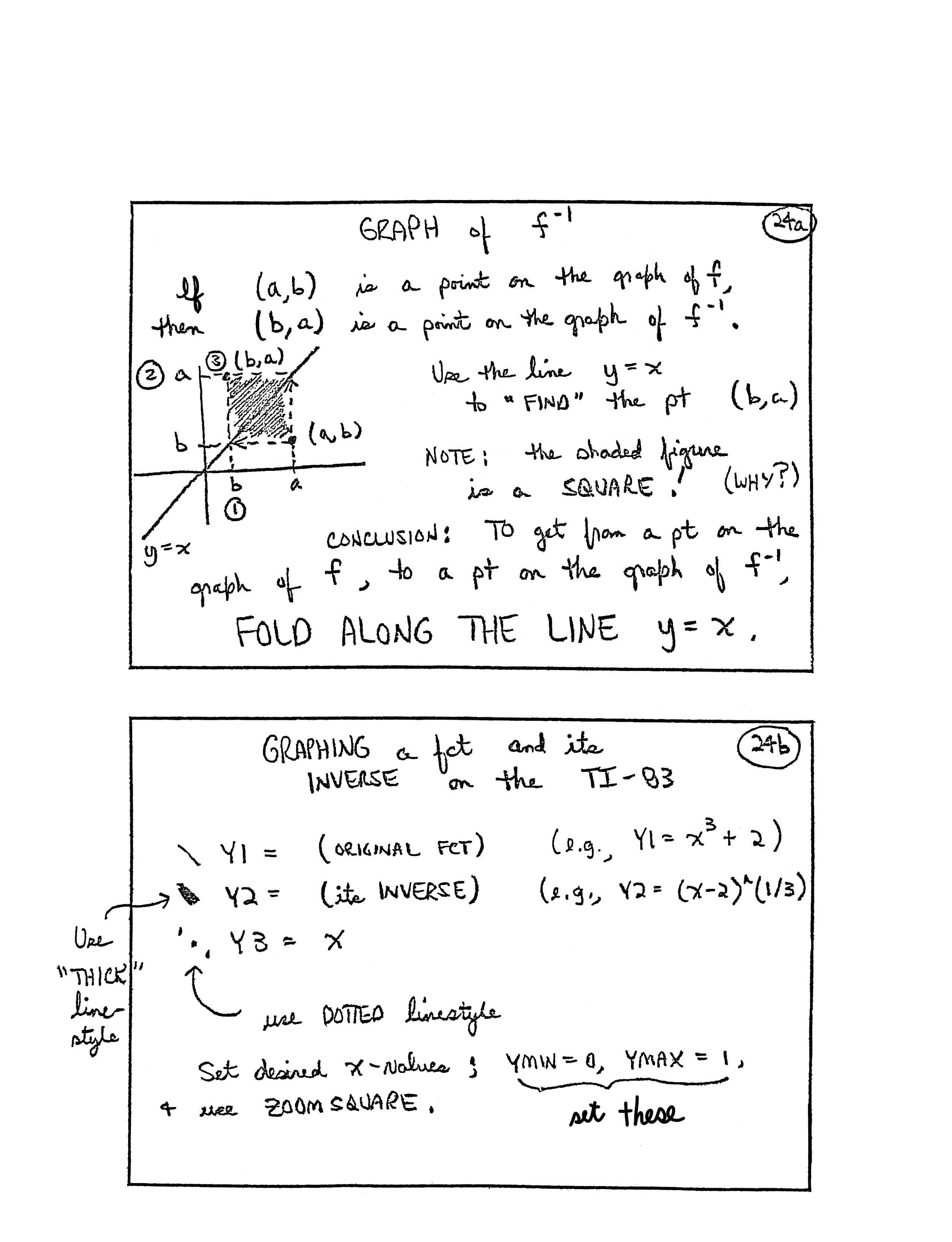
GRAPH of $\,f^{-1}$
If $\,(a,b)\,$ is a point on the graph of $\,f\,,$ then $\,(b,a)\,$ is a point on the graph of $\,f^{-1}\,.$
Use the line $\,y = x\,$ to “FIND” the pt [point] $\,(b,a)\,.$
[graph] Start with point $\,(a,b)\,.$ Draw an arrow horizontally to the line $\,y = x\,$ to locate $\,b\,$ on the $x$-axis (step 1). Then, draw an arrow from $\,(a,b)\,$ vertically to the line $\,y = x\,$ to locate $\,a\,$ on the $y$-axis (step 2). Finally, plot the point $\,(b,a)\,$ (step 3).
NOTE: the shaded figure in a SQUARE! (Why?)
CONCLUSION: To get from a pt on the graph of $\,f\,,$ to a pt on the graph of $\,f^{-1}\,,$ FOLD ALONG THE LINE $\,y = x\,.$
GRAPHING a fct [function] and its INVERSE on the TI-83
Y1 = (ORIGINAL FCT) (e.g., Y1 = x3 + 2) (use regular line-style)
Y2 = (its INVERSE) (e.g., Y2 = (x-2)^(1/3) (use “THICK” line-style)
Y3 = x (use DOTTED line-style)
Set desired $x$-values; YMIN = 0, YMAX = 1 (set these) and use ZOOMSQUARE.

POLYNOMIALS—terminology
DEFN [definition] A POLYNOMIAL is a sum of terms, each of the form $\,ax^n\,,$ where $\,a\in\Bbb R\,,$ and $\,n\in\{0,1,2,\ldots\}$
DEGREE of poly’l [polynomial]: the HIGHEST exponent
LEADING COEFFICIENT: the coefficient of the highest power term
EX [example] $$ P(x) = 2 - 3x^7 + \frac 43x^2 - \sqrt3\,x^4 $$
$4$ terms; degree $= 7\,$; leading coeff [coefficient] $= -3$
STANDARD FORM: (highest power 1st, walk on down)
$$ P(x) = -3x^7 - \sqrt 3\,x^4 + \frac 43x^2 + 2 $$ZEROS (ROOTS) of POLYNOMIALS
Let $\,P\,$ be a polynomial. The following are EQUIVALENT:
- $c\,$ is a zero (root) of $\,P$
- $P(c) = 0\,$ ($\,c\,$ is an INPUT whose OUTPUT is $\,0\,$)
- the graph of $\,P\,$ crosses the $x$-axis at $\,c\,$
- $x = c\,$ is a solution of the equation $\,P(x) = 0$
NOTE: These [first four] hold for ANY fct [function] $\,f$
- $x-c\,$ is a factor of $\,P(x)$
- $x-c\,$ goes into $\,P(x)\,$ evenly (remainder $= 0$)
- $P(x) = (x-c)(\text{stuff})$
These [last three] hold ONLY FOR POLYNOMIALS
EX [example]:
$2\,$ is a zero $\,\cdots\,$ $\,x-2\,$ is a factor
$-3\,$ is a zero $\,\cdots\,$ $\,x-(-3) = x+3\,$ is a factor
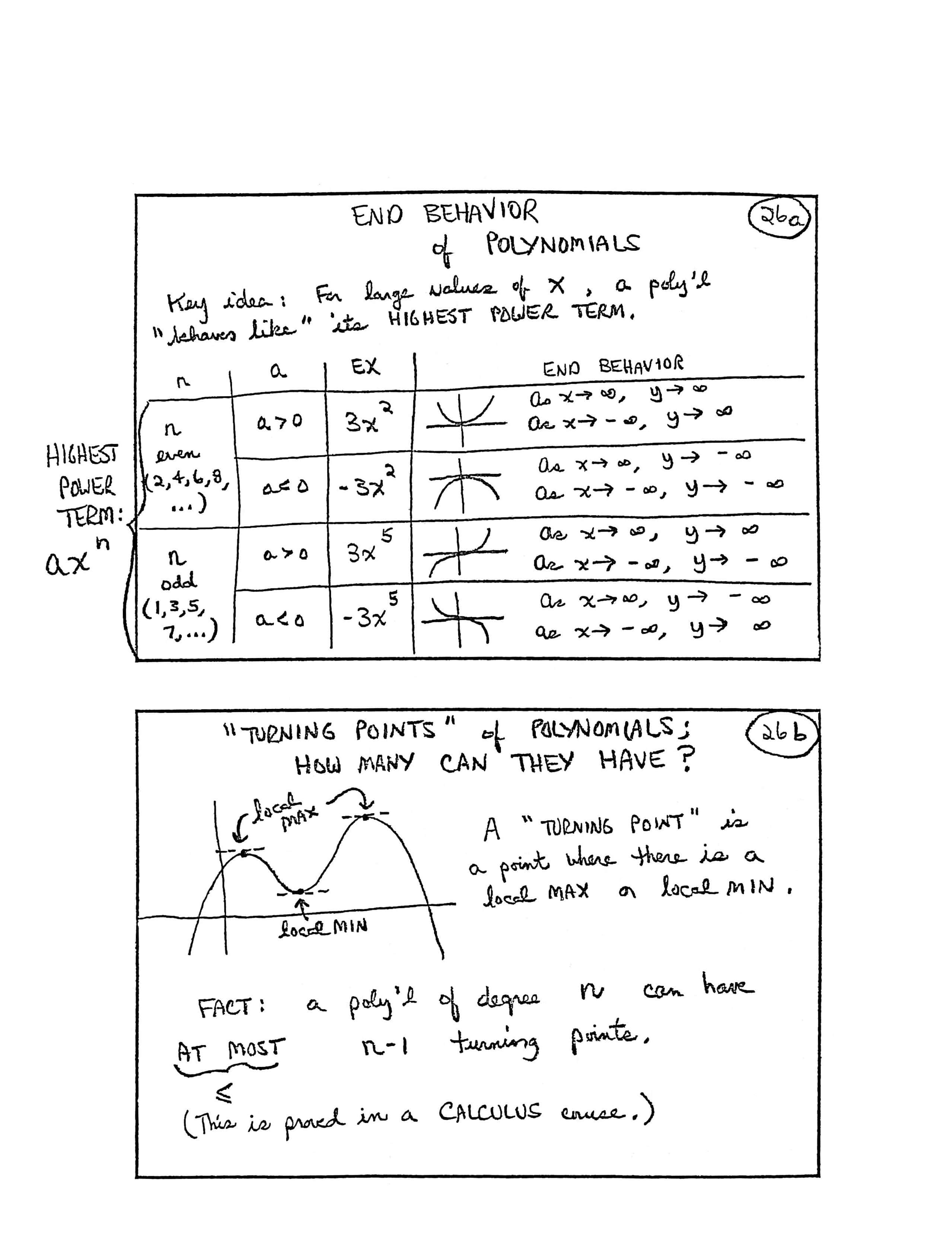
END BEHAVIOR of POLYNOMIALS
Key idea: For large values of $\,x\,,$ a poly’l [polynomial] “behaves like” its HIGHEST POWER TERM.
| $n$ | $a$ | EX [example] | END BEHAVIOR |
| $n\,$ even $(2,4,6,8,\ldots)$ | $a \gt 0$ | $3x^2$ |
As $\,x\rightarrow\infty\,,$ $y\rightarrow\infty$ As $\,x\rightarrow -\infty\,,$ $y\rightarrow\infty$ |
| $a\lt 0$ | $-3x^2$ |
As $\,x\rightarrow\infty\,,$ $y\rightarrow -\infty$ As $\,x\rightarrow -\infty\,,$ $y\rightarrow -\infty$ |
|
| $n\,$ odd $(1,3,5,7,\ldots)$ | $a \gt 0$ | $3x^5$ |
As $\,x\rightarrow\infty\,,$ $y\rightarrow\infty$ As $\,x\rightarrow -\infty\,,$ $y\rightarrow -\infty$ |
| $a\lt 0$ | $-3x^5$ |
As $\,x\rightarrow\infty\,,$ $y\rightarrow -\infty$ As $\,x\rightarrow -\infty\,,$ $y\rightarrow \infty$ |
“TURNING POINTS” of POLYNOMIALS; HOW MANY CAN THEY HAVE?
[graph] local MAX; local MIN
A “TURNING POINT” is a point where there is a local MAX [maximum] or a local MIN [minimum].
FACT: A poly’l of degree $\,n\,$ can have AT MOST (less than or equal to) $\,n-1\,$ turning points. (This is proved in a CALCULUS course.)

LONG DIVISION of POLYNOMIALS
EX [example]
$$ \frac{x^3 - 8x + 2}{x+3} \overbrace{=}^{\text{from below}} x^2 - 3x + 1 + \frac{-1}{x+3} $$SPOT-CHECK: EQUAL when $\,x = 0\,$?
[pieces of division problem]
[numerator, with $0$'s for MISSING TERMS]
$x^3 + 0x^2 - 8x + 2$
DIVISOR: $\,x+3$
QUOTIENT: $\,x^2 - 3x + 1$
[explanation] $(\frac{-3x^2}x = -3x)$
[explanation, after multiplying the $\,-3x\,$ by $\,x+3\,$] Put
in $\,(\,)\,$;
then SUBTRACT
REMAINDER: $\,-1\,$ (STOP when
$\,\text{deg}(\text{REM}) \lt \text{deg}(\text{DIVISOR})$
The DIVISION ALGORITHM
If $\,P(x)\,$ and $\,D(x)\,$ are polynomials with $\,D(x)\ne 0\,,$ then there exist unique poly's [polynomials] $\,Q(x)\,$ and $\,R(x)\,$ such that
$$ \frac{P(x)}{D(x)} = \overbrace{Q(x)}^{\text{QUOTIENT}} + \frac{\overbrace{R(x)}^{\text{REMAINDER}}}{\underbrace{D(x)}_{\text{DIVISOR}}} $$or, equivalently
$$P(x) = D(x)Q(x) + R(x)\,,$$where either
- $R(x) = 0\,$ (when $\,D(x)\,$ goes into $\,P(x)\,$ evenly); or
- $\text{deg}\bigl(R(x)\bigr) \lt \text{deg}\bigl(D(x)\bigr)$

“TRAPPING” the ROOTS of a POLYNOMIAL; the CONFINEMENT THEOREM
The polynomial equation
$$ a_nx^n + a_{n-1}x^{n-1} + \cdots + a_1x + x_0 = 0 $$has at most $\,n\,$ solutions in $\,\Bbb R\,,$ and they are contained in the interval $\,[-K,K]\,,$ where
$$ K = \frac{nM}{|a_n|} $$and where $\,M\,$ is the largest of $\,|a_n|\,,$ $\,|a_{n-1}|\,, \ldots, |a_0|\,.$
EX [example]: Find an interval that contains all the real solns [solutions] of:
$$ x^5 - x^4 + 2x^2 - 3x + 1 = 0 $$
ANS [answer]:
$\,n = 5\,,$ $\,a_n = 1\,,$
$\,M = 3\,,$ so
$\,K = \frac{5\cdot 3}1 = 15\,.$
INTERVAL: $\,[-15,15]$
APPROXIMATING SOLUTIONS to POLYNOMIAL EQS [equations] on your CALCULATOR
Solve: $\,P(x) = 0$
-
Graph $\,P(x)\,$
on the window specified by the CONFINEMENT
THM [theorem]; use (say)
YMIN = -20,YMAX = 20. AdjustXMIN, XMAXfor a better view, if needed. -
Use
CALC-ZEROto estimate zeros. -
Use
ZOOM-BOXfor a closer view, where needed.
HINT: If Calc-Zero doesn't work
in this situation, use Calc-MIN
instead!

COMPLEX NUMBERS
A COMPLEX # [number] is an expression of the form
$$a + bi$$where $\,a\,$ (REAL part of the complex #) and $\,b\,$ (IMAGINARY part of the complex #) are real #s [numbers], and $\,\overbrace{i^2 = -1}^{i = \sqrt{-1}}\,.$
[graph] point $\,1 + 2i\,$ is over $\,1\,$ and up $\,2\,$ in the COMPLEX PLANE; point $\,-2-i\,$ is to the left $\,2\,$ and down $\,1$
A PURE IMAGINARY # has real part equal to $\,0\,$: like $\,7i$
A REAL # has imaginary part equal to $\,0\,$: like $\,5$
EX [example] $\,3-4i\,$: real part $\,= 3\,$ and imaginary part $\,= -4$
ARITHMETIC WITH COMPLEX #s [numbers]
ADDITION: $\,(a + bi) + (c + di) = (a+c) + (b+d)i$
Verbalize: To add $\,2\,$ complex #s, add the real parts and add the
imaginary parts
EX [example] $\,(1-3i) + (4 + 5i) = 5 + 2i$
SUBTRACTION:
$$ \begin{align} (a+bi) - (c+di) &= a + bi - c - di\cr\cr &= (a-c) + (b-d)i \end{align} $$MULTIPLICATION:
$$ \begin{align} (a+bi)(c+di) &= ac + adi + bci + \overbrace{bdi^2}^{= -bd}\cr\cr &= (ac - bd) + (ad + bc)i \end{align} $$Don't memorize formula! Multiply out as needed.
DIVISION:
$$ \frac{a+bi}{c+di} = \frac{a+bi}{c+di}\cdot\frac{c-di}{c-di}\ \ \text{ and simplify!!} $$NOTE: The COMPLEX CONJUGATE of $\,c + di\,$ is $\,c - di$
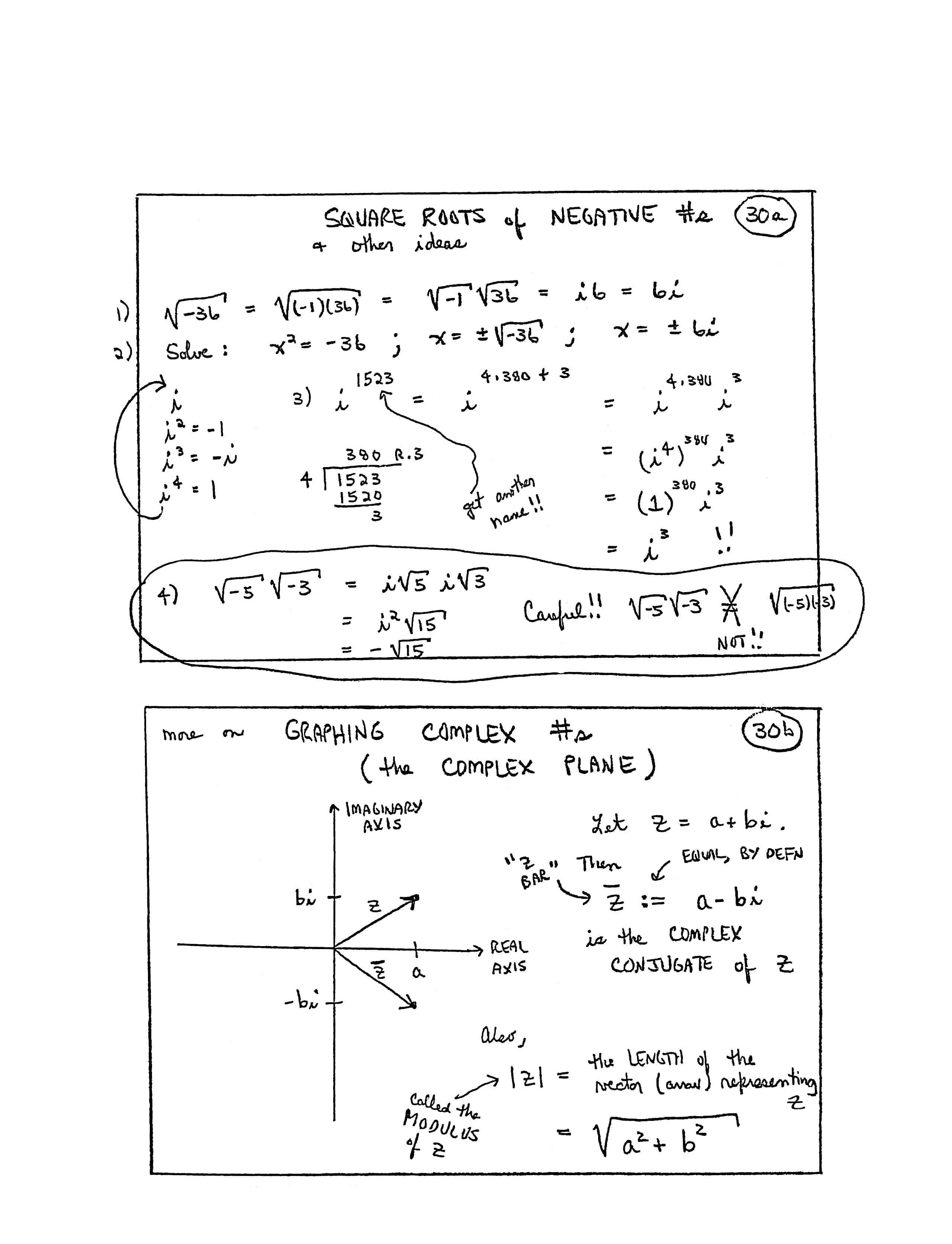
SQUARE ROOTS of NEGATIVE #s [numbers] & other ideas
(1)
$$ \begin{align} \sqrt{-36} &= \sqrt{(-1)(36)} = \sqrt{-1}\sqrt{36}\cr &= i6 = 6i \end{align} $$(2) Solve: $\,x^2 = -36\,$; $\,x = \pm\sqrt{-36}\,$; $\,x = \pm 6i$
$$ \begin{gather} i\cr i^2 = -1\cr i^3 = -i\cr i^4 = 1 \end{gather} $$(3)
$$ \begin{align} i^{\overbrace{1523}^{\substack{\text{get}\\ \text{another}\\ \text{name}}}} &= i^{\,4\cdot 380 + 3}\cr &= i^{\,4\cdot 380}\,i^3\cr &= (i^4)^{380}\, i^3\cr &= (1)^{380}\,i^3\cr &= i^3 \end{align} $$[division problem] Divide $\,1523\,$ by $\,4\,$; it goes in $\,380\,$ times, with a remainder of $\,3$
(4)
$$ \begin{align} \sqrt{-5}\sqrt{-3} &= i\sqrt{5}\ i\sqrt{3}\cr &= i^2\sqrt{15}\cr &= -\sqrt{15} \end{align} $$Careful!!
$$ \sqrt{-5}\,\sqrt{-3} \overbrace{\ne}^{\text{is NOT equal to!}} \sqrt{(-5)(-3)} $$more on GRAPHING COMPLEX #s (the COMPLEX PLANE)
[graph] vertical axis is the IMAGINARY AXIS; horizontal axis is the REAL AXIS; labels $\,bi\,$ and $\,-bi\,$ on the imaginary axis; label $\,a\,$ on real axis; $\,z = a+bi\,$ and $\,\bar z = a - bi$
Let $\,z = a + bi\,.$ Then
$$ \overbrace{\bar z}^{\text{“$z$ bar”}} \overbrace{:=}^{\text{equal, by defn}} a - bi $$is the COMPLEX CONJUGATE of $\,z\,.$
Also,
$$ \begin{align} &\overbrace{|z|}^{\substack{\text{called the}\\ \text{MODULUS of $\,z$}}}\cr\cr &\quad = {\small\text{the LENGTH of the vector}}\cr &\qquad \ \ {\small\text{(arrow) representing $\,z$}}\cr\cr &\quad = \sqrt{a^2 + b^2} \end{align} $$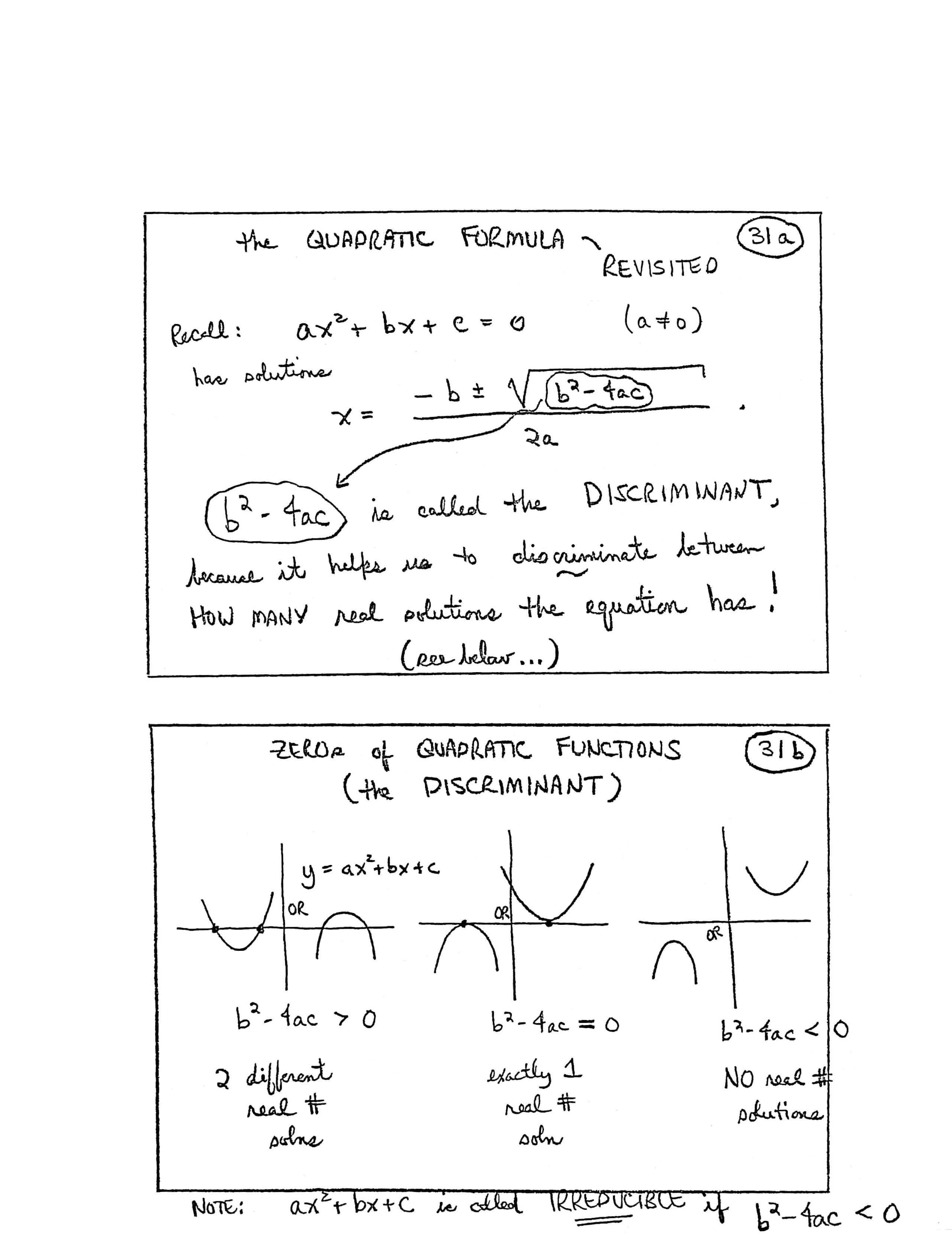
the QUADRATIC FORMULA—REVISITED
Recall: $\,ax^2 + bx + c = 0\,$ ($\,a\ne 0\,$) has solutions:
$$ x = \frac{-b\pm\sqrt{b^2-4ac}}{2a} $$$b^2 - 4ac\,$ is called the DISCRIMINANT, because it helps us to discriminate between HOW MANY real solutions the equation has! (See below...)
ZEROs of QUADRATIC FUNCTIONS (the DISCRIMINANT)
[graphs] $\,y = ax^2 + bx + c$
First graph: $\,b^2 - 4ac\gt 0\,,$ $\,2\,$ different real # [number] solns [solutions]
Second graph: $\,b^2 - 4ac = 0\,,$ exactly $\,1\,$ real # soln
Third graph: $\,b^2 - 4ac \lt 0\,,$ NO real # solutions
NOTE: $\,ax^2 + bx + c\,$ is called IRREDUCIBLE if $\,b^2 - 4ac\lt 0$

MULTIPLICITY of a ZERO
Let $\,P(x)\,$ be a polynomial.
DEFN [definition]
| $c\,$ is a zero of multiplicity $\,k$ | iff [if and only if] | $x-c\,$ is a factor EXACTLY $\,k\,$ times |
EXAMPLE:
$$ \begin{align} P(x) &= 7x^5(x-1)^3(2x-3)^4(x+5)\cr &= 7x^5(x-1)^3\cdot 2^4(x-\frac 32)^4(x+5)\ \ \text{(How?)} \end{align} $$| zero | multiplicity |
| $0$ | $5$ |
| $1$ | $3$ |
| $\frac 32$ | $4$ |
| $-5$ | $1$ (a zero of multiplicity $\,1\,$ is called a SIMPLE ZERO) |
MULTIPLICITY OF ZEROS: GRAPHICAL CONSEQUENCES
| $P(x) =$ | GRAPH NEAR $\,c$ | |
| $(x-c)(\text{other stuff})$ | [graph] OR [graph] | Cuts straight through! |
| $\underbrace{(x-c)^2}_{\text{always }\gt\, 0}(\text{stuff})$ | [graph] OR [graph] | EVEN POWERS: NO SIGN CHANGE |
| $\underbrace{(x-c)^3}_{\substack{x\,\gt\, c:\, +\cr x\,\lt\,c:\,-}}(\text{stuff})$ | [graph] OR [graph] | ODD POWERS: SIGN CHANGE |
| $x$ | $(x-3)^2$ | $(x-3)^4$ | $(x-3)^6$ |
| $3.1$ | $0.01$ | $0.0001$ | $0.000001$ |
GRAPH gets FLATTER near $\,c\,$ as MULTIPLICITY INCREASES!

the FUNDAMENTAL THEOREM OF ALGEBRA
NOTE: $\,\Bbb C = \,$ the set of COMPLEX #s [numbers]
Consequence: Every poly'l [polynomial] of degree $\,n\,$ with complex coeffs [coefficients] has EXACTLY $\,n\,$ zeros in $\,\Bbb C\,$ (counting multiplicities). (WHY is this a consequence?)
POLYNOMIALS with REAL # COEFFICIENTS
Spse [suppose] that $\,P(x)\,$ has REAL # coefficients.
- If $\,a + bi\,$ ($\,b\ne 0\,$) is a zero, then so is $\,a - bi\,$ (i.e., NON-REAL zeros must occur in complex conjugate pairs).
- $$ \begin{align} &\bigl(x - (a+bi)\bigr)\bigl(x-(a-bi)\bigr)\cr\cr &\quad \overset{\text{Check!}}{=} \underbrace{x^2 - 2ax + (a^2 + b^2)}_{\text{irreducible quadratic}} \end{align} $$
- $P(x)\,$ can be factored into LINEAR FACTORS and IRREDUCIBLE QUADRATICS

SOLVING POLYNOMIAL EQUATIONS
degree $\,\le 2\,$: NO PROBLEM!!
EXAMPLE: SOLVE
$$x^5 - 2 = 2x^3 + 2x^2 + 3x$$(Find ALL complex # [number] solutions, if possible.)
STEP 1: Write in form $\,P(x) = 0$
$$ \underbrace{x^5 - 2x^3 - 2x^2 - 3x - 2}_{P(x)} = 0 $$STEP 2: GRAPH $\,P\,$: use Confinement Thm [theorem]; read off any real zeros
STEP 3: Use long division, as needed, to completely factor $\,P\,.$
(FINISH the problem on card 34a!)
Should get these solutions:
$$ \begin{align} &x^5 - 2x^3 - 2x^2 - 3x - 2\cr &\quad = (x+1)^2(x-2)(x^2 + 1)\cr &\quad = 0 \end{align} $$SOLNS [solutions]: $\{\underbrace{-1}_{\text{MULT } 2},\, 2,\, \pm i\}$

RATIONAL FCTS [functions]
EX [example] $\displaystyle\,y = \frac{x-1}{x-2}$
[graph] The line $\,y = 1\,$ is the HORIZONTAL ASYMPTOTE; the line $\,x = 1\,$ is the VERTICAL ASYMPTOTE
DOMAIN: $\,\{x\ |\ \text{denominator} \ne 0\}$
$y$-INTERCEPT: set $\,x = 0$
$x$-INTERCEPT: set $\,\text{NUM [numerator]} = 0$
(WHY? The only way a FRACTION can equal zero, is if the NUMERATOR equals zero)
ASYMPTOTES
An ASYMPTOTE is a curve (usually a line) that another curve gets arbitrarily close to as $\,x\,$ approaches $\,+\infty\,,$ $\,-\infty\,,$ or some finite # [number].
[dashed vertical line $\,x = 2\,$] $\,x=2\,$ is a VERTICAL ASY [asymptote]:
$$ \begin{gather} \text{as} \ \underbrace{x\rightarrow 2^+}_{\text{“}\,x\,\text{approaches}\, 2\,\text{from the right”}}\,,\ y\rightarrow +\infty\cr \cr \text{as}\ x\rightarrow 2^-\,, y\rightarrow -\infty \end{gather} $$[dashed horizontal line $\,y = 1\,$] $\,y = 1\,$ is a HORIZ ASY [asymptote]:
$$ \begin{gather} \text{as}\ x\rightarrow \infty\,,\ y\rightarrow 1 \cr\cr \text{as}\ x\rightarrow -\infty\,,\ y\rightarrow 1 \end{gather} $$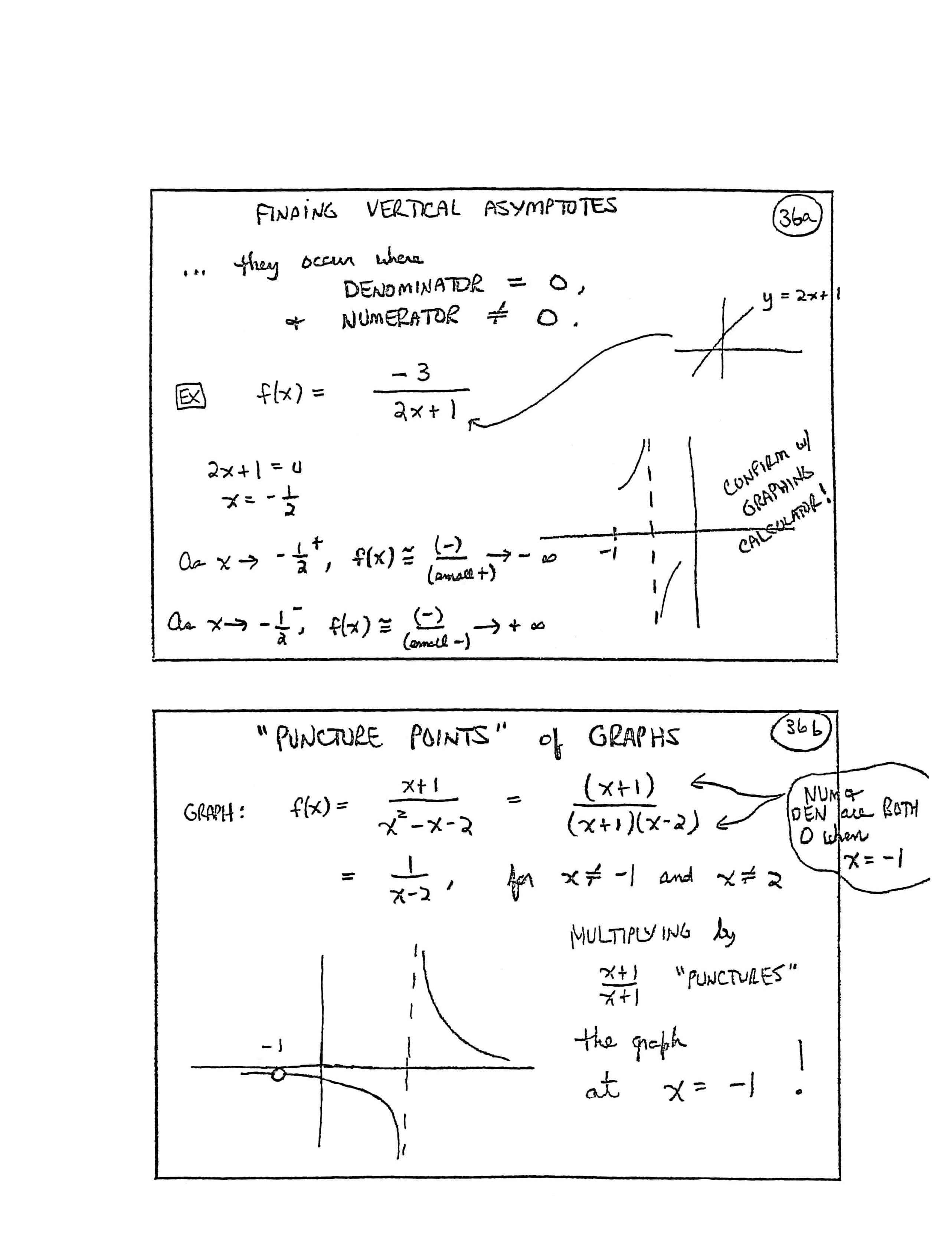
Introduction to Puncture Points (Holes)
Finding ‘Puncture Points’ of Graphs
FINDING VERTICAL ASYMPTOTES
... they occur where:
$$ \begin{gather} \text{DENOMINATOR} = 0\,,\cr \text{and}\ \ \text{NUMERATOR} \ne 0 \end{gather} $$EX [example]
$$f(x) = \frac{-3}{2x+1}$$[graph] Graph $\,y = 2x+1\,,$ which is zero at $\,-\frac 12\,,$ negative to the left of $\,-\frac12\,,$ and positive to the right of $\,-\frac 12\,.$
$$ \begin{gather} 2x + 1 = 0\cr x = -\frac 12 \end{gather} $$As $\,x\rightarrow -\frac 12^+\,,$ $\,f(x)\approx \frac{(-)}{(\text{small}\, +)} \rightarrow -\infty$
As $\,x\rightarrow -\frac 12^-\,,$ $\,f(x)\approx \frac{(-)}{(\text{small}\, -)} \rightarrow +\infty$
[graph of $\,y = \frac{-3}{2x+1}\,,$ showing vertical asymptote at $\,x = -\frac 12\,$] Confirm w/ [with] graphing calculator!
“PUNCTURE POINTS” of GRAPHS
GRAPH:
$$ \begin{align} f(x) &= \frac{x+1}{x^2 - x - 2}\cr\cr &= \frac{(x+1)}{(x+1)(x-2)}\cr &\quad \text{(NUM & DEN are both $\,0\,$ when $\,x=-1\,$)}\cr\cr &= \frac{1}{x-2}\,,\ \ \text{for}\ x\ne -1\ \text{and}\ x\ne 2 \end{align} $$[NUM = numerator; DEN = denominator]
Multiplying by $\,\frac{x+1}{x+1}\,$ “punctures” the graph at $\,x = -1\,$!
[graph of $\,y = \frac{x+1}{x^2 - x - 2}\,,$ showing puncture point at $\,x = -1\,$ and vertical asymptote at $\,x = 2\,$]

FINDING HORIZONTAL ASYMPTOTES
Let $\,R(x) = \frac{N(x)}{D(x)}\,.$
$\text{deg}\, N(x) \lt \text{deg}\, D(x)\,$;
EX [example]: $\,R(x) = \frac{3x-1}{5x^2 + 2x - 1}\,$;
denominator gets bigger faster than numerator;
as $\,x\rightarrow \pm\infty\,,$
$\,y\rightarrow 0\,$;
$\,y = 0\,$ is a HORIZONTAL ASYMPTOTE.
$\text{deg}\, N(x) = \text{deg}\, D(x)\,$;
EX:
$$ \begin{align} R(x) &= \frac{3x-1}{5x + 2}\cdot\frac{\frac1x}{\frac1x}\cr &= \frac{3 - \frac 1x}{5 + \frac 2x} \end{align} $$
NUM [numerator] and DENOM [denominator] “grow”
at same rate;
as $\,x\rightarrow \pm\infty\,,$
$\,y\,$ looks like ratio of leading terms;
$\,y = \frac{\text{leading coeff [coefficient] of $\,N(x)$}}
{\text{leading coeff of $\,D(x)$}}\,$
is HORIZ ASY [horizontal asymptote].
FINDING SLANT ASYMPTOTES
If degree of NUMERATOR is exactly $\,1\,$ more than degree of DENOMINATOR ($\,\text{deg}\,N(x) = 1 + \text{deg}\,D(x)\,$) then you have a SLANT ASYMPTOTE. Do a LONG DIVISION!
$$ \begin{align} R(x) &= \frac{x^2 - 4x - 5}{x-3} \cr &= x-1 + \frac{-8}{x-3} \end{align} $$[long division, showing $\,x^2 - 4x - 5\,$ being divided by $\,x-3\,,$ getting a quotient of $\,x-1\,$ with a remainder of $\,-8\,$]
As $\,x\rightarrow \pm\infty\,,$ $\,\frac{-8}{x-3}\rightarrow 0\,.$
$\,y = x-1\,$ is a SLANT ASYMPTOTE.
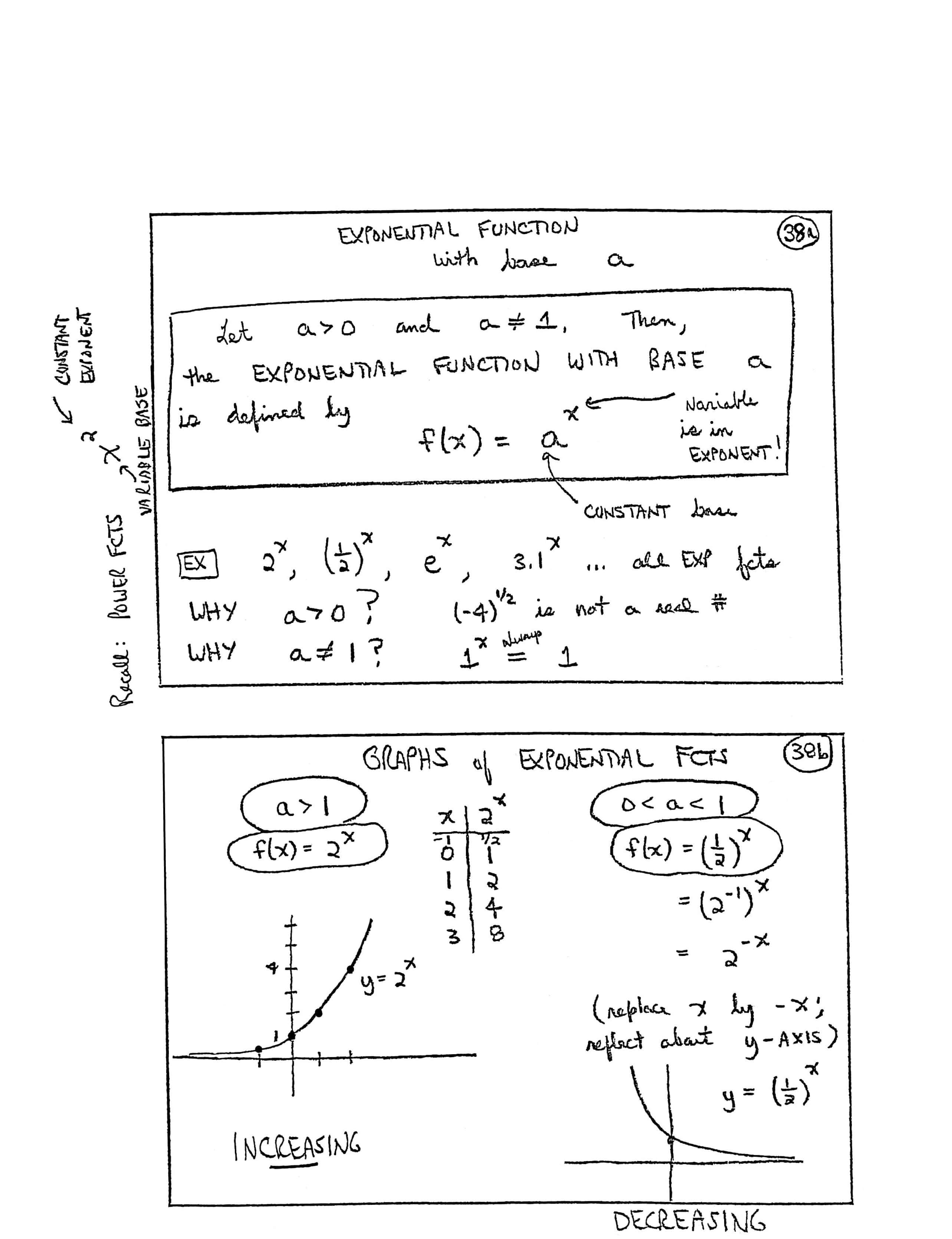
EXPONENTIAL FUNCTION with base $\,a$
EX [example]: $\,2^x\,,$ $\,(\frac 12)^x\,,$ $\,\text{e}^x\,,$ $\,3.1^x\,$ ... all EXP [exponential] fcts [functions].
WHY $\,a\gt 0\,$? $\,(-4)^{1/2}\,$ is not a real #
WHY $\,a\ne 1\,$? $\,1^x \overset{\text{always}}{=} 1$
GRAPHS of EXPONENTIAL FCTS [functions]
$\,a\gt 1\,,$ $\,f(x) = 2^x$
| $x$ | $2^x$ |
| $-1$ | $\frac 12$ |
| $0$ | $1$ |
| $1$ | $2$ |
| $2$ | $4$ |
| $3$ | $8$ |
[graph] plotted points $\,(-1,\frac 12)\,,$ $\,(0,1)\,,$ $\,(1,2)\,,$ graph is labeled $\,y = 2^x\,,$ INCREASING
$0\lt a\lt 1$
$$ \begin{align} f(x) &= (\frac 12)^x\cr &= (2^{-1})^x\cr &= 2^{-x} \end{align} $$(Replace $\,x\,$ by $\,-x\,$; reflect about $y$-axis)
[graph] $y = (\frac 12)^x\,,$ DECREASING
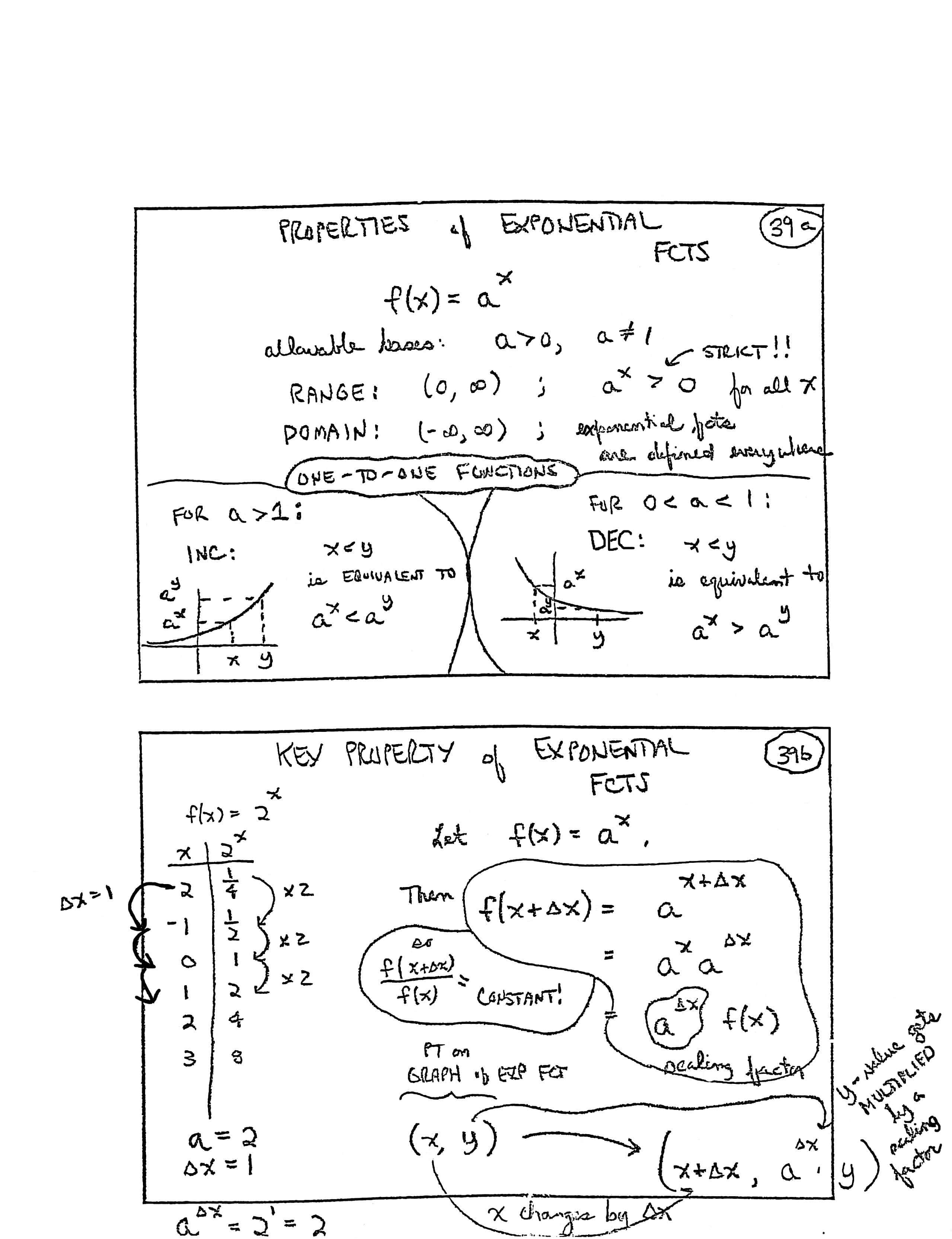
PROPERTIES OF EXPONENTIAL FCTS [functions]
$$f(x) = a^x$$allowable bases: $\,a\gt 0\,, a\ne 1$
RANGE: $\,(0,\infty)\,$: $\,a^x \overset{\text{Strict!!}}{\gt} 0\,$ for all $\,x$
DOMAIN: $\,(-\infty,\infty)\,$; exponential fcts are defined everywhere
ONE-TO-ONE FUNCTIONS
For $\,a\gt 1\,,$ INC [increasing]: $\,x\lt y\,$ is equivalent to $\,a^x \lt a^y$
For $\,0 \lt a \lt 1\,,$ DEC [decreasing]: $\,x\lt y\,$ is equivalent to $\,a^x \gt a^y$
KEY PROPERTY OF EXPONENTIAL FCTS [functions]
Let $\,f(x) = a^x\,.$ Then:
$$ \begin{align} f(x+\Delta x) &= a^{x+\Delta x}\cr\cr &= a^x\,a^{\Delta x}\cr\cr &= \underbrace{a^{\Delta x}}_{\text{scaling factor}}\cdot f(x) \end{align} $$so
$$ \frac{f(x+\Delta x)}{f(x)} = \text{CONSTANT!} $$ $$ \overbrace{(x,y)}^{\substack{\text{pt on}\cr \text{graph of}\cr \text{exp fct}}} \rightarrow \bigl( \overbrace{x+\Delta x}^{\text{$x\,$ changes by $\,\Delta x$}}\,,\, \underbrace{a^{\Delta x}\cdot y}_{\substack{ \text{$y$-value}\cr \text{gets multiplied}\cr \text{by a}\cr \text{scaling factor}}} \bigr) $$| $f(x) = 2^x$ | |
| $x$ | $2^x$ |
| $2$ | $\frac 14$ |
| $-1$ | $\frac 12$ |
| $0$ | $1$ |
| $1$ | $2$ |
| $2$ | $4$ |
| $3$ | $8$ |
|
$a = 2$ $\Delta x = 1$ $a^{\Delta x} = 2^1 = 2$ |
|
[Note: In this table, note that as the $x$-values successively increase by $\,1\,$ ($\,\Delta x = 1\,$), the $y$-values get successively multiplied by the scaling constant $\,2\,.$]

LINEAR versus EXPONENTIAL FCTS [functions]
FIND equal changes in $\,x\,$; how does $\,y\,$ change?
Be able to RECOGNIZE lin/exp [linear/exponential] fcts [functions] from a table, and FIND A FORMULA!
| $x$ | $f(x)$ |
| $-2$ | $\frac 29$ |
| $0$ | $2$ |
| $2$ | $18$ |
| $4$ | $162$ |
| EXPONENTIAL! | |
[Note the equal changes in $\,x\,$:]
- from $\,-2\,$ to $\,0\,$ is $\,\color{red}{2}$
- from $\,0\,$ to $\,2\,$ is $\,\color{red}{2}$
- from $\,2\,$ to $\,4\,$ is $\,\color{red}{2}$
[Also note that the $y$-values successively get multiplied by $\,9\,$:]
- $\frac 29\,$ times $\,\color{red}{9}\,$ gives $\,2$
- $2\,$ times $\,\color{red}{9}\,$ gives $\,18$
- $18\,$ times $\,\color{red}{9}\,$ gives $\,162$
| $x$ | $g(x)$ |
| $-2$ | $-5$ |
| $-1$ | $-1$ |
| $0$ | $3$ |
| $1$ | $7$ |
| $2$ | $11$ |
| LINEAR! | |
[Note the equal changes in $\,x\,$: the $x$-values keep increasing by $\,1\,.$ Also note the equal changes in $\,y\,$: the $y$-values keep increasing by $\,4\,$, so that $\,\Delta y = 4\,.$]
[On side of cards:]
$$ g(x) = mx + b $$ $$ \begin{align} g(x + \Delta x) &= m(x + \Delta x) + b\cr &= mx + m\Delta x + b\cr &= (mx + b) + m\Delta x\cr &= g(x) + m\Delta x \end{align} $$For linear fcts: equal changes in $\,x\,$ give rise to equal changes in $\,y\,.$
FINDING the FORMULA ...
$$ \begin{gather} \text{[for the exponential function]}\cr f(x) = K\cdot a^x\cr \text{(Find $\,K\,$ and $\,a\,$)}\cr\cr 18 = K\cdot a^2\cr 2 = K\cdot a^0\,\text{; so } K = 2\cr\cr 18 = 2\cdot a^2\cr 9 = a^2\cr a = 3\cr\cr f(x) = 2\cdot 3^x \text{ and check!!} \end{gather} $$$$ \begin{gather} \text{[for the linear function]}\cr g(x) = mx + b\cr \text{(Find $\,m\,$ and $\,b\,$)}\cr\cr m = \frac{7-3}{1-0} = 4\cr\cr 3 = 4(0) + b\cr b = 3\cr\cr g(x) = 4x + 3\text{ and check!!} \end{gather} $$

Introduction to Average Rate of Change
Introduction to Instantaneous Rate of Change and Tangent Lines
A Special Property of the Natural Exponential Function
the NATURAL EXPONENTIAL FUNCTION
... is the function $\,f(x) = {\text{e}}^x\,$ where the base $\,\text{e}\,$ is the IRRATIONAL # [number] defined by:
$$ \text{e} = \underbrace{\lim_{n\rightarrow\infty}}_{\substack{\text{the limit,}\cr \text{as $\,n\,$ goes}\cr \text{to infinity}} } \bigl(1+\frac 1n\bigr)^n \approx 2.72 $$| $n$ | $\bigl(1 + \frac 1n\bigr)^n$ |
| $10$ | $2.5937$ |
| $100$ | $2.7048$ |
| $1000$ | $2.7169$ |
| $10{,}000$ | $2.7181$ |
| $\downarrow$ | $\downarrow$ |
| $\infty$ | $\text{e}$ |
We can get these #s [the numbers in the second column] AS CLOSE TO $\,\text{e}\,$ as desired, by making $\,n\,$ sufficiently large!
[graph] labeled $\,y = \text{e}^x\,,$ “THE” exponential fct [function]
SPECIAL PROPERTY of the NATURAL EXPONENTIAL FCT [function]
[graph] shows point $\,(x,\text{e}^x)\,$ on graph of $\,y = \text{e}^x\,,$ slope of tangent line $\,= \text{e}^x\,,$ $y$-value of point tells the slope of the tangent line!
Imagine walking along a curve, from left to right. AT EACH INSTANT, the slope of the tangent line tells how you're rising/falling.
[graph] shows a point on the graph of $\,y = \text{e}^x\,$ with $y$-value equal to $\,100\,$; at this point, the $y$-values are changing $\,100\,$ times faster than the $x$-values!
| If $\,x\,$ changes by: | we expect $\,y\,$ to change by about: |
| $1$ | $100$ |
| $0.1$ | $0.1(100) = 10$ |
| $-0.01$ | $-0.01(100) = -1$ |
| $\Delta x$ | $100\Delta x$ |

NOTE:
$$ \begin{gather} \text{SIMPLE INTEREST}\cr = (\text{PRINCIPAL})(\text{RATE})(\text{TIME}) \end{gather} $$COMPOUND INTEREST
... involves ADDING IN INTEREST at regular intervals.
Let:
- $P = \,$ initial investment
- $r = \,$ annual interest rate ($\,2\% = 0.02\,$)
-
$n = \,$ # [number] of times, per year, that interest
is added in
$\hphantom{n} = \,$ # of COMPOUNDING PERIODS per yearNOTE:
$$ n\ \frac{\text{cmping per}}{\text{yr}} = \frac{1 \text{ cmping per}}{\frac 1n \text{ yrs}} $$ [cmping per = compounding period] - $t = \,$ # yrs [years]
- $A = \,$ AMT [amount] after $\,t\,$ yrs
| After: | [Principal + Interest:] |
| $\color{red}{1}\,$ cmpding [compounding] period: | $$ \begin{align} &P + P(r)(\frac 1n)\cr &\quad = \color{red}{P(1 + \frac rn)^1} \end{align} $$ |
| $\color{red}{2}\,$ [cmpding periods]: | $$ \begin{align} &P(1 + \frac rn)\cr &\quad + P(1+\frac rn)(r)(\frac 1n)\cr &\quad = \color{red}{P(1+\frac rn)^2} \end{align} $$ |
| $\vdots$ | $\vdots$ |
| $\color{red}{n}\,$ ($\,1\,$ yr) | $\color{red}{P(1+\frac rn)^n}$ |
| $\vdots$ | $\vdots$ |
| $\color{red}{2n}\,$ ($\,2\,$ yrs) | $\color{red}{P(1+\frac rn)^{n\cdot 2}}$ |
| $$ A = P(1 + \frac rn)^{nt} $$ | |
CONTINUOUS COMPOUNDING
$$ \begin{gather} {\small\text{What happens as we}}\cr \underbrace{\small\text{add in interest more & more frequently?}}_{\text{let } n\rightarrow\infty} \end{gather} $$Let $\,\frac 1m = \frac rn\,,$ so $\,n = mr\,.$
$$ \begin{align} &P(1+\frac rn)^{nt} \cr &\quad = P(1 + \frac 1m)^{mrt}\cr &\quad = P\left[(1+\frac 1m)^m\right]^{rt}\cr &\quad \rightarrow P{\text{e}}^{rt} \end{align} $$| $$A = P{\text{e}}^{rt}$$ |
| CONTINUOUS COMPOUNDING: interest is added in at the INSTANT it's earned! |

Exponential Growth
... is modeled by:
$$ \underbrace{n(t)}_{\text{# at time $\,t$}} = \underbrace{n_0}_{\substack{\text{# at}\cr \text{time $\,0\,,$}\cr n(0)}}\,{\text{e}}^{rt} $$($\,r = \,$ relative rate of growth)
Key idea, from Calculus: [graph shows point $\,(t,n_o{\text{e}}^{rt})\,$ with tangent line at this point; slope of tangent line is $\,r\cdot n_0{\text{e}}^{rt}\,$]
How fast is population increasing at time $\,t\,$?
ANSWER: $\,r\,$ times as fast as current population!!
The growth rate is proportional to the current size!
A Typical EXP [exponential] Growth Problem
The pop [population] of a city was $\,680{,}000\,$ in $\,1992\,$; relative growth rate is $\,12\%/\text{yr}\,.$ What is the population $\,t\,$ years after $\,1992\,$? In $\,2000\,$?
First Solution: Let $\,t = 0\,$ in $\,1992\,$; measure $\,n(t)\,$ in THOUSANDS (i.e., $\,680\,$ means $\,680\,$ THOUSAND).
$$ n(t) = 680{\text{e}}^{0.12t} $$The year $\,2000\,$ corresponds to $\,t = 8\,$:
$$ \begin{align} n(8) &= 680{\text{e}}^{0.12(8)}\cr &\approx 1775{.}954 \end{align} $$In $\,2000\,,$ the pop [population] will be about $\,1{,}775{,}954\,$ people.
Alternative solution:
$$ n(t) = 680{,}000{\text{e}}^{0.12t} $$ $$ \begin{align} n(8) &= 680{,}000{\text{e}}^{0.12t}\cr &\approx 1{,}775{,}954 \end{align} $$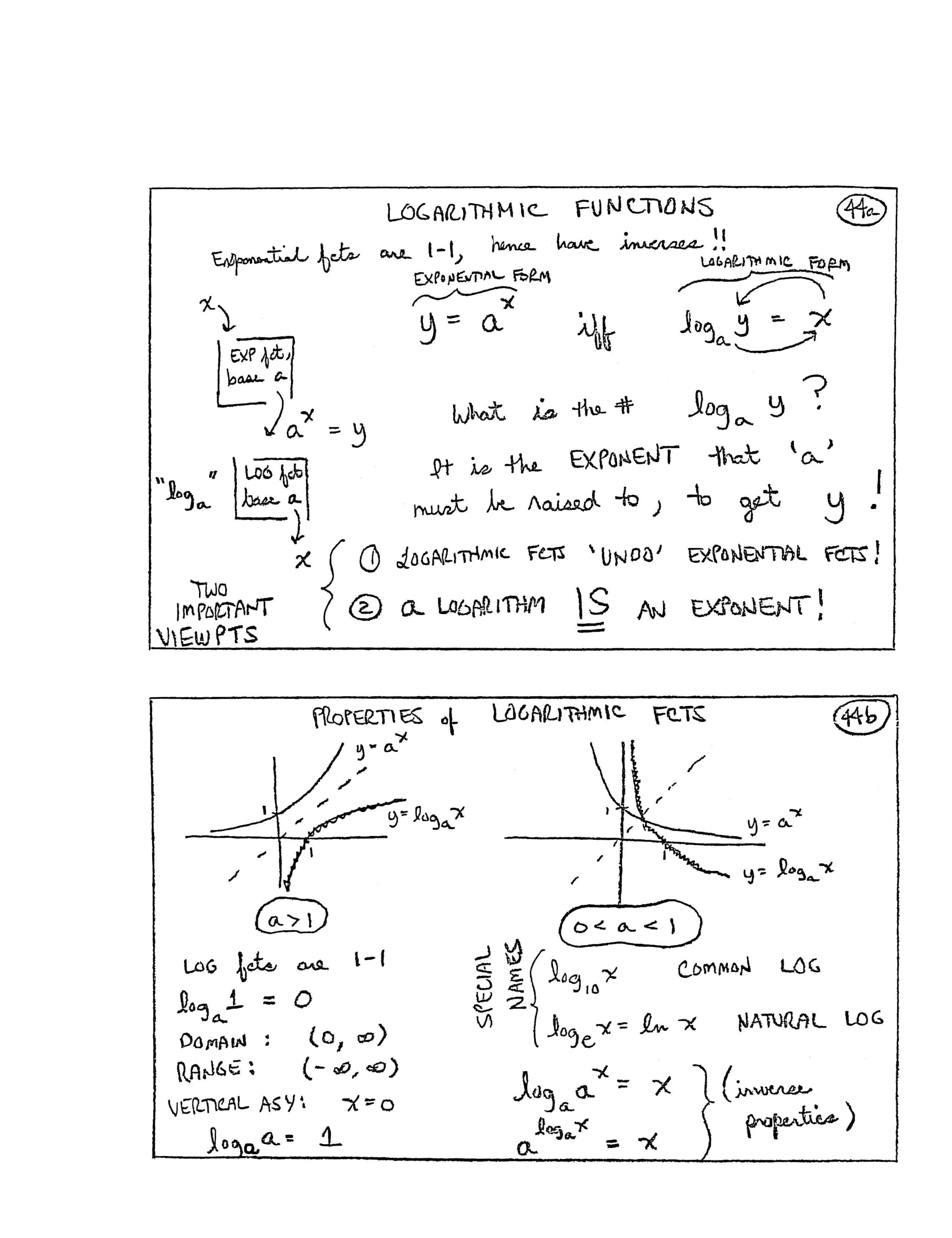
Logarithmic Functions: Review and Additional Properties (Part 2)
LOGARITHMIC FUNCTIONS
Exponential fcts [functions] are $\,1{-}1\,$ [one-to-one], hence have inverses!!
$$ \overbrace{y = {\text{a}}^x}^{\text{exponential form}} \ \text{iff}\ \overbrace{\log_a y = x}^{\text{logarithmic form}} $$[Note: ‘iff’ means ‘if and only if’. On the logarithmic form, arrow starts with $\,a\,,$ moves to $\,x\,,$ then to $\,y\,,$ giving $\,a^x = y\,.$]
[Sketch shows $\,x\,$ being dropped into the ‘EXP fct [exponential function], base $\,a\,$’ box, with $\,a^x = y\,$ as the output. Then, $\,y\,$ is dropped into the ‘$\,\text{log}_a\,$’ box, ‘LOG fct [logarithmic function], base $\,a\,$’ giving the output $\,x\,.$]
What is the # [number] $\,\text{log}_a y\,$?
It is the EXPONENT that ‘$\,a\,$’ must be raised to, to get $\,y\,$!
TWO IMPORTANT VIEWPTS [viewpoints]
- Logarithmic fcts [functions] ‘UNDO’ exponential fcts!
- A logarithm IS an exponent!
PROPERTIES of LOGARITHMIC FCTS [functions]
[first graph, $\,a\gt 1\,,$ showing the graph of $\,y = a^x\,$ and its inverse $\,y = \text{log}_a x\,,$ mirrored about the line $\,y = x\,.$]
[second graph, $\,0\lt a\lt 1\,,$ showing the graph of $\,y = a^x\,$ and its inverse $\,y = \text{log}_a x\,,$ mirrored about the line $\,y = x\,.$]
- LOG fcts [logarithmic functions] are $\,1{-}1\,$ [one-to-one]
- $\text{log}_a 1 = 0$
- DOMAIN: $\,(0,\infty)$
- RANGE: $\,(-\infty,\infty)$
- VERTICAL ASY [asymptote]: $\,x = 0$
- $\text{log}_a a = 1$
-
SPECIAL NAMES:
$\text{log}_{10}x\,$ COMMON LOG
$\text{log}_e x = \ln x\,$ NATURAL LOG -
INVERSE PROPERTIES:
$\text{log}_a a^x = x$
$a^{\text{log}_a x} = x$

LAWS of LOGARITHMS
Let $\,a\gt 0\,,$ $\,a\ne 1\,,$ $\,A\gt 0\,,$ $\,B\gt 0\,,$ $\,c\in\Bbb R\,.$ Then,
$$ \log_a(AB) = \log_a A + \log_a B $$(the log of a PRODUCT is the SUM of the logs)
$$ \log_a(\frac AB) = \log_a A - \log_a B $$(the log of a QUOTIENT is the DIFFERENCE of the logs)
$$ \log_a(A^c) = c\,\log_a A $$(You can bring exponents down front)
Sample Proof
Spse [suppose] $\,\log_a A = u\,$ and $\,\log_a B = v\,,$ so $\,a^u = A\,$ and $\,a^v = B\,.$ Then,
$$ \begin{align} \log_a AB &= \log_a a^u a^v\ \text{(substitution)}\cr &= \log_a a^{u+v}\ \text{(law of exponents)}\cr &= u + v\ \text{(inverse property)}\cr &= \log_a A + \log_a B\ \text{(subst [substitution])} \end{align} $$
CHANGE of BASE FORMULA
Let $\,a\,$ and $\,b\,$ be positive real #s [numbers] that are not equal to $\,1\,,$ and let $\,x \gt 0\,.$ Then:
$$ \log_b x = \frac{\log_a x}{\log_a b} $$You can switch from any base to any other base—the price you pay: you must $\,\div\,$ [divide] by the log, to the new base, of the old base.
Consequence: any log curve is just a VERTICAL SCALING of any other log curve!
DERIVATION
The following equations are EQUIVALENT:
$$ \begin{gather} y = \log_b x\cr \text{(LHS [left-hand-side]}\cr \text{of Change-of-base formula)}\cr\cr b^y = x\cr \text{(equiv [equivalent]}\cr \text{EXP [exponential] form)}\cr\cr \log_a b^y = \log_a x\cr \text{(log fcts are 1-1)}\cr\cr y \log_a b = \log_a x\cr \text{(property of logs)}\cr\cr y = \frac{\log_a x}{\log_a b}\cr \text{(divide by $\,\log_a b\,$)} \end{gather} $$
SOLVING EXPONENTIAL EQUATIONS
(an exponential equation has at least one VARIABLE in an EXPONENT)
- ISOLATE an exponential expression (i.e., get something of the form $\,a^{(\text{stuff})}\,$ all by itself on one side of equation)
- ‘UNDO’ the exponential fct [function] with a log! (usually use $\,\log\,$ or $\,\ln\,$)
- SOLVE for the variable
- CHECK in original equation
EXAMPLES
SOLVE:
$$ \begin{gather} 8 \cdot 5^{2x-1} = 20\cr\cr 5^{2x-1} = \frac{20}{8} = \frac{5}{2}\cr\cr \ln 5^{2x-1} = \ln \frac{5}{2}\cr\cr (2x-1) \ln 5 = \ln 2.5\cr\cr 2x \ln 5 - \ln 5 = \ln 2.5\cr\cr 2x \ln 5 = \ln 2.5 + \ln 5\cr\cr x = \frac{\ln 2.5 + \ln 5}{2 \ln 5} \end{gather} $$(NO APPROXIMATION until final step!)
SOLVE:
$$\text{e}^{2x} - \text{e}^{x} - 6 = 0$$(‘fake’ quadratic!)
$$(\text{e}^x)^2 - (\text{e}^x) - 6 = 0$$Let $\,u =\text{e}^x\,$:
$$ \begin{gather} u^2 - u - 6 = 0\cr\cr (u-3)(u+2) = 0\cr\cr (\text{e}^x-3)(\text{e}^x+2) = 0\cr\cr \text{e}^x = 3 \quad \text{or} \quad \overbrace{\text{e}^x = -2}^{\text{exp fcts can't be negative}}\cr\cr x = \ln 3 \end{gather} $$[Don't forget to check your solutions in the original equations!]

SOLVING LOGARITHMIC EQUATIONS
(a logarithmic equation has @ [at] least one variable INSIDE a logarithm)
- ISOLATE a logarithm (may need to combine several logs using properties of logs; get $\,\log_a(\text{STUFF})\,$ all by itself)
- ‘UNDO’ the log with a (corresponding) exponential fct [function]. (OR ... write down the EQUIVALENT exponential equation)
- SOLVE for the variable.
- CHECK in original equation. DISCARD any extraneous solution(s).
EXAMPLES
SOLVE:
$$ \begin{gather} 4 + 3 \log(2x) = 16\cr\cr 3 \log(2x) = 12\cr\cr \log(2x) = 4\cr\cr 10^4 = 2x\cr\cr x = \frac{10^4}{2} = 5000 \end{gather} $$SOLVE:
$$ \begin{gather} \log(x + 2) + \log(x - 1) = 1\cr\cr \log(x + 2)(x - 1) = 1\ \ \bigstar\cr\cr 10^1 = (x + 2)(x - 1)\cr\cr x^2 + x - 2 = 10\cr\cr x^2 + x - 12 = 0\cr\cr (x + 4)(x - 3) = 0\cr\cr \xcancel{x = -4}\ \ \text{or}\ \ \underset{\checkmark}{x = 3} \end{gather} $$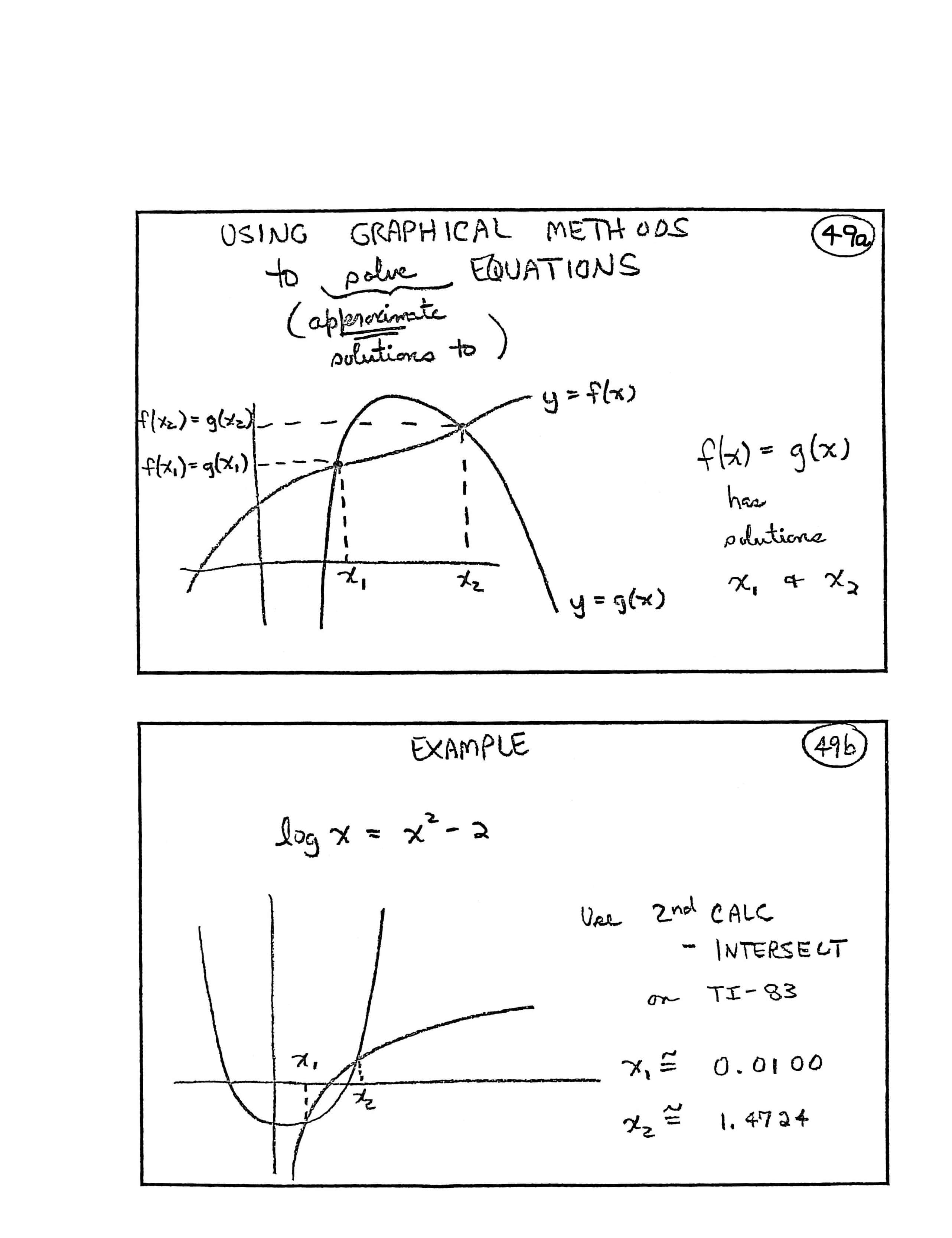
USING GRAPHICAL METHODS to solve (approximate solutions to) EQUATIONS
[graph] Graph shows curves $\,y = f(x)\,$ and $\,y = g(x)\,$ with intersection points $\,(x_1,\underbrace{f(x_1)}_{=\, g(x_1)})\,$ and $\,(x_2,\underbrace{f(x_2)}_{=\, g(x_2)})\,$
$f(x) = g(x)\,$ has solutions $\,x_1\,$ and $\,x_2\,$
EXAMPLE
[Solve:]
$$ \log x = x^2 - 2 $$[graph] Graph shows $\,y = \log x\,$ and $\,y = x^2 - 2\,$ with intersection points at $\,x_1\,$ and $\,x_2\,$
Use $2$nd CALC – INTERSECT on TI-83 $$ \begin{gather} x_1 \approx 0.0100\cr\cr x_2 \approx 1.4724 \end{gather} $$

DOUBLING TIME for exponential growth fcts [functions]
[graph] Labeled $\,A(t) = A_0{\text{e}}^{rt}\,,$ $\,r\gt 0\,.$ Points on graph: $\,\bigl(t,A(t)\bigr)\,$ and $\,\bigl(t+\Delta t\,,\,\underbrace{A(t+\Delta t)}_{= 2A(t)}\bigr)\,.$ Note that the distance between $\,t\,$ and $\,t + \Delta t\,$ is $\,\Delta t\,,$ which asks the question: How long?
The DOUBLING TIME depends only on the growth rate, $\,r\,$ (does NOT depend on $\,t\,$):
Find $\,\Delta t\,$ for which $\,A(t + \Delta t) = 2A(t)\,$:
$$ \begin{gather} \cancel{A_0} \text{e}^{r(t + \Delta t)} = 2(\cancel{A_0} \text{e}^{rt})\cr\cr \cancel{\text{e}^{rt}} \text{e}^{r \Delta t} = 2 \cancel{\text{e}^{rt}}\cr\cr \ln(\text{e}^{r \Delta t}) = \ln 2\cr\cr r \Delta t = \ln 2\cr\cr \Delta t = \dfrac{\ln 2}{r} \end{gather} $$HALF-LIFE for exponential decay fcts [functions]
(Half-life is the amt [amount] of time it takes for quantity to be cut in half)
[graph] Labeled $\,A(t) = A_0{\text{e}}^{-rt}\,,$ $\,r\gt 0\,.$ Points on graph: $\,\bigl(t,A(t)\bigr)\,$ and $\,\bigl(t+\Delta t\,,\,\underbrace{A(t+\Delta t)}_{= \frac 12A(t)}\bigr)\,.$ Note that the distance between $\,t\,$ and $\,t + \Delta t\,$ is $\,\Delta t\,.$
The half-life depends only on the decay rate, $\,r\,$:
Find $\,\Delta t\,$ for which $\,A(t + \Delta t) = \frac{1}{2} A(t)\,$:
$$ \begin{gather} \cancel{A_0} \text{e}^{-r(t + \Delta t)} = \frac{1}{2} \cancel{A_0} \text{e}^{-rt}\cr\cr \cancel{\text{e}^{-rt}} \text{e}^{-r \Delta t} = \frac{1}{2} \cancel{\text{e}^{-rt}}\cr\cr \text{e}^{-r \Delta t} = 2^{-1}\cr\cr -r \Delta t = \ln 2^{-1}\cr\cr \Delta t = \dfrac{-\ln 2}{-r} = \dfrac{\ln 2}{r} \end{gather} $$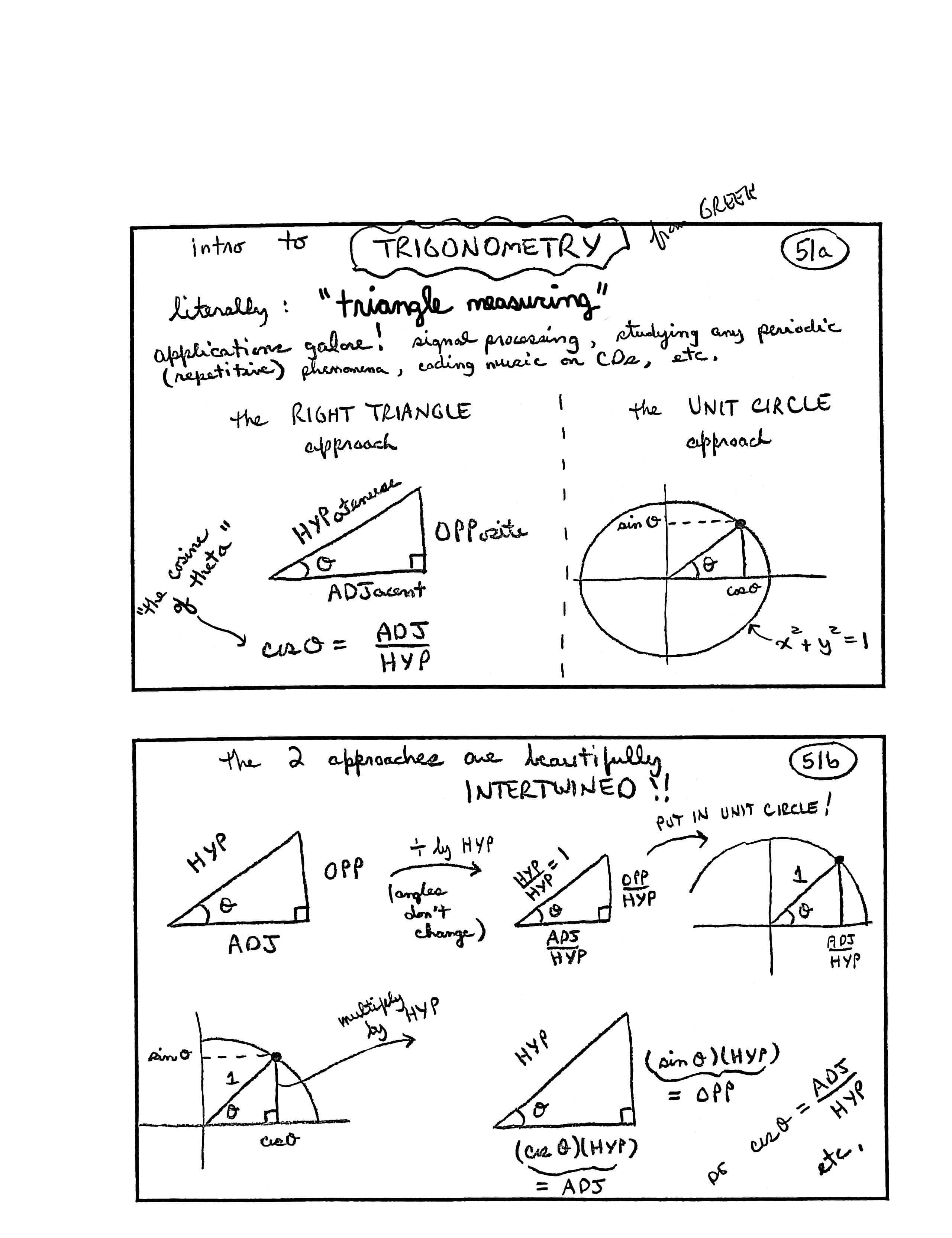
The Right Triangle Approach to Trigonometry
The Unit Circle Approach to Trigonometry
Compatibility of the Right Triangle and Unit Circle Approaches
INTRO TO TRIGONOMETRY
(from Greek: ‘trigonometry’ means, literally, ‘triangle measuring’)
Applications galore! Signal processing, studying any periodic (repetitive) phenomena, coding music on CDs, etc.
The RIGHT TRIANGLE approach:
[diagram: right triangle with acute angle $\,\theta\,,$ ADJacent side, OPPosite side, HYPotenuse]
$$ \overbrace{\cos\theta}^{\text{the cosine of theta}} = \frac{\text{ADJ}}{\text{HYP}}$$The UNIT CIRCLE approach:
[diagram: circle (equation $\,x^2 + y^2 = 1\,$) with radius $\,1\,$ and angle $\,\theta\,,$ point on circle with $x$-value equal to $\,\cos\theta\,$ and $y$-value equal to $\,\sin\theta$ ]
The 2 approaches are beautifully INTERTWINED!!
[diagram: right triangle with acute angle $\,\theta\,$ and sides ADJ, OPP, HYP] $\,\longrightarrow\,$ $\,\div\,$ (divide) by HYP (angles don't change) [diagram: right triangle with acute angle $\,\theta\,,$ and sides $\,\frac{\text{ADJ}}{\text{HYP}}\,,$ $\,\frac{\text{OPP}}{\text{HYP}}\,,$ and $\,\frac{\text{HYP}}{\text{HYP}} = 1\,$] $\,\longrightarrow\,$ Put in unit circle! [diagram with unit circle, angle $\,\theta\,,$ point on circle with $x$-value equal to $\,\frac{\text{ADJ}}{\text{HYP}}\,$ ]
[diagram: unit circle with acute angle $\,\theta\,,$ point with $x$-value equal to $\,\cos\theta\,$ and $y$-value equal to $\,\sin\theta\,$] $\,\longrightarrow\,$ multiply by HYP [diagram: right triangle with angle $\,\theta\,,$ sides $\,\underbrace{(\cos\theta)(\text{HYP})}_{= \text{ADJ}}\,$ and $\,\underbrace{(\sin\theta)(\text{HYP})}_{= \text{OPP}}\,$] so $\,\cos\theta = \frac{\text{ADJ}}{\text{HYP}}\,,$ etc.
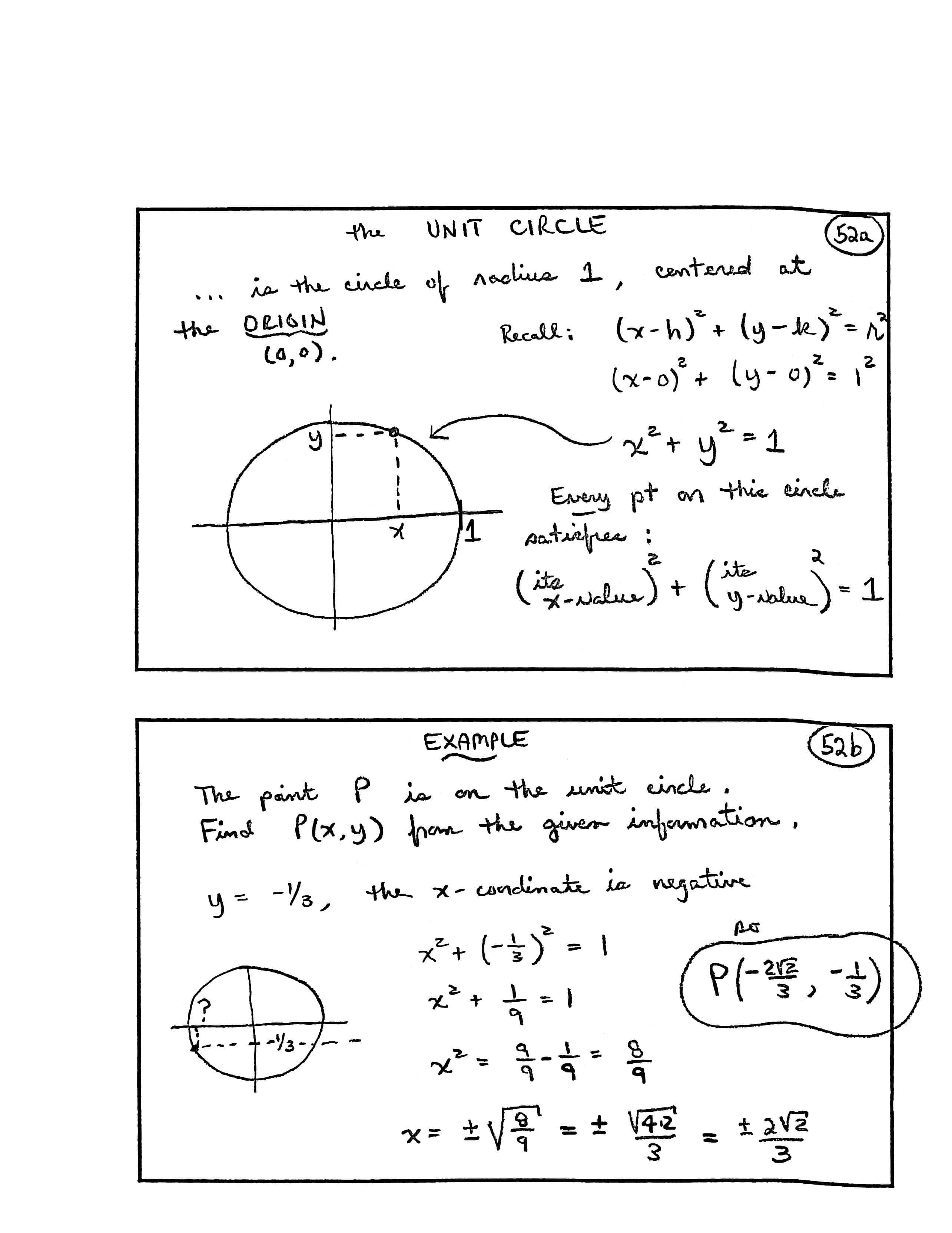
the UNIT CIRCLE
... is the circle of radius $\,1\,,$ centered at the ORIGIN $\,(0, 0)\,.$
Recall:
$$ \begin{gather} (x - h)^2 + (y - k)^2 = r^2\cr\cr (x - 0)^2 + (y - 0)^2 = 1^2\cr\cr x^2 + y^2 = 1 \end{gather} $$[sketch: circle with radius $\,1\,,$ point $\,(x,y)\,$ on circle]
Every point on this circle satisfies:
$$ \text{(its $x$-value)}^2 + \text{(its $y$-value)}^2 = 1 $$EXAMPLE
The point $\,P\,$ is on the unit circle. Find $\,P(x, y)\,$ from the given information: $\,y = -\frac{1}{3}\,,$ the $x$-coordinate is negative
[sketch: unit circle, showing the two points on the circle with $\,y = -\frac 13\,$; we want the point with the negative $x$-value]
$$ \begin{gather} x^2 + (-\frac{1}{3})^2 = 1\cr\cr x^2 + \frac{1}{9} = 1\cr\cr x^2 = \frac{9}{9} - \frac{1}{9} = \frac{8}{9}\cr\cr x = \pm \sqrt{\frac{8}{9}} = \pm \frac{\sqrt{4 \cdot 2}}{3} = \pm \frac{2\sqrt{2}}{3} \end{gather} $$So:
$$ P = \left(-\frac{2\sqrt{2}}{3}\,,\,-\frac{1}{3}\right) $$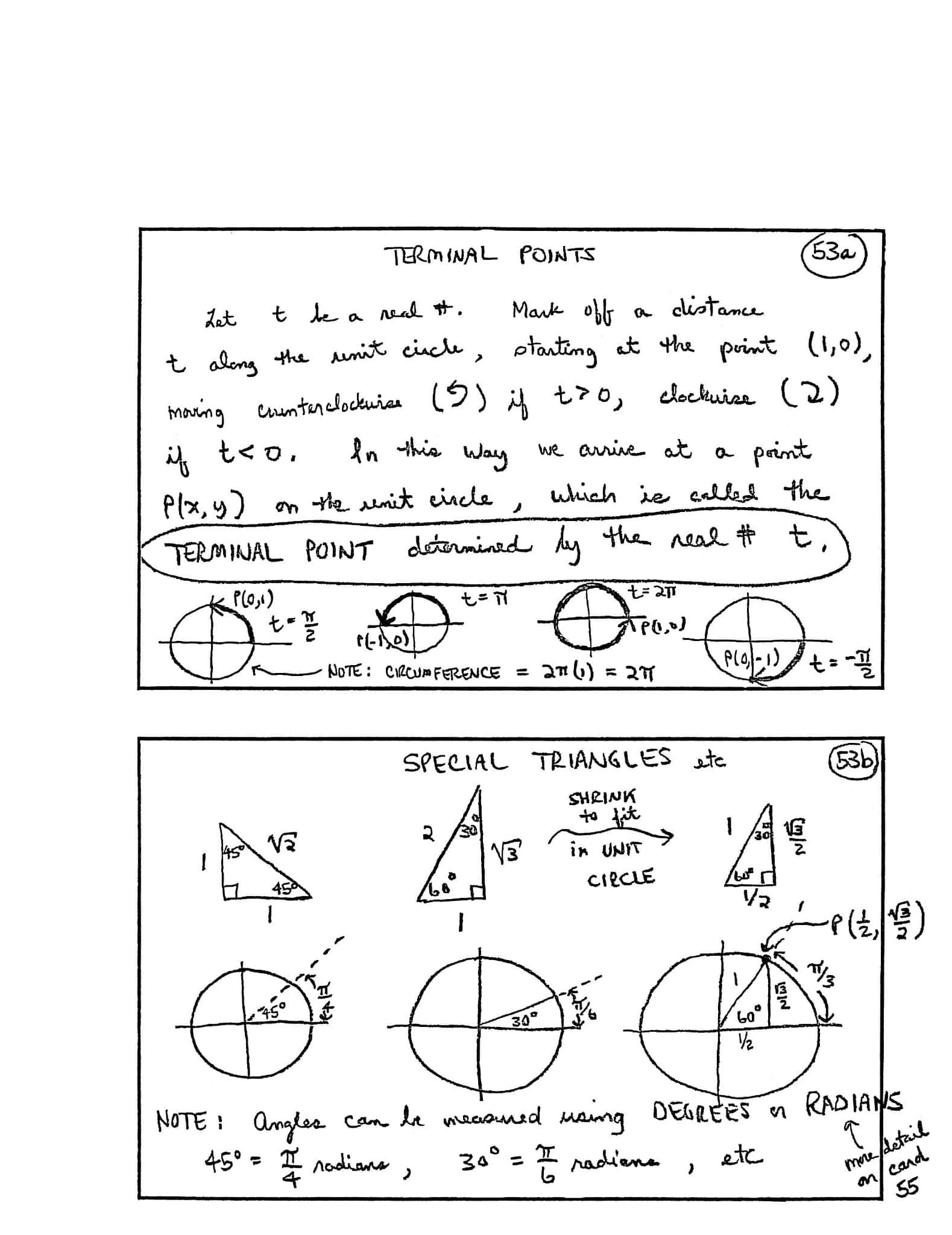
TERMINAL POINTS
Let $\,t\,$ be a real number.
Mark off a distance $\,t\,$ along the unit circle, starting at the point $\,(1, 0)\,,$ moving counterclockwise (↺) if $\,t \gt 0\,,$ clockwise (↻) if $\,t \lt 0\,.$
In this way, we arrive at a point $\,P(x, y)\,$ on the unit circle, which is called the TERMINAL POINT determined by the real number $\,t\,.$
[Examples (unit circle diagrams)]
-
[Unit circle, start at point $\,(1,0)\,,$ travel counterclockwise distance $\,t = \frac\pi 2\,,$ ending at $\,P(0,1)\,$]
Note: CIRCUMFERENCE $\,= 2\pi(1) = 2\pi$
- [Unit circle, start at point $\,(1,0)\,,$ travel counterclockwise distance $\,t = \pi\,,$ ending at $\,P(-1,0)\,$]
- [Unit circle, start at point $\,(1,0)\,,$ travel counterclockwise distance $\,t = 2\pi\,,$ ending at $\,P(1,0)\,$]
- [Unit circle, start at point $\,(1,0)\,,$ travel clockwise distance $\,\frac\pi 2\,$ ($\,t = -\frac\pi 2\,$), ending at $\,P(0,-1)\,$]
SPECIAL TRIANGLES, etc.
[Note: Triangles are ‘shrunk’ to fit into unit circle, by dividing all sides by the length of the hypotenuse.]
[First column: $\,45^\circ{-}45^\circ{-}90^\circ\,$ triangle; sides $\,1\,,$ $\,1\,,$ $\,\sqrt 2\,$; shrink to fit in unit circle, subtending arc length $\,\frac\pi 4\,$]
[Middle column: $\,30^\circ{-}60^\circ{-}90^\circ\,$ triangle; sides $\,1\,,$ $\,\sqrt 3\,,$ $\,2\,$; shrink to fit in unit circle ($\,30^\circ\,$ angle at center); subtending arc length $\,\frac\pi 6\,$]
[Last column: $\,30^\circ{-}60^\circ{-}90^\circ\,$ triangle; sides $\,\frac12\,,$ $\,\frac{\sqrt 3}2\,,$ $\,1\,$; already shrunk to fit in unit circle ($\,60^\circ\,$ angle at center); subtending arc length $\,\frac\pi 3\,$ with terminal point $\,P(\frac 12,\frac{\sqrt 3}2)\,$]
Note: Angles can be measured using DEGREES or RADIANS (more detail [on radians] on card 55):
$$ \begin{gather} 45^\circ = \frac{\pi}{4}\ \text{radians}\cr\cr 30^\circ = \dfrac{\pi}{6}\ \text{radians}\cr \text{etc} \end{gather} $$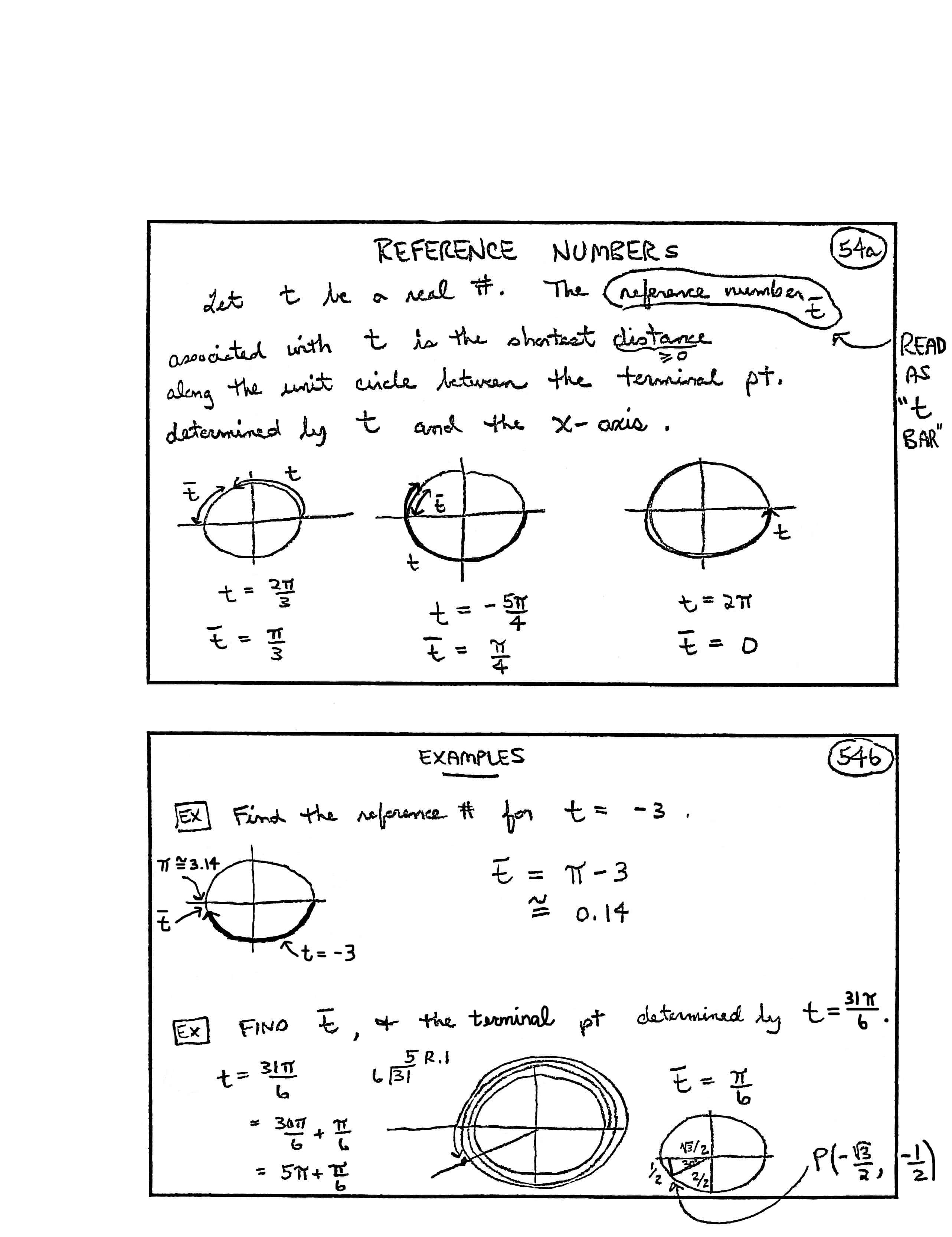
REFERENCE NUMBERS
Let $\,t\,$ be a real number.
The reference number $\,\bar{t}\,$ (read as as ‘$\,t\,$ bar’) associated with $\,t\,$ is the shortest distance (along the unit circle) between the terminal point determined by $\,t\,$ and the $x$-axis. (Note: distance is always $\,\ge 0\,.$)
[first sketch] Lay off $\,t = \frac{2\pi}3\,$; $\,\bar{t} = \frac\pi 3$
[second sketch] Lay off $\,t = -\frac{5\pi}4\,$; $\,\bar{t} = \frac\pi 4$
[third sketch] Lay off $\,t = 2\pi\,$; $\,\bar{t} = 0$
EXAMPLES
[first example] Find the reference number for $\,t = -3\,.$
[Sketch: Since $\,t \lt 0\,,$ it is laid off in the clockwise direction. Half the circle has length $\,\pi\approx 3.14\,,$ so this is just a bit less than half of the circle.]
$$ \begin{align} \bar{t} &= \pi - 3\cr &\approx 0.14 \end{align} $$[second example] Find $\,\bar{t}\,,$ and the terminal point determined by $\,t = \frac{31\pi}6\,.$
[Note: $6\,$ goes into $\,31\,$ five times, with a remainder of $\,1\,.$]
$$ \begin{align} t &= \frac{31\pi}6\cr\cr &= \frac{30\pi}6 + \frac\pi 6\cr\cr &= 5\pi + \frac\pi 6 \end{align} $$[Sketch: Lay off $\,5\pi\,$ (five half-circles) in the counterclockwise direction, then an extra $\,\frac\pi 6\,.$]
$$\bar{t} = \frac\pi 6$$[Sketch: Recognize that $\,\frac\pi 6 = 30^\circ\,.$ Draw in the $\,30^\circ{-}60^\circ{-}90^\circ\,$ triangle, with sides labeled and ‘shrunk’ so that the hypotenuse is $\,1\,.$ Then, we can read off the coordinates of the terminal point:]
$$ P\bigl(-\frac{\sqrt{3}}{2}\,,\, -\frac{1}{2}\bigr) $$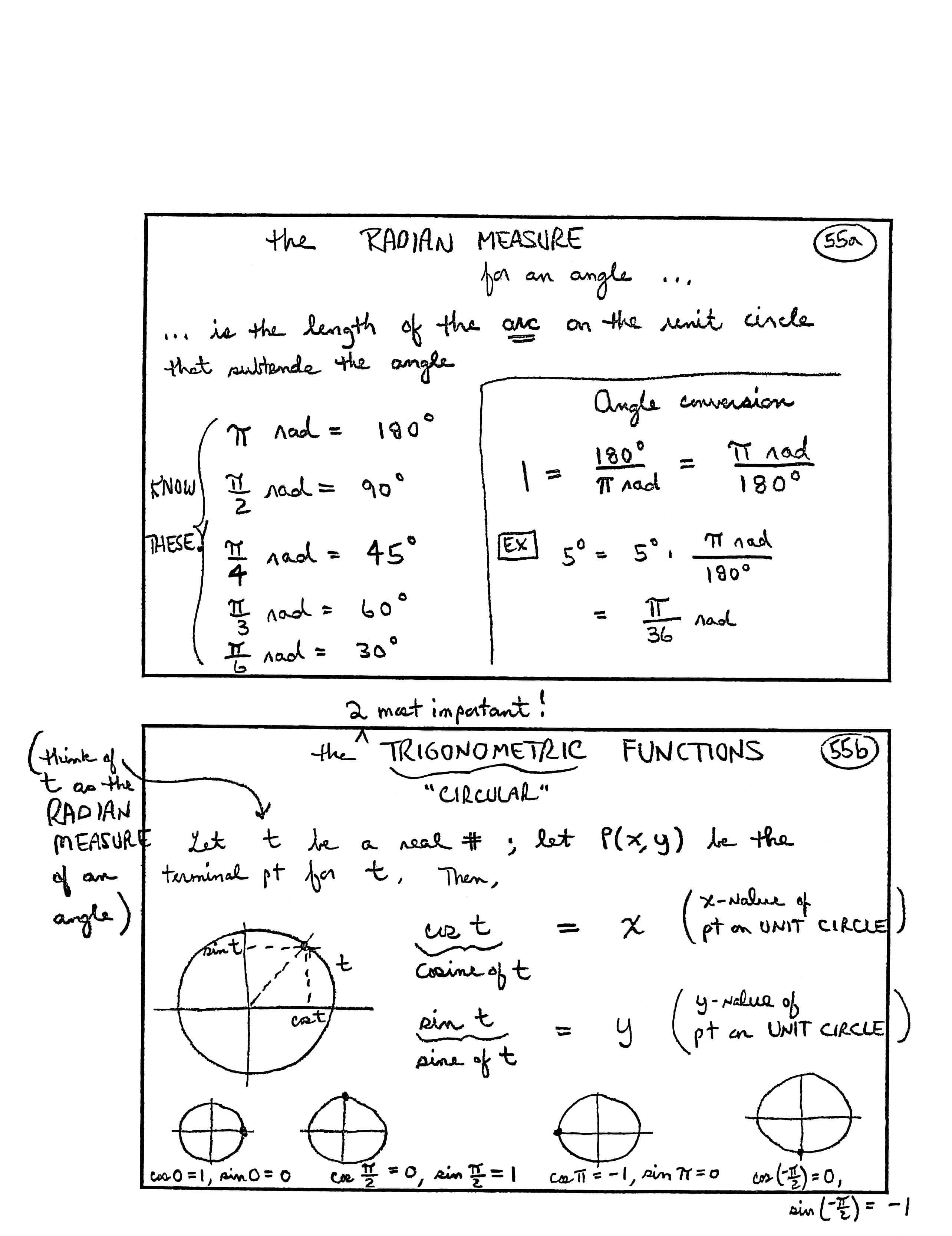
the RADIAN MEASURE (for an angle ...)
... is the length of the arc on the unit circle that subtends the angle.
KNOW THESE!
$$ \begin{gather} \pi \text{ rad} = 180^\circ\cr\cr \frac{\pi}{2} \text{ rad} = 90^\circ\cr\cr \frac{\pi}{4} \text{ rad} = 45^\circ\cr\cr \frac{\pi}{3} \text{ rad} = 60^\circ\cr\cr \frac{\pi}{6} \text{ rad} = 30^\circ \end{gather} $$Angle conversion:
$$ 1 = \frac{180^\circ}{\pi\ \text{rad}} = \frac{\pi\ \text{rad}}{180^\circ} $$EX [Example]:
$$ \begin{align} 5^\circ &= 5^\circ \cdot \frac{\pi\ \text{rad}}{180^\circ}\cr\cr &= \frac{\pi}{36}\ \text{rad} \end{align} $$the (2 most important!) TRIGONOMETRIC (“CIRCULAR”) FUNCTIONS
Let $\,t\,$ be a real number; let $\,P(\color{red}{x}, \color{blue}{y})\,$ be the terminal point for $\,t\,.$ (Think of $\,t\,$ as the RADIAN MEASURE of an angle.) Then:
[sketch: unit circle with angle $\,t\,$ laid off; the terminal point has $x$-value $\,\cos t\,$ and $y$-value $\,\sin t\,$
$$ \begin{gather} \underbrace{\cos t}_{\text{cosine of } t} = \color{red}{x}\cr \text{($x$-value of pt [point] on unit circle)}\cr\cr \underbrace{\sin t}_{\text{sine of } t} = \color{blue}{y}\cr \text{($y$-value of pt on unit circle)} \end{gather} $$[Examples (from unit circle visualization):]
[unit circle showing point $\,(1,0)\,$] $$ \begin{gather} \cos 0 = 1\cr \sin 0 = 0 \end{gather} $$
[unit circle showing point $\,(0,1)\,$] $$ \begin{gather} \cos \frac\pi 2 = 0\cr \sin \frac\pi 2 = 1 \end{gather} $$
[unit circle showing point $\,(-1,0)\,$] $$ \begin{gather} \cos \pi = -1\cr \sin \pi = 0 \end{gather} $$
[unit circle showing point $\,(0,-1)\,$] $$ \begin{gather} \cos (-\frac\pi 2) = 0\cr \sin (-\frac\pi 2) = -1 \end{gather} $$

the other TRIG FCTS [functions] ...
... are defined in terms of $\,\sin\,$ [sine] and $\,\cos\,$ [cosine]
$$ \begin{align} \sin t &\cr\cr \cos t &\cr\cr \tan t &= \text{‘tangent of $\,t\,$’}\cr &= \frac{\sin t}{\cos t}\cr\cr \cot t &= \text{‘cotangent of $\,t\,$’}\cr &= \frac{\cos t}{\sin t} = \frac{1}{\tan t}\cr\cr \sec t &= \text{‘secant of $\,t\,$’}\cr &= \frac{1}{\cos t}\cr\cr \csc t &= \text{‘cosecant of $\,t\,$’}\cr &= \frac{1}{\sin t} \end{align} $$[Note: reciprocals are connected: sine and cosecant; cosine and secant; tangent and cotangent]
FINDING TRIG VALUES on your calculator
Careful!! $1^\circ\,$ and $\,1\text{ rad}\,$ are VERY DIFFERENT!!
$$ 1 \text{ rad} = 1\text{ rad} \cdot \frac{180^\circ}{\pi\text{ rad}} \approx 57.3^\circ $$[circle sketch: $1\text{ rad}\approx 57^\circ\,$]
$\cos 1\,$ means cosine of $\,1\,$ radian:
$$ \cos 1 \approx 0.54 $$If you want degrees, you MUST USE THE DEGREE SIGN!!
$$ \cos 1^\circ \approx 1\ \ \text{(Why?)} $$
Use the MODE key to set RADIAN/
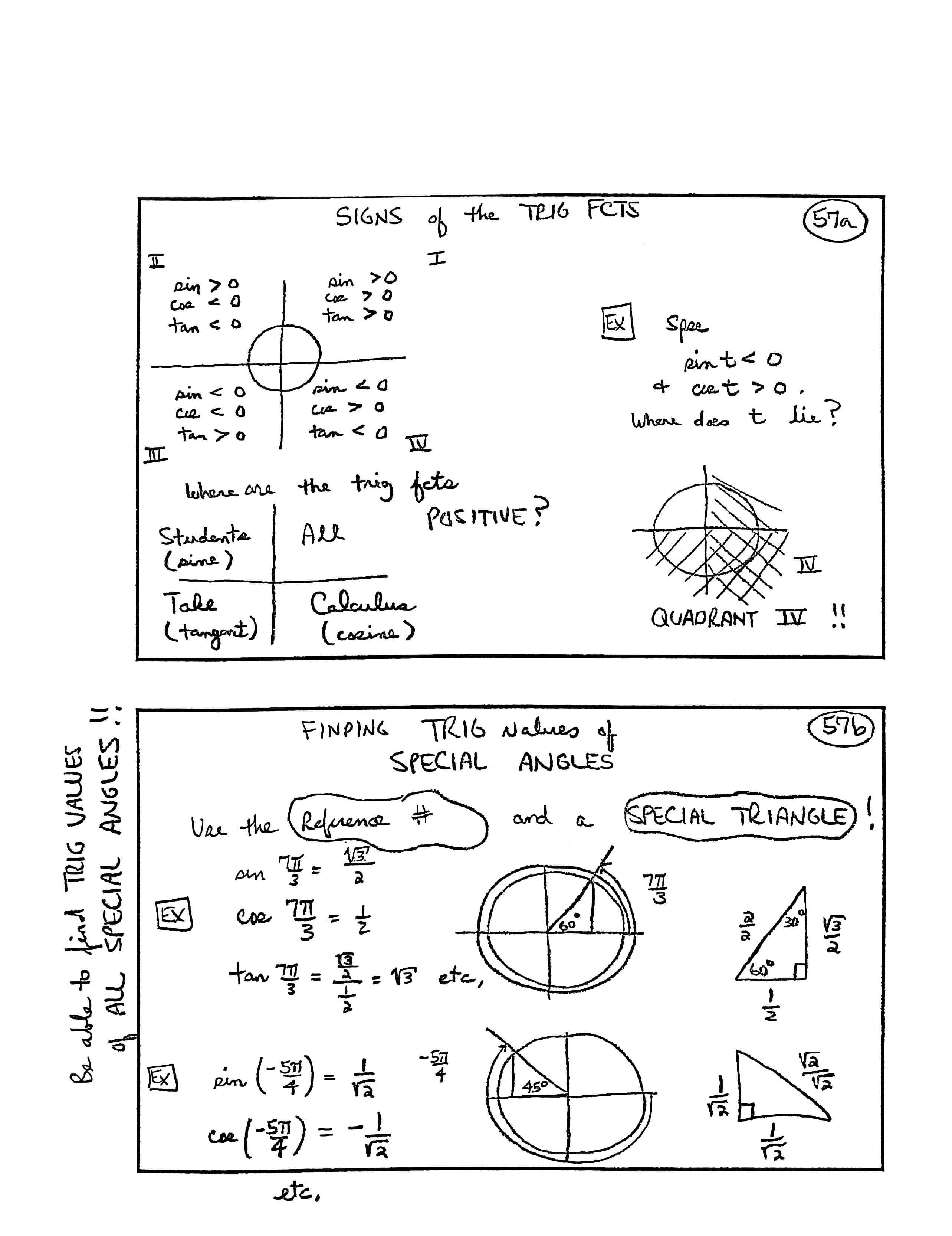
SIGNS of the TRIG FCTS [trigonometric functions]
[Unit circle divided into quadrants I–IV]
QUADRANT I:
$\sin \gt 0\,,$ $\,\cos \gt 0\,,$ $\tan \gt 0$
QUADRANT II:
$\sin \gt 0\,,$ $\,\cos \lt 0\,,$ $\,\tan \lt 0$
QUADRANT III:
$\sin \lt 0\,,$ $\,\cos \lt 0\,,$ $\,\tan \gt 0$
QUADRANT IV:
$\sin \lt 0\,,$ $\,\cos \gt 0\,,$ $\,\tan \lt 0$
Where are the trig functions POSITIVE?
[Diagram showing the phrase ‘ALL Students (sine) Take (tangent) Calculus (cosine)’]
| Quadrant | Positive Functions |
| I | ALL |
| II | sine (Students) |
| III | tangent (Take) |
| IV | cosine (Calculus) |
Example: Spse [suppose] $\,\sin t \lt 0\,$ and $\,\cos t \gt 0\,.$ Where does $\,t\,$ lie?
[Shade everything beneath the
$x$-axis;
shade everything to the right
of the
$y$-axis.
What quadrant is in
both regions?]
Answer: QUADRANT IV!!
FINDING TRIG [trigonometric] VALUES of SPECIAL ANGLES
[on side of card] Be able to find TRIG VALUES of ALL SPECIAL ANGLES!!
Use the reference # [number] and a SPECIAL TRIANGLE!
Example:
$$ \begin{align} \sin \frac{7\pi}{3} &= \frac{\sqrt{3}}{2}\cr\cr \cos \frac{7\pi}{3} &= \frac{1}{2}\cr\cr \tan \frac{7\pi}{3} &= \frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} = \sqrt{3}\,,\ \ \text{etc} \end{align} $$[unit circle showing angle $\,\frac{7\pi}3\,$ ; the reference # is $\,\frac{\pi}3 = 60^\circ\,$; special $\,30^\circ{-}60^\circ{-}90^\circ\,$ triangle, shrunk to fit in the unit circle; side lengths are $\,\frac 12\,,$ $\,\frac{\sqrt 3}2\,,$ and $\,1\,$]
Example:
$$ \begin{align} \sin \left(-\frac{5\pi}{4}\right) &= \frac{1}{\sqrt{2}}\cr\cr \cos \left(-\frac{5\pi}{4}\right) &= -\frac{1}{\sqrt{2}}\,, \ \ \text{etc} \end{align} $$[unit circle showing angle $\,-\frac{5\pi}4\,$; the reference # is $\,\frac{\pi}4 = 45^\circ\,$; special $\,45^\circ{-}45^\circ{-}90^\circ\,$ triangle, shrunk to fit in the unit circle; side lengths are $\,\frac 1{\sqrt 2}\,,$ $\,\frac1{\sqrt 2}\,,$ and $\,1\,$]
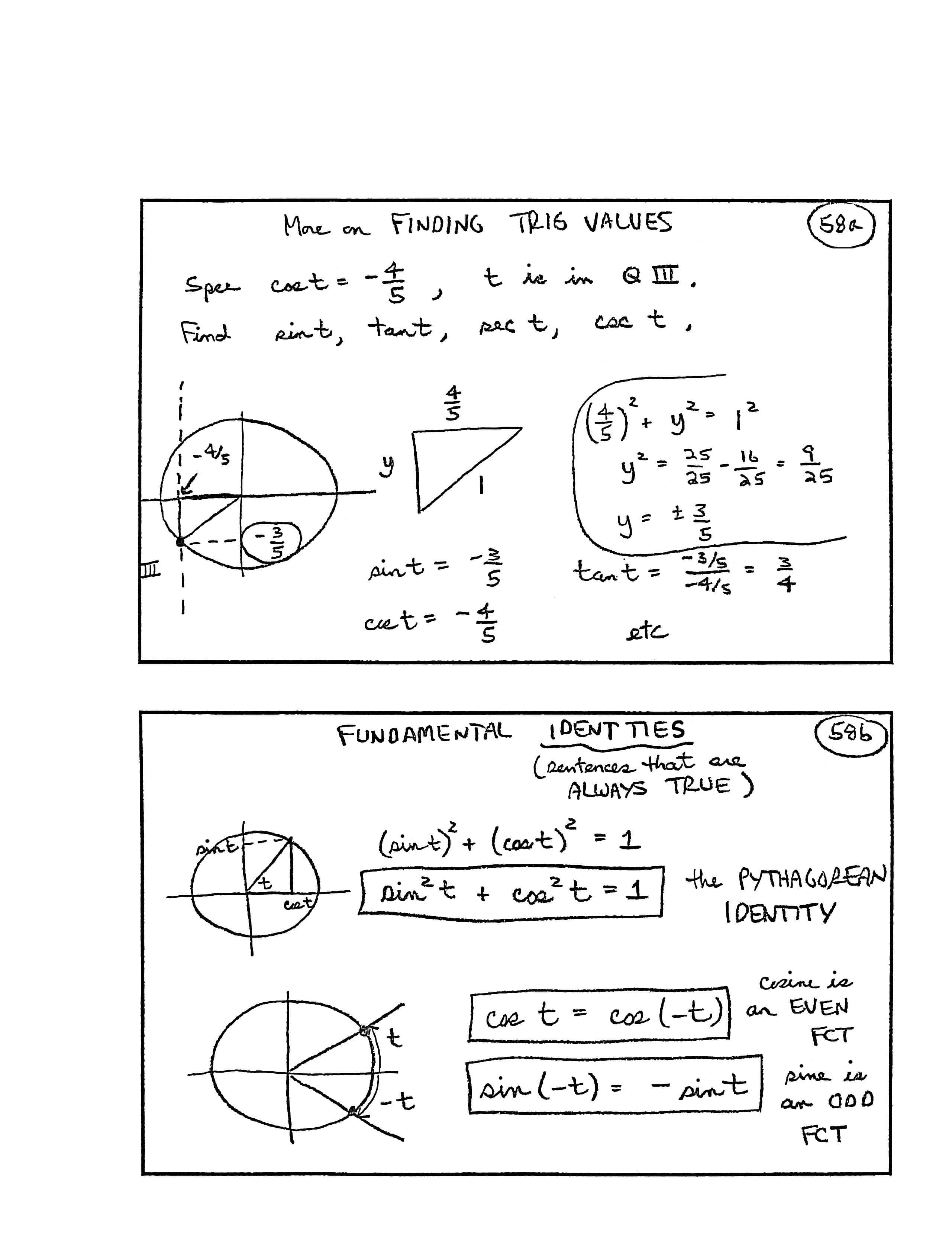
More on Finding Trig [trigonometric] Values
Spse [suppose] $\,\cos t = -\frac{4}{5}\,\,,$ $\,t$ is in Quadrant III.
Find $\,\sin t\,,$ $\,\tan t\,,$ $\,\sec t\,,$ $\csc t\,.$
[image: unit circle, with point $\,(-\frac 45,-\frac 35)\,$ plotted; the triangle in quadrant III is enlarged and labeled with side lengths $\,y\,,$ $\,\frac 45\,,$ and $\,1\,.$]
$$ \begin{gather} \left(\frac{4}{5}\right)^2 + y^2 = 1\cr \cr y^2 = \frac{25}{25} - \frac{16}{25} = \frac{9}{25}\cr \cr y = \pm\frac{3}{5} \end{gather} $$ $$ \begin{gather} \sin t = -\frac{3}{5}\cr \cr \cos t = -\frac{4}{5}\cr \cr \tan t = \frac{-3/5}{-4/5} = \frac{3}{4}\ \ \ \ \text{etc} \end{gather} $$Fundamental Identities (Sentences that are always true)
[image: unit circle with an angle $\,t\,$ and point $\,(\cos t\,,\,\sin t)\,$]
$$ \begin{gather} (\sin t)^2 + (\cos t)^2 = 1\cr \cr \sin^2 t + \cos^2 t = 1\cr \text{the Pythagorean Identity} \end{gather} $$[image: unit circle with angles $\,t\,$ and $\,-t\,$]
$$ \begin{gather} \cos t = \cos(-t)\cr \text{cosine is an EVEN function}\cr \cr \sin(-t) = -\sin t\cr \text{sine is an ODD function} \end{gather} $$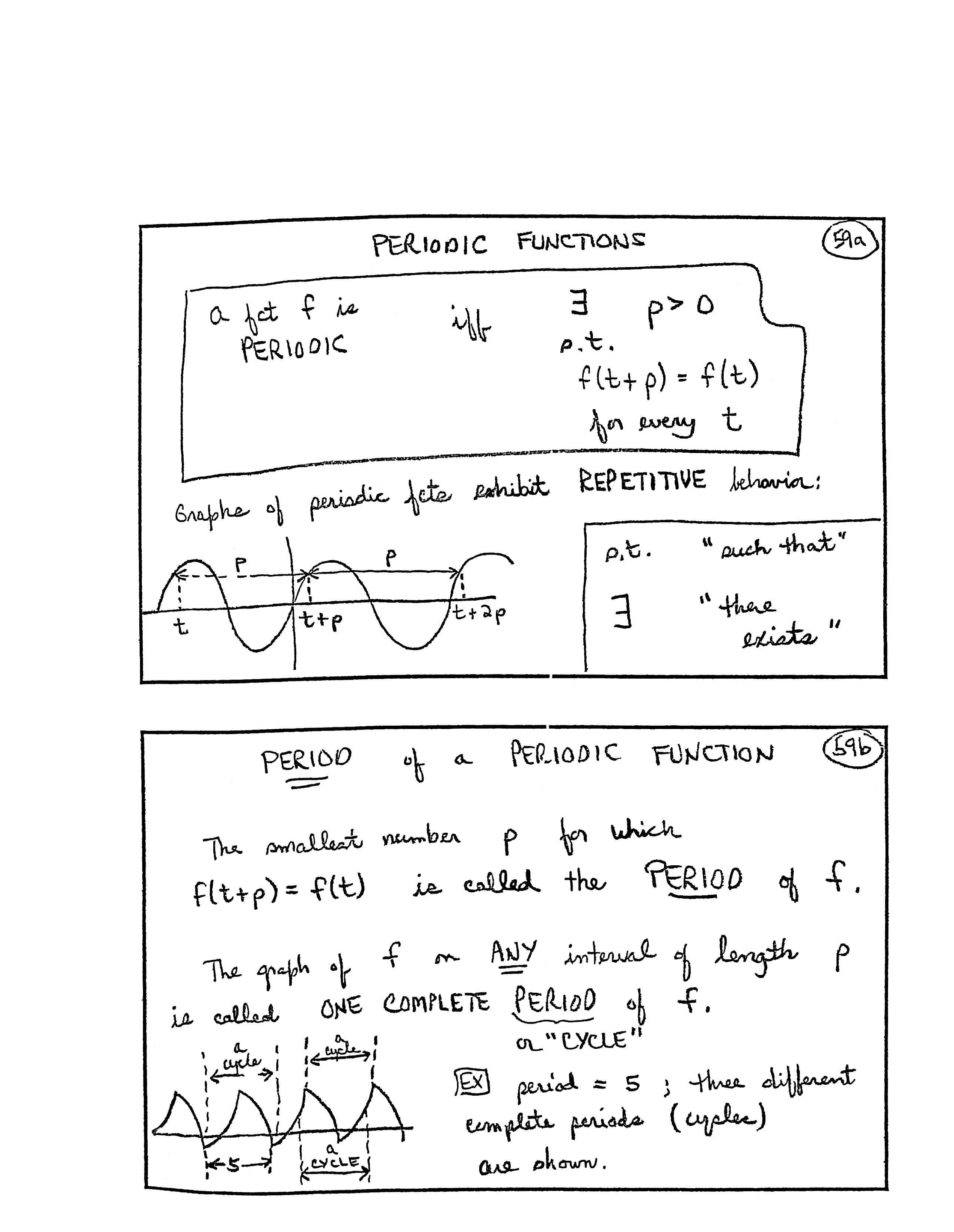
(This section gives a more advanced definition of periodic function than this index card.)
The Period of a Periodic Function
Periodic Functions
| A fct [function] $\,f\,$ is PERIODIC | iff [if and only if] | $\exists\ \ p \gt 0\,$ s.t. $\,f(t + p) = f(t)\,$ for every $\,t$ |
| s.t. | “such that” |
| $\exists$ | “there exists” |
Graphs of periodic fcts [functions] exhibit REPETITIVE behavior:
[image: graph of a periodic function, showing the same function value at $\,t\,,$ $\,t + p\,,$ and $\,t + 2p$]
Period of a Periodic Function
The smallest number $\,p\,$ for which $\,f(t + p) = f(t)\,$ is called the PERIOD of $\,f\,.$
The graph of $\,f\,$ on any interval of length $\,p\,$ is called one complete period (or “cycle”) of $\,f\,.$
[image: a periodic function with period $\,5\,,$ showing three different periods (cycles)]
EX [example]: period $\,= 5\,$; three different complete periods (cycles) are shown
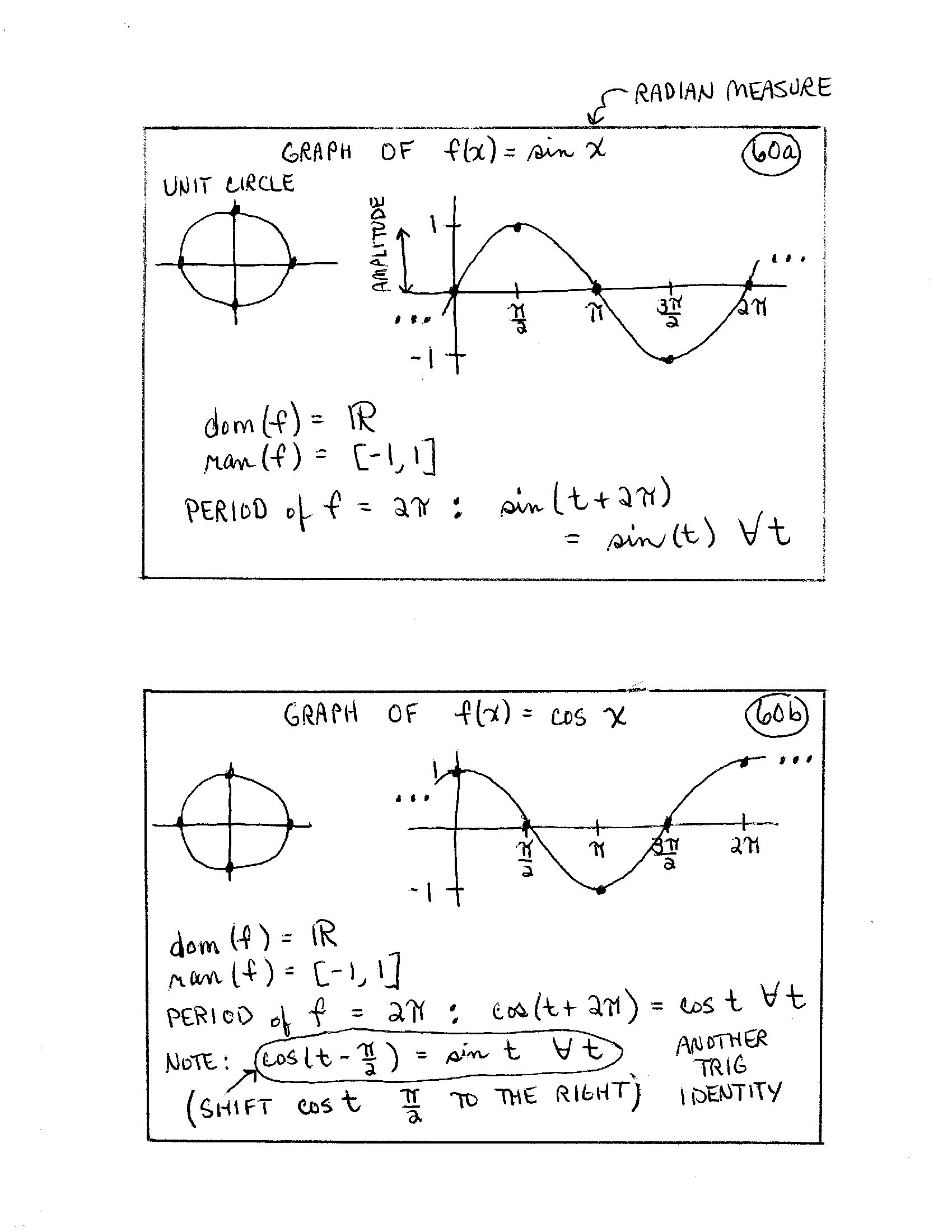
Graph of $\,f(x) = \sin \underbrace{x}_{\substack{\text{radian}\\ \text{measure}}}$
[Unit circle, showing points used to get graph]
[Plot the points $\,(\text{radian measure of angle},\text{$y$-value of point})\,$: $\,(0,0)\,,$ $\,(\frac\pi 2,1)\,,$ $\,(\pi,0)\,,$ $\,(\frac{3\pi}2,-1)\,,$ and $\,(2\pi,0)$]
$$ \begin{gather} \text{dom}(f) = \mathbb{R}\cr \cr \text{ran}(f) = [-1,1] \end{gather} $$Period of $\,f\,$ $\,= 2\pi\,$: $$\sin(t + 2\pi) = \sin t \quad \forall\, t$$
[Recall: $\,\forall = \text{for all}$]
Graph of $\,f(x) = \cos x$
[Unit circle, showing points used to get graph]
[Plot the points $\,(\text{radian measure of angle},\text{$x$-value of point})\,$: $\,(0,1)\,,$ $\,(\frac\pi 2,0)\,,$ $\,(\pi,-1)\,,$ $\,(\frac{3\pi}2,0)\,,$ and $\,(2\pi,1)$]
$$ \begin{gather} \text{dom}(f) = \mathbb{R}\cr \cr \text{ran}(f) = [-1, 1] \end{gather} $$Period of $\,f\,$ $\,= 2\pi\,$: $$\cos(t + 2\pi) = \cos t \quad \forall\, t$$
Note:
$$ \cos(t - \frac{\pi}{2}) = \sin t \quad \forall\, t $$(Another trig [trigonometric] identity: shift $\,\cos t\,,$ $\,\frac{\pi}{2}\,$ to the right)
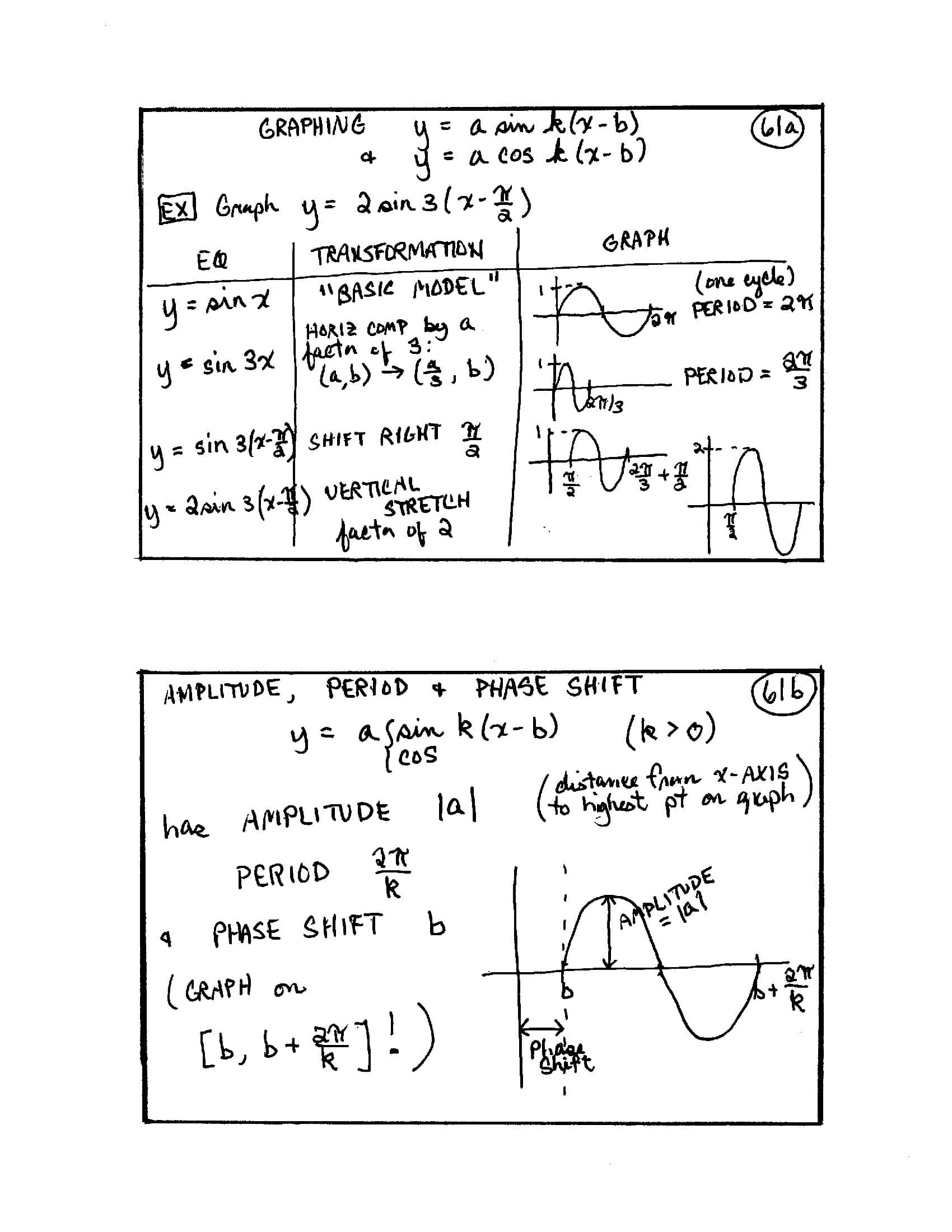
Graphing Generalized Sine and Cosines (Part 2)
Amplitude, Period, and Phase Shift
Given Amplitude, Period, and Phase Shift, Write an Equation
GRAPHING $\,y = a \sin k(x - b)\,$ and $\,y = a \cos k(x - b)$
EX [Example]: Graph $\,y = 2 \sin 3\left(x - \frac{\pi}{2}\right)$
[Note: Only one cycle of each curve is shown in each graph of this example.]
| EQ | TRANSFORMATION | GRAPH |
|---|---|---|
| $y = \sin x$ | “Basic model” | (one cycle) PERIOD $\,= 2\pi$ |
| $y = \sin 3x$ | Horiz Comp [horizontal compression] by a factor of $\,3\,$: $\,(a,b) \to \left(\frac{a}{3}, b\right)$ | PERIOD $\,= \frac{2\pi}{3}$ |
| $y = \sin 3\bigl(x - \frac{\pi}{2}\bigr)$ | Shift right $\,\frac{\pi}{2}$ | [cycle begins at $\,\frac\pi 2\,$ and ends at $\,\frac{2\pi}3 + \frac\pi 2\,$] |
| $y = 2\sin 3\bigl(x - \frac{\pi}{2}\bigr)$ | Vertical stretch, factor of $\,2$ | [same as prior graph, except amplitude is now $\,2\,$] |
AMPLITUDE, PERIOD & PHASE SHIFT
$$ \begin{gather} y = a \sin k(x - b)\cr \ \ \text{or}\cr y = a \cos k(x - b)\ ,\cr k \gt 0 \end{gather} $$[Each of these curves...] has:
AMPLITUDE $\,|a|\,$
(distance from
$x$-axis
to highest pt [point] on graph)
PERIOD $\,\frac{2\pi}{k}$
and PHASE SHIFT $\,b$
(Graph on $\left[b\,, \, b + \frac{2\pi}{k}\right]\,$! )
[Graph: Both ‘Phase Shift’ and ‘Amplitude $\,= |a|\,$’ are labeled. Shows one cycle of $\,y = a\sin k(x-b)\,,$ starting at $\,x = b\,$ and ending at $\,x = b + \frac{2\pi}k\,.$]
[Note that when $\,x = b\,,$ we have $\,k(x-b) = k(b-b) = 0\,,$ and when $\,x = b + \frac{2\pi}k\,,$ we have: $$ \begin{align} k(x-b) &= k(b + \frac{2\pi}k - b)\cr &= k(\frac{2\pi}k)\cr &= 2\pi\ \ \ ] \end{align} $$
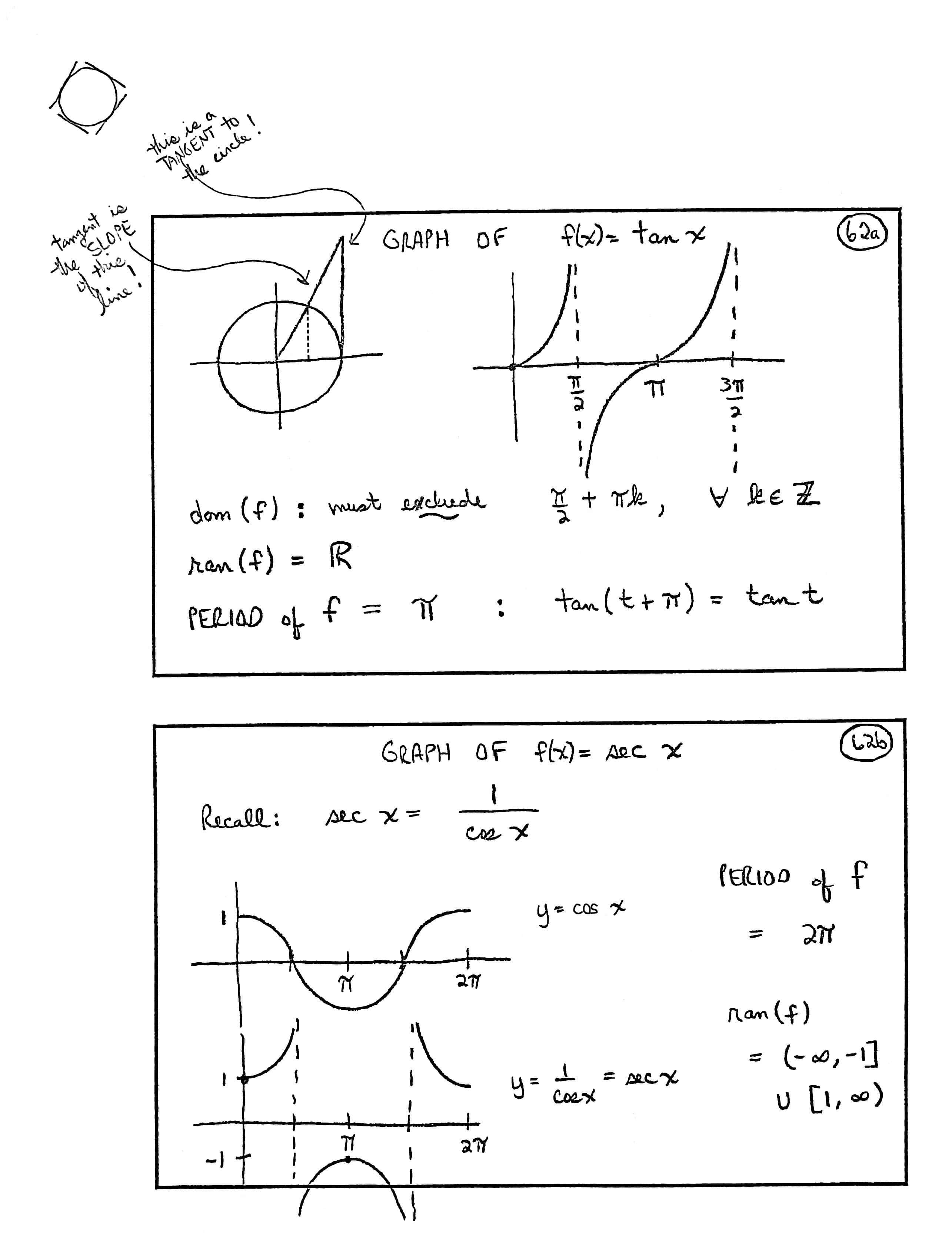
GRAPH OF $\,f(x) = \tan x$
[Upper left corner: some tangents to a circle are shown]
[Image: Unit circle, showing an angle laid off with two important related line segments.
If the angle laid off is $\,x\,,$
then the slope of the diagonal segment is $\,\tan x\,.$
The length of the vertical segment (which is a tangent to the circle) is the size of
$\,\tan x\,.$
Why? Call the length of the (solid) vertical segment $\,y\,.$ Then, by similar triangles,
$\,\frac{\sin x}{\cos x} = \frac{y}{1}\,,$
and solving for $\,y\,$ gives $\,y = \frac{\sin x}{\cos x} = \tan x\,.$]
[Graph of $\,y = \tan x\,.$ Note that the vertical dashed lines $\,x = \frac{\pi}2\,$ and $\,x = \frac{3\pi}2\,$ are vertical asymptotes for the graph.]
$\text{dom}(f)\,$ [domain of $\,f\,$]: must exclude
$\,\frac\pi 2 + \pi k\,,\ \ \forall\ \ k\in\Bbb Z$
[Recall: ‘$\,\forall\,$’ is ‘for all’ and $\,\Bbb Z\,$ is the set of integers]
$\text{ran}(f) = \Bbb R\,$
[Recall: $\,\text{ran}(f)\,$ is ‘range of $\,f\,$’
and $\,\Bbb R\,$ is the set of real numbers]
Period of $\,f = \pi\,$ : $\,\tan(t + \pi) = \tan t$
GRAPH OF $\,f(x) = \sec x$
Recall: $\displaystyle\,\sec x = \frac{1}{\cos x}$[Graphs, aligned one atop the other, of $\,y = \cos x\,$ and its reciprocal, $\,y = \frac{1}{\cos x}\,.$ Note that where the $y$-value of $\,y = \cos x\,$ is zero, then there is no point (in this case, a vertical asymptote) on the graph of $\,y = \frac1{\cos x}\,.$ Also note that the reciprocal of $\,1\,$ is $\,1\,,$ and the reciprocal of $\,-1\,$ is $\,-1\,.$]
Period of $\ f = 2\pi$
$\text{ran}(f) = (-\infty, -1] \cup [1, \infty)$

LENGTH of a CIRCULAR ARC
[Image: shows a central angle $\,\theta\,$ in a circle with radius $\,r\,$; the subtended arc is $\,s\,$]
$$ s = r\theta\,, $$when $\,\theta\,$ is a CENTRAL ANGLE given in RADIAN measure.
Pf [Proof]:
$$ \begin{gather} \bcancel{\cancel{\frac{\theta}{2\pi} = \frac{s}{2\pi r}}}\cr\cr \text{($\,2\pi r\,$: circumference of circle}\cr \text{with radius $\,r\,$)}\cr\cr \theta \cancel{2\pi} r = s \cancel{2\pi} \end{gather} $$Why the name “RADIAN MEASURE”?
Rewrite $\,s = r\theta\,$ as:
$$ \underbrace{\theta}_{\substack{\text{RADIAN measure}\cr \text{of an angle}}} = \underbrace{\frac s r}_{\substack{\text{How many “$r$” 's}\cr \text{are there in “$s$”?}}} $$[image: an angle with radian measure $\,2\,,$ since it takes $\,2\,$ radiuses to fill up the arc that subtends the angle]
The radian measure of $\,\theta\,$ is the number of ‘radiuses’ that can fit in the arc that subtends $\,\theta\,$; hence the term RADian (“RADiuses IN”).

AREA of a CIRCULAR SECTOR
[image: a circle with central angle $\,\theta\,$ and radius $\,r\,$, with the sector shaded]
$$ A = \frac 12 r^2\theta\,,$$where $\,\theta\,$ is given in RADIAN measure.
Pf [Proof]:
$$ \begin{gather} \bcancel{\cancel{\frac A{\pi r^2} = \frac{\theta}{2\pi}}}\cr\cr A\cdot 2\pi = \theta\cdot \pi r^2\cr\cr A = \frac 12 r^2\theta \end{gather} $$Note: $\,\pi r^2\,$ is the area of circle w/ [with] radius $\,r\,$
EXAMPLE
A sector of a circle has a central angle of $\,60^\circ\,.$ Find the area of the sector if the radius of the circle is $\,3\,$ miles.
[image: circle with central angle $\,60^\circ\,$ and radius $\,3\,$ miles. Each square shown is about $\,1\,$ square mile.]
$$ 60^\circ = 60^\circ \cdot \frac{\pi \,\text{rad}}{180^\circ} = \frac{\pi}{3} \,\text{rad} $$$$ \begin{align} A &= \frac{1}{2} r^{2} \theta\cr\cr &= \frac{1}{2} (3^{2})\left(\frac{\pi}{3}\right)\cr\cr &= \frac{3}{2}\pi\ \ \ \text{square miles}\cr\cr &\approx 4.7 \ \text{mi}^2 \end{align} $$
Believable!!

RIGHT TRIANGLE TRIGONOMETRY
[image: a typical right triangle with an angle $\,\theta\,$ labeled. The sides are: adjacent (ADJ), opposite (OPP) and hypotenuse (HYP).]
$\,\sin \theta = \frac{\text{OPP}}{\text{HYP}}\, $
$\,\cos \theta = \frac{\text{ADJ}}{\text{HYP}}\, $
$\,\tan \theta = \frac{\text{OPP}}{\text{ADJ}}\, $
$\,\cot \theta\,$
$\,\sec \theta\,$
$\,\csc \theta\,$
Note:
$\sin\theta\,$ and $\,\csc\theta\,$ are reciprocals.
$\cos\theta\,$ and $\,\sec\theta\,$ are reciprocals.
$\tan\theta\,$ and $\,\cot\theta\,$ are reciprocals.
USING THE RIGHT $\,\Delta\,$ [triangle] DEFINITIONS
EX [example]: Spse [suppose] $\,\cos \theta = \frac{1}{5}\,$ and spse $\,\theta\,$ is in Quadrant I. Find $\,\sin \theta\,$ and $\,\tan \theta\,.$
[image: a right triangle with angle $\,\theta\,,$ adjacent side $\,1\,,$ hypotenuse $\,5\,,$ and opposite side $\,x\,$]
$$ \begin{gather} 1^{2} + x^{2} = 5^{2}\cr x^{2} = 24\cr x = \sqrt{24} = \sqrt{4 \cdot 6} = 2\sqrt{6}\cr\cr \sin \theta = \frac{2\sqrt{6}}{5}\,,\cr \tan \theta = \frac{2\sqrt{6}}{1} = 2\sqrt{6} \end{gather} $$EX: Solve the right triangle. (Find all sides and angles.)
[image: right triangle with a $\,75^\circ\,$ angle, sides $\,x\,$ and $\,100\,.$ The remaining angle must be $\,15^\circ\,.$]
$$ \begin{gather} \sin 75^\circ = \frac{100}{\text{HYP}}\cr \strut\text{so}\cr \text{HYP} = \frac{100}{\sin 75^\circ} \approx 103.53\cr \strut\text{(Store!!)}\cr\cr x^{2} + 100^{2} = \text{HYP}^{2}\,,\cr \text{so}\ \ x \approx 26.79 \end{gather} $$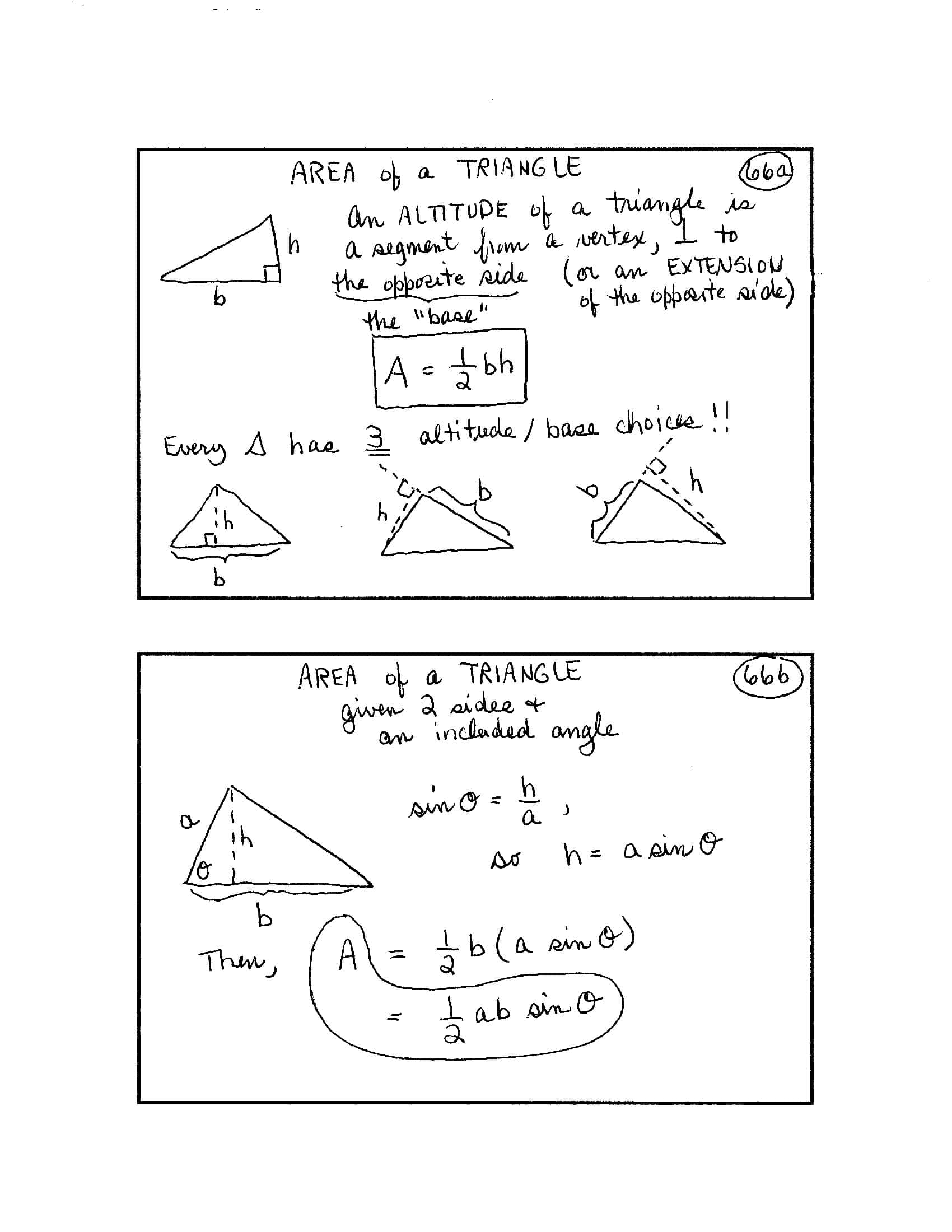
AREA of a TRIANGLE
[image: a right triangle with altitude $\,h\,$ and base $\,b\,$]
An altitude of a triangle is a segment from a vertex, $\,\perp\,$ [perpendicular] to the opposite side (the “base”) (or an extension of the opposite side).
$$ A = \frac{1}{2} b h $$Every $\,\Delta\,$ [triangle] has $\,3\,$ altitude/base choices!!
[images: three copies of the same triangle, showing the three altitude/base pairs]
AREA of a TRIANGLE (given $\,\bf 2\,$ sides & an included angle)
[image: a triangle with two sides $\,a\,$ and $\,b\,$ and included angle $\,\theta\,$; the altitude corresponding to base $\,b\,$ is labeled as $\,h\,$]
$$ \sin \theta = \frac{h}{a}\,,\ \ \text{so}\ \ h = a \sin \theta $$Then,
$$ \begin{align} A &= \frac{1}{2} b (a \sin \theta)\cr\cr &= \frac{1}{2} ab \sin \theta \end{align} $$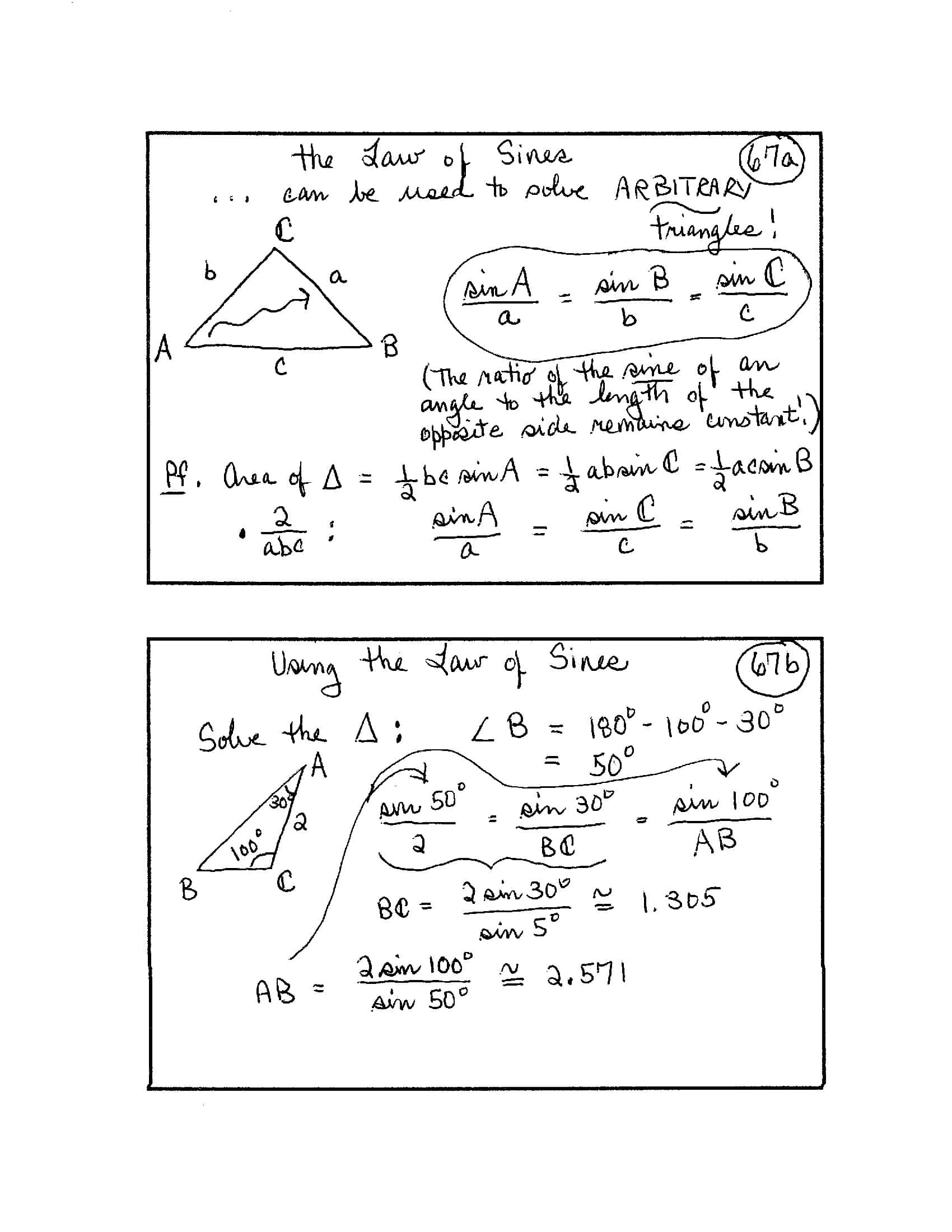
The Law of Sines
... can be used to solve ARBITRARY triangles!
[image: an arbitrary triangle: side $\,a\,$ is opposite angle $\,A\,,$ side $\,b\,$ is opposite angle $\,B\,,$ side $\,c\,$ is opposite angle $\,C\,$]
$$ \frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c} $$(The ratio of the sine of an angle to the length of the opposite side remains constant!)
Pf [proof]:
$$ \begin{align} \text{Area of } \Delta &= \frac{1}{2} b c \sin A\cr\cr &= \frac{1}{2} a b \sin C\cr\cr &= \frac{1}{2} a c \sin B \end{align} $$Multiply by $\displaystyle\,\frac 2{abc}\,$:
$$ \frac{\sin A}{a} = \frac{\sin C}{c} = \frac{\sin B}{b} $$Using the Law of Sines
Solve the $\,\Delta\,$ [triangle]:
[image: a triangle with two given angles, $\,110^\circ\,$ and $\,30^\circ\,,$ and a side of length $\,2\,$ between these two given angles]
$$ \angle B = 180^\circ - 100^\circ - 30^\circ = 50^\circ $$ $$ \frac{\sin 50^\circ}{2} = \frac{\sin 30^\circ}{BC} = \frac{\sin 100^\circ}{AB} $$[Note: $\,AB\,$ denotes the distance from $\,A\,$ to $\,B\,$]
$$ \begin{gather} BC = \frac{2 \sin 30^\circ}{\sin 50^\circ} \approx 1.305\cr\cr AB = \frac{2 \sin 100^\circ}{\sin 50^\circ} \approx 2.571 \end{gather} $$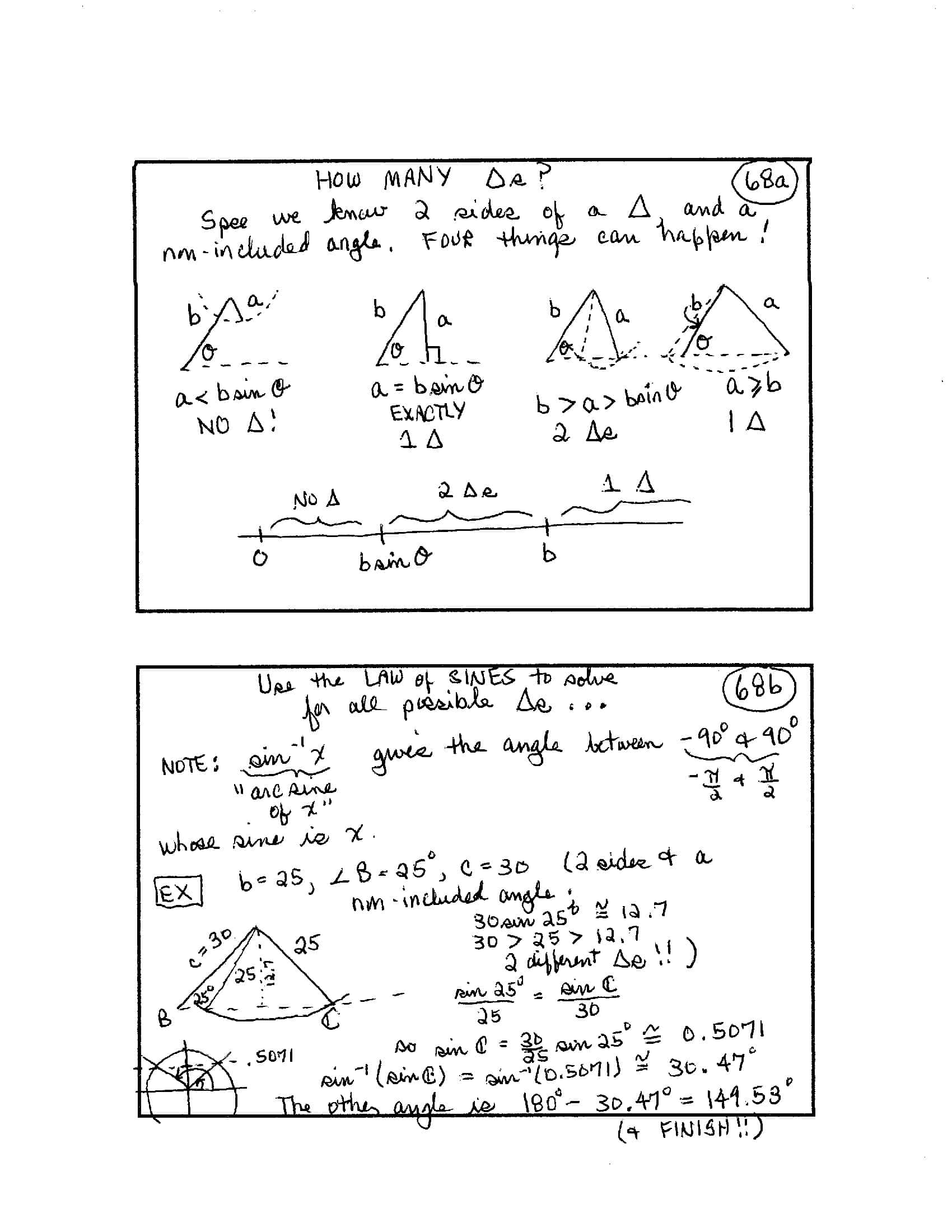
Given Two Sides and a Non-Included Angle, How Many Triangles? (Part 2)
How Many $\Delta$s [triangles]?
Suppose we know $\,2\,$ sides of a $\,\Delta\,$ [triangle] and a non-included angle. Four things can happen!
[images: Given a side $\,b\,$ and angle $\,\theta\,,$ attach another side $\,a\,.$ If $\,a\,$ is too short and you sweep it around, it will never hit the dashed line that forms the angle $\,\theta\,$ to make a triangle. Keep making $\,a\,$ longer and longer to see what happens!
- $\,a \lt b \sin \theta\,$
NO $\Delta\,$ [triangle]! - $\,a = b \sin \theta\,$
EXACTLY $\,1\, \Delta$ - $\,b \gt a \gt b \sin \theta\,$
$\,2\,\Delta$s - $\,a \ge b\,$
$\,1\,\Delta$
[Number line diagram shows intervals for NO $\Delta\,,$ $\,2\, \Delta$s, $\,1\, \Delta\,$]
Use the Law of Sines to solve for all possible $\Delta$s ...
NOTE: $\,\sin^{-1} x\,$ (arcsine of $\,x\,$) gives the angle between $\,-90^\circ\,$ and $\,90^\circ\,$ ($\,\frac{\pi}{2}\,$ and $\,\frac{\pi}{2}\,$) whose sine is $\,x\,.$
EX [example]: $\,b = 25,\ \angle B = 25^\circ,\ c = 30\,$
($\,2\,$ sides and a non-included angle;
$30 \sin 25^\circ \approx 12.7$
$30 \gt 25 \gt 12.7$
$2\,$ different $\,\Delta$s!!)
[image summarizing the given information]
$$ \begin{gather} \frac{\sin 25^\circ}{25} = \frac{\sin C}{30}\cr\cr \text{so }\ \sin C = \frac{30}{25}\sin 25^\circ \approx 0.5071\cr\cr \sin^{-1}(\sin C) = \sin^{-1}(0.5071) \approx 30.47^\circ \end{gather} $$The other angle is
$$180^\circ - 30.47^\circ = 149.53^\circ$$(and FINISH!!)
[image shows that there are TWO angles between $\,0^\circ\,$ and $\,180^\circ\,$ that have sine equal to $\,0.5071\,$]

The Law of Cosines
(useful when you know $\,2\,$ sides and an included angle)
[images: three triangles; when angle $\,A\,$ is obtuse, $\,\cos A\lt 0\,$; when $\,A\,$ is a right angle, $\,\cos A = 0\,$; when $\,A\,$ is acute, $\,\cos A\gt 0\,$]
$$a^{2} = b^{2} + c^{2} - 2bc \cos A$$$-2bc\cos A\,$ is an “adjustment” for when you don’t have a right $\,\Delta\,$ [triangle]!
- $-2bc\cos A = 0\,$ when $\,A = 90^\circ$
- $-2bc\cos A\,$ is POSITIVE when $\,A\,$ is obtuse
- $-2bc\cos A\,$ is NEGATIVE when $\,A\,$ is acute
Be able to state all $\,3\,$ versions!
[Here are the other two versions:]
$$ \begin{gather} b^2 = a^2 + c^2 - 2ac\cos B\cr\cr c^2 = a^2 + b^2 - 2ab\cos C \end{gather} $$Proving the Law of Cosines
... is an easy application of the Distance Formula!
[image: an arbitrary triangle, with vertex $\,A\,$
at the origin and side $\,c\,$ along the
$x$-axis.
Vertex $\,A\,$ has coordinates $\,(0,0)\,.$
Vertex $\,B\,$ has coordinates $\,(c,0)\,.$
Vertex $\,C\,$ has coordinates $\,(b\cos A,b\sin A)\,.$]
[Use the Distance Formula to find the square of the distance from $\,C(b\cos A,b\sin A)\,$ to $\,B(c,0)\,$]
$$ \begin{align} a^{2} &= (b \cos A - c)^{2} + (b \sin A - 0)^{2}\cr &= b^{2} \cos^{2} A - 2bc \cos A + c^{2} + b^{2} \sin^{2} A\cr &= b^{2}(\overbrace{\cos^{2} A + \sin^{2} A}^{= 1}) + c^{2} - 2bc \cos A\cr &= b^{2} + c^{2} - 2bc \cos A \end{align} $$Verbalize: In any triangle: a side squared is the sum of the squares of the other two sides, minus twice the product of these other two sides, times the cosine of the included angle.
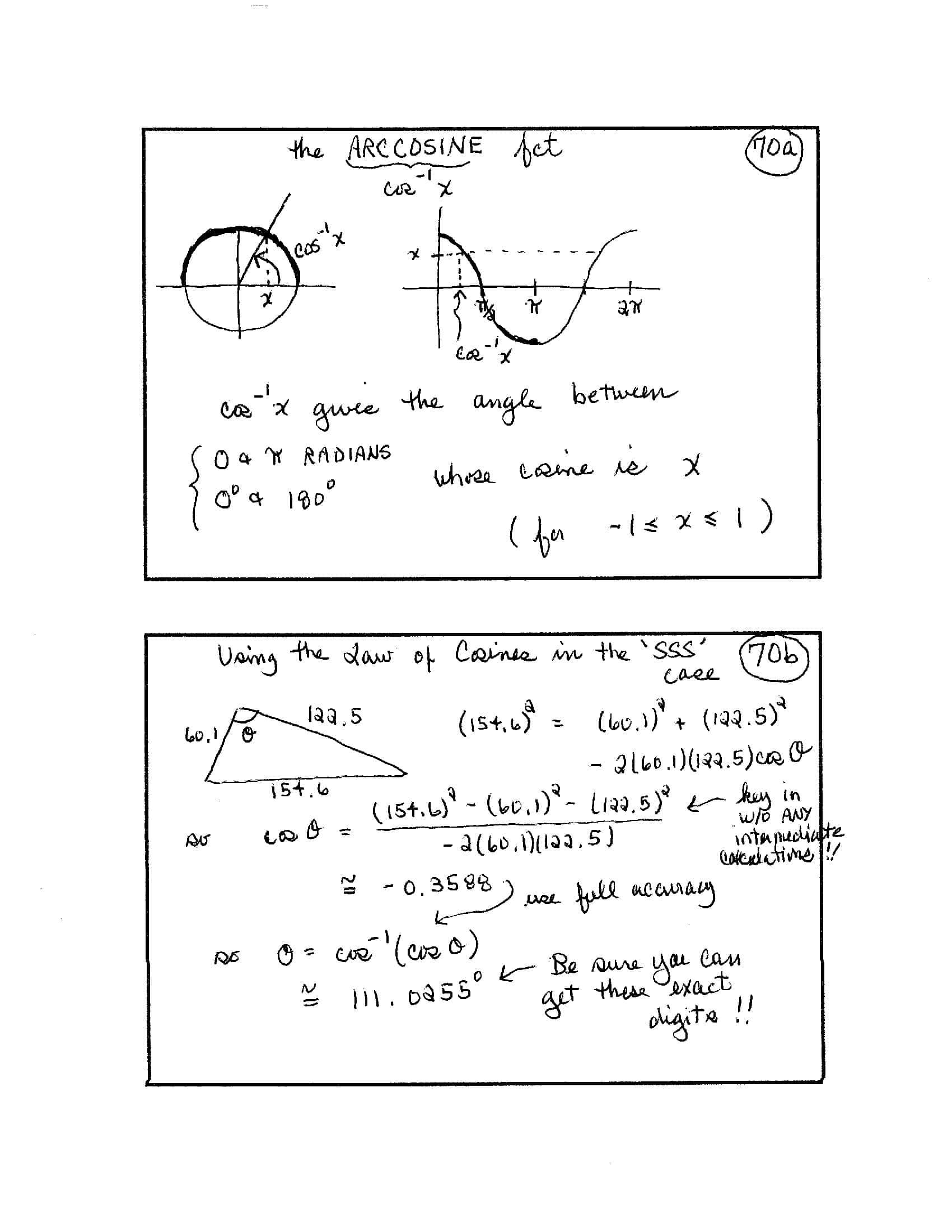
the $\,\underbrace{\text{ARCCOSINE}}_{\cos^{-1}x}\,$ Function
[image: unit circle, showing a number $\,x\,$ and the angle $\,\cos^{-1}x\,$]
[image: graph of $\,y = \cos x\,$ on the interval $\,[0,2\pi]\,$; showing a number $\,x\,$ and the (radian) angle $\,\cos^{-1}x\,$]
$\cos^{-1} x$ gives the angle between $\,0\,$ and $\,\pi\,$ radians (or between $\,0^\circ\,$ and $\,180^\circ\,$) whose cosine is $\,x\,$ (for $\,-1\le x\le 1\,$)
Using the Law of Cosines in the ‘SSS’ Case
[image: triangle with sides $\,154.6\,,$ $\,60.1\,,$ and $\,122.5\,$; the angle between $\,60.1\,$ and $\,122.5\,$ is labeled $\,\theta\,$]
$$ (154.6)^2 = (60.1)^2 + (122.5)^2 - 2(60.1)(122.5)\cos\theta $$so
$$ \begin{align} \cos\theta &= \overbrace{\frac{(154.6)^2 - (60.1)^2 - (122.5)^2}{-2(60.1)(122.5)}}^{\substack {\text{key in w/o [without] ANY}\\ \text{intermediate calculations}}}\cr\cr &\approx -0.3588 \end{align} $$so
$$ \begin{align} \theta &= \cos^{-1}(\cos\theta)\cr\cr &\approx \underbrace{111.0255^\circ}_{\substack{\text{Be sure you can get}\\ \text{these exact digits!!}}} \end{align} $$
Using the Law of Sines & Law of Cosines Together
Remember: In any triangle, the longest side is opposite the largest angle; the shortest side is opposite the smallest angle.
When using the Law of Sines—BE CAREFUL! Make sure this is satisfied!! Use ACUTE angles whenever possible!!
Do all calculations using the FULL ACCURACY of your calculator; only ROUND when reporting your final answers.
Example
[image: triangle with two known sides (lengths $\,10.5\,$ and $\,18\,$) and an included angle $\,46.5^\circ\,.$]
Solve the $\,\Delta\,$ [triangle].
$$ z^2 = (10.5)^2 + 18^2 - 2(10.5)(18)\cos 46.5^\circ $$so $\,z\approx 13.1929\,.$
INCORRECT:
$$ \begin{gather} \frac{\sin 46.5^\circ}{z} = \frac{\sin A}{18}\cr\cr \text{so}\cr\cr \sin A = \frac{18 \sin 46.5^\circ}{z} \approx 0.9847\cr\cr \text{so}\cr\cr \bcancel{\cancel{A = \sin^{-1}(\sin A) \approx 81.76^\circ}} \end{gather} $$Actually:
$$A = 180^\circ - 81.76^\circ = 98.24^\circ$$CORRECT:
$$ \begin{gather} \frac{\sin 46.5^\circ}{z} = \frac{\sin B}{10.5}\cr\cr \text{so}\cr\cr \sin B = \frac{10.5 \sin 46.5^\circ}{z} \approx 0.5773\cr\cr \text{so}\cr\cr B = \sin^{-1}(0.5773) \approx 35.26^\circ \end{gather} $$So:
$$ A = 180^\circ - 35.26^\circ - 46.5^\circ = 98.24^\circ $$
Verifying Trigonometric Identities: 2 Basic Approaches
(Note: To prove that something is not an identity, just provide a single # [number] for which it is not true.
[Approach 1: Try this when one side of the identity
is complicated, and the other side is simpler.
Transform the complicated side into the simpler side.]
COMPLICATED = SIMPLER
(Transform one side into other side)
[Approach 2: Try this when both sides of the
identity are equally complicated. Transform both
sides into the same
simpler expression.]
COMPL$1$ = COMPL$2$
[Complicated$1$ = Complicated$2$]
Identities You Must Know!
[Stack the six trigonometric functions in this order; then the lines shown connect reciprocals!]
$$ \begin{gather} \sin\cr\cr \cos\cr\cr \tan = \frac{\sin}{\cos}\cr\cr \cot = \frac{\cos}{\sin}\cr\cr \sec = \frac{1}{\cos}\cr\cr \csc = \frac{1}{\sin} \end{gather} $$ $$ \begin{gather} \sin^2 + \cos^2 = 1\cr [\div \text{ both sides by } \cos^2 \text{ to get:}]\cr \tan^2 + 1 = \sec^2\cr\cr \sin^2 + \cos^2 = 1\cr [\div \text{ both sides by } \sin^2 \text{ to get:}]\cr 1 + \cot^2 = \csc^2 \end{gather} $$ $$ \begin{align} \tan(-x) &= \frac{\sin(-x)}{\cos(-x)}\cr\cr &= \frac{-\sin(x)}{\cos(x)}\cr\cr &= -\tan(x) \end{align} $$
Transforming More Complicated Side into Simpler Side
Verify this identity:
$$ \csc x \,(\csc x + \sin(-x)) = \cot^{2} x $$$$ \begin{align} &\csc x (\csc x + \sin(-x))\cr &\quad = \csc^{2} x + \csc x \,\sin(-x)\cr &\quad = 1 + \cot^{2} x + \frac{1}{\sin x}(-\sin x)\cr &\quad = 1 + \cot^{2} x - 1\cr &\quad = \cot^{2} x \end{align} $$
One CMS (Complete Mathematical Sentence) is REQUIRED!!
Working with Both Sides Separately
Verify the identity:
$$ \frac{1 + \cos \theta}{\cos \theta} = \frac{\tan^{2} \theta}{\sec \theta - 1} $$[Note: LHS = Left Hand Side and RHS = Right Hand Side. Also, $\,\sec\theta + 1\,$ means $\,(\sec\theta) + 1\,.$]
$$ \begin{align} \text{LHS} &= \frac{1 + \cos \theta}{\cos \theta}\cr\cr &= \frac{1}{\cos \theta} + \frac{\cos \theta}{\cos \theta}\cr\cr &= \color{red}{\sec \theta + 1} \end{align} $$$$ \begin{align} \text{RHS} &= \frac{\tan^{2} \theta}{\sec \theta - 1} \cdot\frac{\sec\theta + 1}{\sec\theta + 1}\cr\cr &= \frac{\tan^{2} \theta \,(\sec \theta + 1)}{\sec^2 \theta - 1}\cr\cr &= \frac{\cancel{\tan^{2} \theta} \, (\sec \theta + 1)}{\cancel{\tan^{2} \theta}}\cr\cr &= \color{red}{\sec \theta + 1} \end{align} $$
SAME!

Addition & Subtraction Formulas
$$ \sin(A \color{red}{\pm} B) = \sin A \cos B \color{red}{\pm} \cos A \sin B $$[Note: This is a shorthand for TWO formulas:] $$ \begin{gather} \sin(A + B) = \sin A \cos B + \cos A\sin B\cr \text{and}\cr \sin(A - B) = \sin A \cos B - \cos A\sin B \end{gather} $$
[Note: ‘Sine, same’:
for the SINE, the
‘$\,\pm\,$’ in ‘$\,\sin(A\pm B)\,$’
is the SAME as the
‘$\,\pm\,$’ in
‘$\,\sin A \cos B \pm \cos A \sin B\,.$’
Notice
that for the cosine formulas, one side has $\,\pm\,$
but the other side has $\,\mp\,.$]
(Not trivial to prove!)
Finding Exact Values
(Write as sums/differences of special angles)
[images: the unit circle and special triangles used to find the sine/cosine of special angles]
$$ \begin{align} &\cos 165^\circ\cr\cr &\quad = \cos(90^\circ + 75^\circ)\cr\cr &\quad = \cos 90^\circ \cos 75^\circ - \sin 90^\circ \sin 75^\circ\cr\cr &\quad = 0 - (1)\sin 75^\circ\cr\cr &\quad = -\sin(45^\circ + 30^\circ)\cr\cr &\quad = -(\sin 45^\circ \cos 30^\circ + \cos 45^\circ \sin 30^\circ)\cr\cr &\quad = -\Big(\frac{1}{\sqrt{2}} \cdot \frac{\sqrt{3}}{2} + \frac{1}{\sqrt{2}} \cdot \frac{1}{2}\Big)\cr\cr &\quad = \frac{-1 - \sqrt{3}}{2\sqrt{2}} \end{align} $$
Double-Angle Formulas
$$ \sin 2x = 2 \sin x \cos x $$ $$ \begin{align} \cos 2x &= \cos^{2}x - \sin^{2}x\cr &= 1 - 2 \sin^{2}x\cr &= 2 \cos^{2}x - 1 \end{align} $$Be able to derive all these formulas! (Write $\,2x = x + x\,$ and use sum formulas.)
Example
Given that $\,\cos x = \frac{4}{5}\,$ and $\,\csc x \lt 0\,,$ find $\,\sin 2x\,,$ $\,\cos 2x\,,$ and $\,\tan 2x\,.$
SOLN [Solution]: $\csc x = \frac{1}{\sin x}\,,$ so $\,\csc x \lt 0 \ \Rightarrow\ \sin x \lt 0$
[images: unit circle, with $\,\frac 45\,$ marked on $x$-axis and desired angle $\,x\,$ shown; the ‘right triangle’ view of this situation]
$$ \begin{align} \sin 2x &= 2 \sin x \cos x \cr\cr &= 2 \bigl(\frac{-3}{5}\bigr)\bigl(\frac{4}{5}\bigr)\cr\cr &= -\frac{24}{25} \end{align} $$$$ \begin{align} \cos 2x &= 2 \cos^{2}x - 1\cr\cr &= 2 \bigl(\frac{4}{5}\bigr)^{2} - 1\cr\cr &= 2\cdot\frac{16}{25} - \frac{25}{25}\cr\cr &= \frac{7}{25} \end{align} $$
$$ \begin{align} \tan 2x &= \frac{\sin 2x}{\cos 2x}\cr\cr &= \frac{-24/25}{7/25}\cdot \frac{25}{25}\cr\cr &= -\frac{24}{7} \end{align} $$
“Undoing” Trigonometric Functions
[images: graph of $\,y = \sin x\,,$ with the part of the graph on the interval $\,[-\frac\pi 2,\frac\pi 2]\,$ shaded; graph of $\,y = \cos x\,,$ with the part of the graph on the interval $\,[0,\pi]\,$ shaded]
The trig fcts [trigonometric functions] are not $\,1{-}1\,$ [one-to-one], hence do not have true inverses. In order to “undo” them, we must restrict each to an interval that covers all possible outputs, and on which the fct is $\,1{-}1\,.$
$$ \begin{gather} \text{sine:}\ \ [-\frac\pi 2,\frac\pi 2]\cr\cr \text{cosine:}\ \ [0,\pi] \end{gather} $$
If we know $\,\sin x = 0.5\,$
... can you tell me what $\,x\,$ is?
[image: graph of $\,y = \sin x\,,$ with $\,0.5\,$ marked on the $y$-axis, showing many different values of $\,x\,$ that get mapped to $\,0.5\,$]
NO!! $\,x\,$ could be any of the inputs shown...
(Note that only one of these lies between $\,-\frac{\pi}{2}\,$ and $\,\frac{\pi}{2}\,$; this is the one your calculator will give you!)
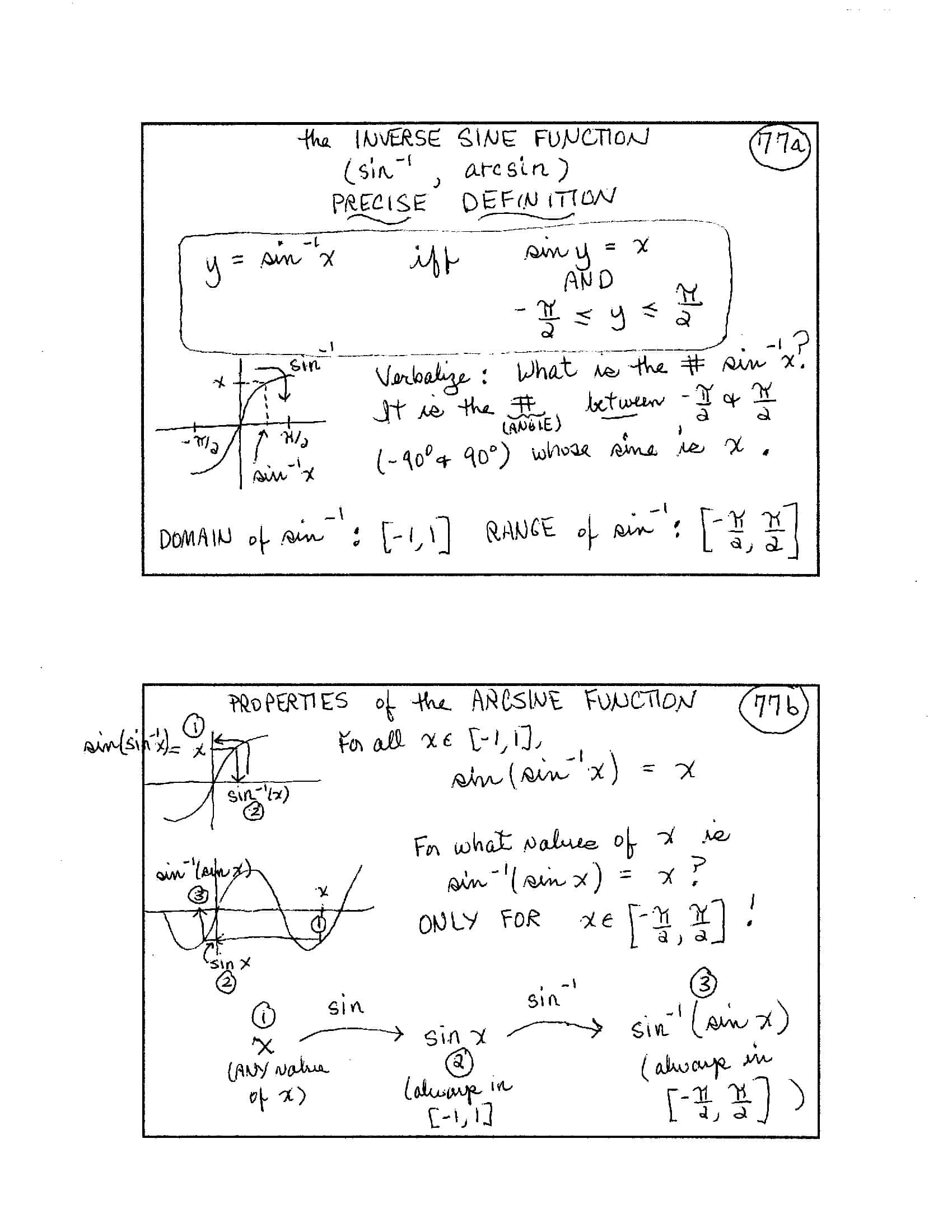
the INVERSE SINE FUNCTION
($\,\sin^{-1}\,,\ \ \arcsin\,$)
PRECISE DEFINITION
$$
\begin{gather}
y = \sin^{-1}x\cr
\text{iff}\cr
\bigl(\sin y = x\cr
\text{and}\cr
-\frac{\pi}{2} \le y \le \frac{\pi}{2}\bigr)
\end{gather}
$$
[image: partial graph of $\,y = \sin x\,$; start with $\,x\,$ between $\,-1\,$ and $\,1\,$ on the $y$-axis; the function $\,\sin^{-1}\,$ takes $\,x\,$ to $\,\sin^{-1} x\,,$ which is between $\,-\frac\pi 2\,$ and $\,\frac\pi 2\,$]
Verbalize: What is the # [number]
$\,\sin^{-1}x\,$?
It is the number (angle) between $\, -\frac{\pi}{2}\,$
and $\,\frac{\pi}{2}\,$
($\,-90^\circ$
and
$\,90^\circ\,$)
whose sine is $\,x\,.$
DOMAIN of $\,\sin^{-1}\,$: $\,[-1,1]\,$
RANGE of $\,\sin^{-1}\,$: $\,[-\frac{\pi}{2}, \frac{\pi}{2}]\,$
PROPERTIES of the ARCSINE FUNCTION
[image: partial graph of $\,y = \sin x\,$; ($1$) start with $\,x\,$ between $\,-1\,$ and $\,1\,$ on the $y$-axis; ($2$) the function $\,\sin^{-1}\,$ takes $\,x\,$ to $\,\sin^{-1}(x)\,,$ (on the $x$-axis); ($3$) the function $\,\sin\,$ takes $\,\sin^{-1} x\,$ to $\,\sin(\sin^{-1} x)\,,$ which is equal to $\,x\,$]
For all $\,x \in [-1,1]\,,$ $\,\sin(\sin^{-1}x) = x\,$
[image: graph of $\,y = \sin x\,$; ($1$) start with a value of $\,x\,$ that is NOT in the interval $\,[-\frac\pi 2,\frac\pi 2]\,$; ($2$) let $\,\sin\,$ act on $\,x\,,$ taking you to $\,\sin x\,,$ which is between $\,-1\,$ and $\,1\,$; ($3$) let $\,\sin^{-1}\,$ act on $\,\sin x\,,$ taking you to $\,\sin^{-1}(\sin x)\,,$ which is NOT equal to $\,x\,$]
For what values of $\,x\,$ is
$\,\sin^{-1}(\sin x) = x\,$?
ONLY FOR $\,x \in [-\frac{\pi}{2}, \frac{\pi}{2}]\,$!
[Mapping diagram view of prior graph]
($1$) $\,x\,$ (ANY value of $\,x\,$)
... gets mapped by the function $\,\sin\,$ to ...
($2$) $\,\sin x\,$ (always in $\,[-1,1]\,$)
... which gets mapped by the function $\,\sin^{-1}\,$ to ...
($3$) $\,\sin^{-1}(\sin x)\,$ (always in $\,[-\frac\pi 2,\frac\pi 2]\,$)

EXAMPLE
Find $\,\sin^{-1}(\sin 210^{\circ})\,$
[image:
(1) Lay off a $\,210^\circ\,$ angle
(2) Find the sine of this angle
(3) Find the angle between $\,-90^\circ\,$ and $\,90^\circ\,$ that has this sine value]
Use symmetry!
EXAMPLE
Rewrite as an algebraic expression in $\,x\,$:
$$\tan(\underbrace{\sin^{-1} x}_{:= t})$$Note: $\sin^{-1}x = \sin^{-1}\frac x1\,$ (and $\,\sin = \frac{\text{OPP}}{\text{HYP}}\,$)
[image: right triangle, with angle $\,\sin^{-1}x = t\,$ marked, OPP is $\,x\,,$ HYP is $\,1\,.$ The remaining side is calculated to be $\,\sqrt{1 - x^2}\,.$]
Then,
$$ \begin{gather} (\text{ADJ})^2 + x^2 = 1^2\cr \text{ADJ}^2 = 1 - x^2\cr \text{ADJ} = \sqrt{1 - x^2} \end{gather} $$So, for $\,x \in [-1,1]\,$ (Why?):
$$\tan(\sin^{-1} x) = \frac{x}{\sqrt{1 - x^2}}$$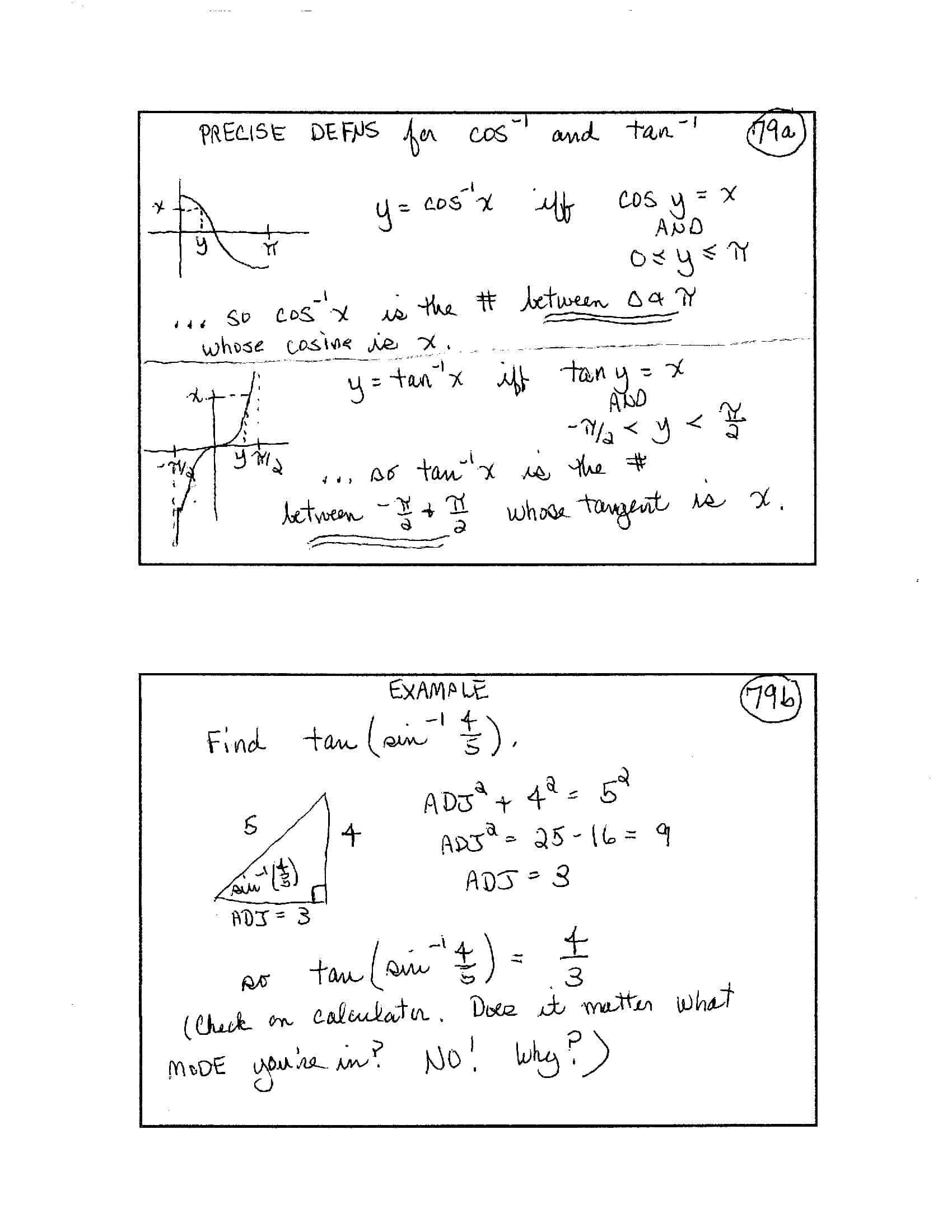
Inverse Trigonometric Function: Arccosine (Part 2)
Inverse Trigonometric Function: Arctangent (Part 1)
Inverse Trigonometric Function: Arctangent (Part 2)
PRECISE DEFNS [definitions] for $\,\cos^{-1}\,$ and $\,\tan^{-1}$
[image: graph of $\,y = \cos x\,$ on the interval $\,[0,\pi]\,,$ showing $\,x\,$ on the $y$-axis being sent (by the arccosine function) back to $\,y\,$ on the $x$-axis (between $\,0\,$ and $\,\pi\,$]
$$ \begin{gather} y = \cos^{-1}x\cr \text{iff}\cr \cos y = x\ \ \text{and}\ \ 0 \leq y \leq \pi \end{gather} $$... so $\,\cos^{-1}x\,$ is the number between $\,0\,$ and $\,\pi\,$ whose cosine is $\,x\,.$
[image: graph of $\,y = \tan x\,$ on the interval $\,(-\frac\pi 2,\frac\pi 2)\,,$ showing $\,x\,$ on the $y$-axis being sent (by the arctangent function) back to $\,y\,$ on the $x$-axis (between $\,-\frac\pi 2\,$ and $\,\frac\pi 2\,$]
$$ \begin{gather} y = \tan^{-1}x\cr \text{iff}\cr \tan y = x\ \ \text{and}\ \ -\frac\pi 2 \lt y \lt \frac\pi 2 \end{gather} $$... so $\,\tan^{-1}x\,$ is the number between $\,-\frac\pi 2\,$ and $\,\frac\pi 2\,$ whose tangent is $\,x\,.$
EXAMPLE
Find $\,\tan\left(\sin^{-1}\frac{4}{5}\right)\,.$
[image: right triangle, with angle $\,\sin^{-1}(\frac 45)\,$ labeled; it has opposite side $\,4\,$ and hypotenuse $\,5\,$; the ADJ [adjacent] side is calculated to equal $\,3\,$]
$$ \begin{gather} \text{ADJ}^2 + 4^2 = 5^2\cr \text{ADJ}^2 = 25 - 16 = 9\cr \text{ADJ} = 3 \end{gather} $$... so $\,\tan\left(\sin^{-1}\frac{4}{5}\right) = \frac{4}{3}\,.$
(Check on calculator. Does it matter what mode you’re in? NO! Why?)

SOLVING TRIGONOMETRIC EQUATIONS
Tools you’ll need:
- special $\,\Delta$s
- factoring
- zero factor law
- identities
- quadratic formula
- unit circle & RT $\,\Delta$ defns [right triangle definitions]
- periods of trig fcts [trigonometric functions]
Example: Find all real # [number] solutions: $\,\sqrt{2}\,\sin x - 1 = 0$
$$ \sin x = \frac 1{\sqrt 2} $$[images: $\,45^\circ{-}45^\circ{-}90^\circ\,$ special triangle; unit circle showing terminal points for angles with sine equal to $\,\frac 1{\sqrt 2}\,$]
In degrees:
$$ \begin{gather} x = 45^\circ \pm 360k^\circ \cr \text{or}\cr x = \underbrace{135^\circ}_{180^\circ - 45^\circ} \pm 360k^\circ\cr \text{for } k = 0,1,2,3,\ldots \end{gather} $$In radians:
$$ \begin{gather} x = \frac\pi 4 + 2\pi k \cr \text{or}\cr x = \frac{3\pi}4 + 2\pi k\cr \text{for all integers } k \end{gather} $$Example
Solve: $\;2\sin^2 x - \sin x - 1 = 0$
$$ \begin{align} \sin x &= \frac{-(-1) \pm \sqrt{1 - 4(2)(-1)}}{2(2)}\cr &= \frac{1\pm\sqrt 9}4\cr &= \frac{1\pm 3}4 \end{align} $$ $$ \sin x = 1\ \ \text{or}\ \ \sin x = -\frac{1}{2} $$[Case $1$: image showing unit circle with terminal point for $\,\sin x = 1\,.$ Recall that ‘$\,\forall\,$’ is ‘for all’ and $\,\Bbb Z\,$ is the set of integers.]
$$ \begin{gather} \sin x = 1\cr\cr x = \frac{\pi}{2} + 2\pi k \quad \forall\ k \in \mathbb{Z} \end{gather} $$[Case $2$: image showing unit circle with terminal points for $\,\sin x = -\frac12\,,$ and the $\,30^\circ{-}60^\circ{-}90^\circ\,$ special triangle]
$$ \begin{gather} \sin x = -\frac12\cr\cr x = -\frac{\pi}{6} + 2\pi k \cr \text{or}\cr x = -\frac{5\pi}{6} + 2\pi k \cr \forall\ k \in \mathbb{Z} \end{gather} $$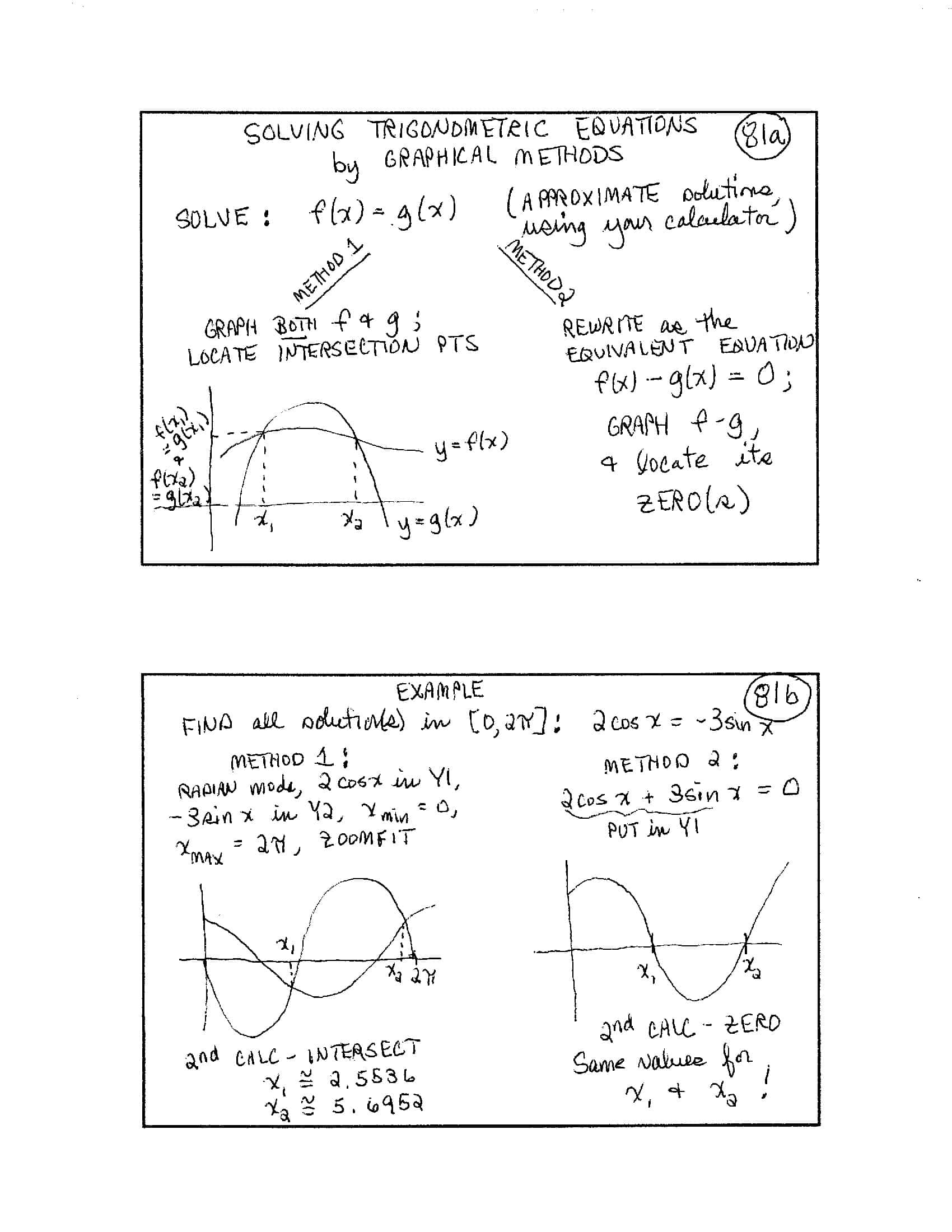
Solving Trigonometric Equations by Graphical Methods
Solve: $\,f(x) = g(x)\,$ (approximate solutions, using your calculator)
Method $1$:
Graph both $\,f\,$
and $\,g\,$;
locate intersection pts [points]
[image: graph showing sample functions $\,y = f(x)\,$ and $\,y = g(x)\,,$ with intersection points at $\,x_1\,$ and $\,x_2\,$; note that $\,f(x_1) = g(x_1)\,$ and $\,f(x_2) = g(x_2)\,$]
Method $2$:
Rewrite as the equivalent equation
$\,f(x) - g(x) = 0\,$;
graph $\,f-g\,$ and locate its zero(s)
Example
[Calculator instructions are for TI-83]
Find all solutions in $\,[0,2\pi]\,$: $\,2\cos x = -3\sin x$
Method $1$:
Radian mode, $\,2\cos x\,$ in Y$1$,
$\,-3\sin x\,$ in Y$2$, $\,x_{\min} = 0,\,x_{\max} = 2\pi\,,$
ZOOMFIT
[image: graph of both $\,y = 2\cos x\,$ and $\,y = -3\sin x\,$ on $\,[0,2\pi]\,,$ with intersection points at $\,x_1\,$ and $\,x_2\,$]
$2$nd CALC – INTERSECT:
$x_1 \approx 2.5536$
$x_2 \approx 5.6952$
Method $2$:
$\,\underbrace{2\cos x + 3\sin x}_{\text{put in Y$1$}} = 0\,$
[image: graph of $\,y = 2\cos x + 3\sin x\,,$ showing zeros at $\,x_1\,$ and $\,x_2\,$]
$2$nd CALC – ZERO
Same values for $\,x_1\,$
and $\,x_2\,$!

VECTORS
A vector has both size (length) and direction. Vectors are represented by arrows.
[image: a vector $\,\vec v = \vec{AB}\,$ starting at point $\,A\,$ (the ‘tail’) and ending at point $\,B\,$ (the ‘head’).
(When typeset, $\,\boldsymbol{v}\,$ is often bold-faced. When handwriting, put arrow over top: $\,\vec{v}\,$)
$A\,$ is the initial point.
$B\,$ is the terminal point.
$\|\vec{AB}\|\,$ denotes the length (or magnitude) of $\,\vec{AB}\,$; note that $\,\|\vec{AB}\| \ge 0\,.$
Uses for vectors: to denote velocity, forces, $\ldots$
Working with the Arrow Representation for Vectors
Two vectors are equal when they have the same magnitude and direction. (It doesn’t matter where they ‘start’.)
Multiplying a vector by a scalar (a number): $\,\vec u\,,$ $\,\frac{1}{2}\vec{u}\,,$ $\,2\vec{u}\,,$ $-\vec{u}\,,$ $\,-2\vec{u}$
Addition of vectors: ‘head-to-tail’ [attach the head of $\,\vec{u}\,$ to the tail of $\,\vec{v}\,$ to get $\,\vec{u} + \vec{v}\,$]
$\vec{u} - \vec{v} = \vec{u} + (-\vec{v})$

Analytic Representation for Vectors
$\vec{v} = \langle a, b \rangle$ (use angle brackets)
- $a =$ horizontal component of $\,\vec{v}\,$ (to RIGHT, positive; to LEFT, negative)
- $b =$ vertical component of $\,\vec{v}\,$ (UP, positive; DOWN, negative)
EX [examples]
$\langle 1, 2 \rangle \quad \langle 2, 1 \rangle \quad \langle -1, 2 \rangle \quad \langle 0, 2 \rangle$
Working with the Analytic Representation
Multiplying a vector by a scalar:
Let $\,k \in \mathbb{R}\,,$ $\,\vec{v} = \langle a, b \rangle\,.$
Then:
Example:
$$ \begin{align} \vec{v} &= \langle -1, 3 \rangle\cr\cr 2 \vec{v} &= \langle -2, 6 \rangle\cr\cr -\vec{v} &= \langle 1, -3 \rangle \end{align} $$Adding / Subtracting Vectors:
$$ \vec{u} = \langle u_1, u_2 \rangle\,, \quad \vec{v} = \langle v_1, v_2 \rangle $$ $$ \begin{align} \vec{u} + \vec{v} &= \langle u_1 + v_1\,,\, u_2 + v_2 \rangle\cr\cr \vec{u} - \vec{v} &= \langle u_1 - v_1\,,\, u_2 - v_2 \rangle \end{align} $$
Unit (length $\,1\,$) Vectors
$$ \begin{gather} \hat\imath := \langle 1, 0 \rangle\cr\cr \hat\jmath := \langle 0, 1 \rangle \end{gather} $$(When typeset, $\,\boldsymbol{i}\,$ and $\,\boldsymbol{j}\,$ are bold; when handwriting, use ‘hat’.)
Note: Every vector can be expressed in terms of $\,\hat\imath\,$ and $\,\hat\jmath\,$:
$$ \begin{align} \langle a, b \rangle &= \langle a, 0 \rangle + \langle 0, b \rangle\cr\cr &= a \langle 1, 0 \rangle + b \langle 0, 1 \rangle\cr\cr &= a \hat\imath + b \hat\jmath \end{align} $$Formula for Length of a Vector
Let $\,\vec{v} = \langle a, b \rangle$.
Then,
$\,\|\vec{v}\| = \sqrt{a^{2} + b^{2}}\,.$
Also, for $\,k \in \mathbb{R}\,,$
$$ \begin{align} \|k \vec{v}\| &= \|\langle ka, kb \rangle\|\cr\cr &= \sqrt{(ka)^{2} + (kb)^{2}}\cr\cr &= \sqrt{k^{2} (a^{2} + b^{2})}\cr\cr &= \sqrt{k^{2}} \, \sqrt{a^{2} + b^{2}}\cr\cr &= |k| \cdot \|\vec{v}\| \end{align} $$So: $\,\|k \vec{v}\| = |k| \cdot \|\vec{v}\|\,$
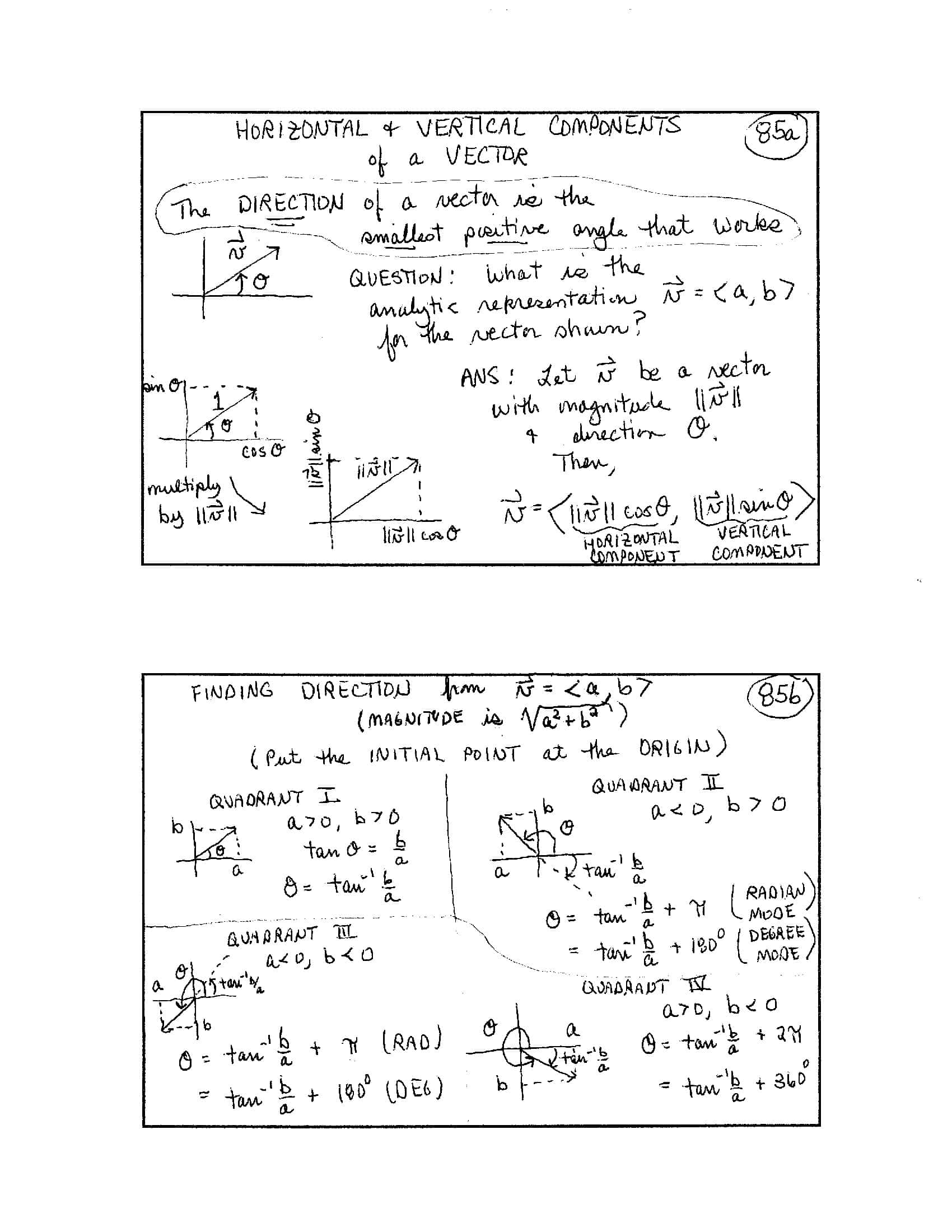
Vectors: From Horizontal/Vertical Components to Direction/Magnitude
Horizontal & Vertical Components of a Vector
The DIRECTION of a vector is the smallest positive angle that works.
[image: a vector $\,\vec v\,$ with direction $\,\theta\,$]
QUESTION: What is the analytic representation $\,\vec{v} = \langle a,b \rangle\,$ for the vector shown?
[images: vector with length $\,1\,$ and direction $\,\theta\,,$ tail at origin, head has coordinates $\,(\cos\theta,\sin\theta)\,$; multiply length of vector by $\,\|\vec v\|\,$ to give desired vector with analytic representation $\,(\|\vec v\|\cos\theta,\|\vec v\|\sin\theta)\,$]
ANS [answer]: Let $\,\vec{v}\,$ be a vector with magnitude $\,\|\vec{v}\|\,$ and direction $\,\theta\,.$ Then:
$$ \vec{v} = \langle\, \underbrace{\|\vec{v}\|\cos\theta}_{\substack{\text{horizontal}\\ \text{component}}}\,,\, \underbrace{\|\vec{v}\|\sin\theta}_{\substack{\text{vertical}\\ \text{component}}} \rangle $$Finding Direction from $\,\vec{v} = \langle a,b \rangle\,$
(Magnitude is $\,\sqrt{a^2+b^2}\,$)
(Put the initial point at the origin.)
Quadrant I:
$a\gt 0,\ b\gt0\,$
$\tan\theta = \frac ba$
$\theta = \tan^{-1}(\frac{b}{a})$
Quadrant II:
$a\lt 0,\ b\gt 0\,$
$\theta = \tan^{-1}(\frac ba) + \pi \,$ (radian mode)
$\theta = \tan^{-1}(\frac ba) + 180^\circ \,$ (degree mode)
Quadrant III:
$a\lt 0,\ b\lt 0\,$
$\theta = \tan^{-1}(\frac ba) + \pi \,$ (rad)
$\theta = \tan^{-1}(\frac ba) + 180^\circ$ (deg)
Quadrant IV:
$a\gt 0,\ b\lt 0\,$
$\theta=\tan^{-1}(\frac ba) + 2\pi \,$
$\theta=\tan^{-1}(\frac ba) + 360^\circ$

BEARING; VELOCITY VECTORS
[image: correct directions for North, South, West, East]
Memory devices:
- ‘W E’ versus ‘E W’!!
-
As you go thru the day $\,\circlearrowright\,$
Never Eat Soggy Waffles!
A bearing is an acute angle measured from due North or due South.
Examples:
N $30^\circ$ E [head North; lean $\,30^\circ\,$ East]
N $30^\circ$ W [head North; lean $\,30^\circ\,$ West]
S $30^\circ$ E [head South; lean $\,30^\circ\,$ East]
S $30^\circ$ W [head South; lean $\,30^\circ\,$ West]
Velocity is a vector quantity; it has both speed (the length of the vector) and direction.
EXAMPLE: TRUE SPEED & DIRECTION
A jet flies thru wind that is blowing at $55$ miles/hour (mph) in the direction N $30^\circ$ E. The jet goes $765$ mph in still air. The pilot heads the jet in the direction N $45^\circ$ E.
Find the true velocity of the jet as a vector:
(Sketches not to scale)
Wind:
$$ \begin{align} \vec{W} &= \langle 55 \cos 60^\circ\,,\, 55 \sin 60^\circ \rangle\cr &= \langle \frac{55}2\,,\, \frac{55\sqrt 3}{2} \rangle \end{align} $$Jet:
$$ \begin{align} \vec{J} &= \langle 765 \cos 45^\circ\,,\, 765 \sin 45^\circ \rangle\cr &= \langle \frac{765}{\sqrt{2}}\,,\, \frac{765}{\sqrt{2}} \rangle \end{align} $$True Velocity of Jet:
$$ \begin{align} \vec{W} + \vec{J} &= \langle \frac{55}2 + \frac{765}{\sqrt 2}\,,\, \frac{55\sqrt 3}2 + \frac{765}{\sqrt 2} \rangle\cr &\approx \langle 568.44\,,\, 588.57 \rangle \end{align} $$True Speed of Jet:
$$ \|\text{true velocity}\| \approx 818.25 \, \text{mph} $$True Direction of Jet equals direction of true velocity:
$$ \begin{gather} \tan^{-1} \left(\frac{588.57}{568.44}\right) \approx 46.00^\circ\cr\cr 90^\circ - 46^\circ = 44^\circ\cr\cr \text{As a bearing:}\ \ \text{N}\, 44^\circ\, \text{E} \end{gather} $$
Forces Acting on an Object
A free-body diagram shows all the forces acting on an object.
[image: an FBD (free-body diagram) with forces $\,\vec F_1\,,$ $\,\vec F_2\,$ and $\,\vec F_3\,$]
An object is in equilibrium if the sum of the forces acting on the object is $\,\vec{0}\,$ (the zero vector).
[image: a right triangle with hypotenuse $\,H\,$ and angle $\,\theta\,$; the side adjacent to the labeled angle has length $\,H\cos\theta\,$ and the side opposite has length $\,H\sin\theta\,$]
Example
[image: an object in equilibrium, with a weight of $\,2000\,$ lbs [pounds] and cables at angles $\,22.3^\circ\,$ and $\,41.5^\circ\,$]
Find $\,\vec{T}_1\,$ and $\,\vec{T}_2\,$ (the tensions in the cables).
Let $\,T_1\,$ and $\,T_2\,$ denote the lengths of $\,\vec{T}_1\,$ and $\,\vec{T}_2\,$. Then:
$$ \begin{gather} T_1\cos 22.3^\circ = T_2\cos 41.5^\circ\cr \text{and}\cr 2000 = T_1\sin 22.3^\circ + T_2\sin 41.5^\circ \end{gather} $$Solving for $\,T_1\,$ and $\,T_2\,$ gives:
$$ \begin{gather} T_1 \approx 1669.43\cr \text{and}\cr T_2 \approx 2062.30 \end{gather} $$Thus:
$$ \begin{align} \vec{T}_1 &= \langle -T_1\cos 22.3^\circ\,,\, T_1\sin 22.3^\circ \rangle\cr &\approx \langle -1544.1\,,\, 633.5 \rangle\cr \text{and}\cr \vec{T}_2 &= \langle T_2\cos 41.5^\circ\,,\, T_2\sin 41.5^\circ \rangle\cr &\approx \langle 1544.6\,,\, 1366.5 \rangle \end{align} $$
Introduction to Partial Fraction Expansion/Decomposition (PFE) (Part 2)
Partial Fraction Decomposition (Expansion)
You already know how to add fractions:
$$ \begin{align} &\frac{1}{x-1} + \frac{1}{2x+1}\cr\cr &\quad = \frac{(2x+1) + (x-1)}{(x-1)(2x+1)}\cr\cr &\quad = \frac{3x}{2x^2 - x - 1} \end{align} $$
The process of going backwards: from
$\,
\frac{3x}{2x^2 - x - 1}
\,$
back to
$\,
\frac{1}{x-1} + \frac{1}{2x+1}
\,$
is called
Partial Fraction Decomposition/
Review
$$ \begin{gather} ax^2 + bx + c \ \ (a\ne 0)\ \ \text{is irreducible}\cr\cr \text{iff}\ \ \text{[if and only if]}\cr\cr \underbrace{b^2 - 4ac}_{\text{the discriminant}} \lt 0 \end{gather} $$Every polynomial with real # [number] coefficients can be factored into linear factors and irreducible quadratics.
EX [Example]:
$\,x^2 + x + 2\,$
is irreducible since its discriminant is negative:

Different Linear Factors
Find the PFE [Partial Fraction Expansion] of $\,\displaystyle\frac{x+6}{x^2+3x}\,.$
(Degree of numerator must be $\,\lt\,$ degree of denominator;
if not, do a long division)
Step $1$: Completely factor denominator:
$$x^2+3x = x(x+3)$$Step $2$: Each distinct linear factor $\,ax+b\,$ gives rise to a term of the form $\,\frac{A}{ax+b}\,$ in the PFE:
$$ \begin{align} \frac{x+6}{x^2+3x} &= \frac{x+6}{x(x+3)}\cr\cr &= \frac{A}{x} + \frac{B}{x+3} \end{align} $$... (continued)
Step $3$: Solve for the unknown constants:
Clear fractions:
$$ \underbrace{x+6 = A(x+3)+Bx}_{\text{must be true for all values of $\,x\ $}} $$When $\,x=-3\,$:
$$ \begin{gather} -3+6=A(-3 + 3)+B(-3)\cr\cr 3=-3B\cr\cr B=-1 \end{gather} $$When $\,x=0\,:$
$$ \begin{gather} 0+6=A(0+3)+B(0)\cr\cr 6=3A\cr\cr A=2 \end{gather} $$So:
$$ \frac{x+6}{x^2+3x} = \frac{2}{x} - \frac{1}{x+3} $$Step $4$: Spot check:
When $\,x\overset{\text{say}}{=} 1\,$:
$$ \begin{gather} \frac{1+6}{1^2+3(1)} \overset{?}{=} \frac{2}{1} - \frac{1}{1+3} \cr\cr \frac74 = \frac74\ \ \unicode{x263A} \end{gather} $$
Repeated Linear Factors
A factor of $\,(ax+b)^n\,$ in denominator gives rise to $\,n\,$ terms in the PFE:
$$ \frac{A_1}{ax+b} + \frac{A_2}{(ax+b)^2} + \cdots + \frac{A_n}{(ax+b)^n} $$EX [Example]: Find PFE of $\,\frac{3x^2+15x+8}{(x+1)^2(x-3)}$
$$ \frac{3x^2+15x+8}{(x+1)^2(x-3)} = \frac{A}{x-3} + \frac{B}{x+1} + \frac{C}{(x+1)^2} $$ $$ 3x^2+15x+8 = A(x+1)^2 + B(x+1)(x-3) + C(x-3) $$(... continued)
$x=-1$:
$$ \begin{gather} 3 - 15 + 8 = C(-4)\cr -4 = -4C\cr C=1 \end{gather} $$$x=3$:
$$ \begin{gather} 27 + 45 + 8 = 16A\cr 80 = 16A\cr A=5 \end{gather} $$Equate coefficients to find $\,B\,$:
$x^2$:
$$ \begin{gather} 3 = A+B\cr 3 = 5 + B\cr B=-2 \end{gather} $$OR $\,x\,$ (hard)
OR CONSTANT:
$$ \begin{gather} 8 = A - 3B - 3C\cr 8 = 5 - 3B - 3\cr 6 = -3B\cr B=-2 \end{gather} $$So:
$$ \frac{3x^2+15x+8}{(x+1)^2(x-3)} = \frac{5}{x-3} - \frac{2}{x+1} + \frac{1}{(x+1)^2} $$Spot check (set $\,x=0\,$):
$$ \begin{gather} \frac{8}{(1)(-3)} \stackrel{?}{=} \frac{5}{-3} - \frac{2}{1} + 1\cr \text{😊} \end{gather} $$
IRREDUCIBLE QUADRATIC FACTORS
A factor of $\, (a x^2 + b x + c)^n \,$ ($\, b^2 - 4ac \lt 0 \,$) in the denominator gives rise to $\, n \,$ terms in the PFE [Partial Fraction Expansion]:
$$ \begin{align} &\frac{A_1 x + B_1}{a x^2 + b x + c} + \frac{A_2 x + B_2}{(a x^2 + b x + c)^2}\cr\cr &\quad + \cdots + \frac{A_n x + B_n}{(a x^2 + b x + c)^n} \end{align} $$EXAMPLE
Write FORM of PFE [Partial Fraction Expansion]. Do not solve for the unknown constants:
$$ \begin{align} &\frac{7x^3 - 5x + 4}{(x^2 + 3)^2 (x - 1)^3 \,x\, (2x - 3)}\cr\cr &\quad = \frac{A_1 x + B_1}{x^2 + 3} + \frac{A_2 x + B_2}{(x^2 + 3)^2}\cr\cr &\qquad + \frac{C_1}{x - 1} + \dfrac{C_2}{(x - 1)^2} + \dfrac{C_3}{(x - 1)^3}\cr\cr &\qquad + \frac{D}{x} + \frac{E}{2x - 3} \end{align} $$
Identifying Conics by the Discriminant (Part 1)
Identifying Conics by the Discriminant (Part 2)
Conic Sections
FACT: Every equation of the form
$$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$graphs as a conic (or degenerate conic). Conics are curves formed by the intersection of a plane with a pair of circular cones.
[images: circle, ellipse, parabola, hyperbola]
Identifying Conics by the Discriminant
The expression $\,B^2 - 4AC\,$ is called the discriminant of the equation $\,Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0\,.$
- $B^2 - 4AC = 0$ PARABOLA (possibly degenerate)
- $B^2 - 4AC \lt 0$ ELLIPSE (possibly degenerate; special case is a CIRCLE)
- $B^2 - 4AC \gt 0$ HYPERBOLA (possibly degenerate)
EX [Example]
$$ \begin{gather} y = x^2 - 5x + 1\cr x^2 - 5x - y + 1 = 0\cr A = 1,\ \ B = 0,\ \ C = 0\cr B^2 - 4AC = 0\cr \text{Parabola} \end{gather} $$EX [Example]
$$ \begin{gather} x^2 + y^2 = 0\cr A = 1,\ \ B = 0,\ \ C = 1\cr B^2 - 4AC = -4\cr \text{Ellipse} \end{gather} $$(This is a degenerate circle, centered at $\,(0,0)\,$ with radius $\,0\,,$ a ‘point circle.’)

Parabolas
Geometric Definition: A parabola is the set of points in a plane that are equidistant from a fixed point (called the focus) and a fixed line (called the directrix).
[image: a parabola with given focus and directrix, also showing the vertex, axis of parabola, and two additional points on the parabola]
Three points are easy to get!
[image:
($1$) The vertex is halfway between the focus and directrix;
($2$) and ($3$) Sweep the radius (from focus to directrix) $\,90^\circ\,$ in both directions]
The focus is always ‘inside’ the parabola.
Parabolas as Reflectors/Collectors
Reflector:
Light emitted from the focus
is reflected parallel to the axis!
(Think Hollywood beams of light!!)
Collector:
Light coming in parallel to the axis
is ‘collected’ (focused) at the focus.

Parabolas: Vertex at the origin, Directrix parallel to the $\,x\,$ or $\,y$-axis
[image: parabola opening up, with vertex at the origin, focus $\,F(0,p)\,,$ directrix $\,y = -p\,,$ and typical point $\,P(x,y)\,$]
We seek pts [points] $\,P(x, y)\,$ such that:
$$ \begin{align} &\text{distance from $\,P\,$ to $\,F\,$}\cr &\quad = \text{distance from $\,P\,$ to directrix} \end{align} $$ $$ \sqrt{(x - 0)^2 + (y - p)^2} = y - (-p) $$Square both sides:
$$ \begin{gather} x^2 + (y - p)^2 = (y + p)^2\cr\cr x^2 + \cancel{y^2} - 2py + \cancel{p^2} = \cancel{y^2} + 2py + \cancel{p^2}\cr\cr x^2 = 4py \end{gather} $$
Key idea: coefficient of $\,y\,$ is $\,4p\,.$
$|p| =\,$ distance from origin to focus
[image: parabola opening right, with vertex at the origin, focus $\,F(p,0)\,,$ directrix $\,x = -p\,$]
Similarly, $y^2 = 4px$ [for a parabola opening right or left]
Sketching Parabolas
[images:
parabola opening up, $\,y\ge 0$
parabola opening down, $\,y\le 0$
parabola opening right, $\,x\ge 0$
parabola opening left, $\,x\le 0\,$]
Don’t memorize lots of stuff! Let the equations tell you the shape!
EX [Example]: Sketch the graph of $\,8x^2 + 12y = 0$
SOLN [Solution]:
The discriminant $\,= 0\,$; it's a parabola.
Isolate the squared term:
[image: parabola opening down, focus on $y$-axis at $\,-\frac 38\,,$ directrix $\,y = \frac 38\,$]

Finding the Equation of a Parabola (with vertex at the origin and a given focus)
$F(0,2)\,$ (so directrix is $\,y = -2\,$)
Safest approach—use the definition!
[image: parabola with vertex at the origin, focus $\,F(0,2)\,,$ directrix $\,y = -2\,$ and typical point $\,(x,y)\,$ on the parabola]
$$ \begin{gather} \sqrt{(y - 2)^2 + (x - 0)^2} = y - (-2)\cr\cr (y - 2)^2 + x^2 = (y + 2)^2\cr\cr \cancel{y^2} - 4y + \cancel{4} + x^2 = \cancel{y^2} + 4y + \cancel{4}\cr\cr x^2 = 8y \end{gather} $$Alternative Approach (use known shape)
[images: parabolas opening up and down, with standard forms $\,x^2 = 4py\,$; parabolas opening left and right, with standard forms $\,y^2 = 4px\,$]
$$ \begin{gather} \underbrace{x^2}_{\ge 0} = 4py\cr \text{($\,p\,$ is $y$-value of focus)}\cr p = 2\cr \text{so}\cr x^2 = 4\cdot 2y\cr x^2 = 8y \end{gather} $$ $$ \underbrace{y^2}_{\ge 0} \ \ \ = \underbrace{4px}_{\text{so this must be $\,\ge\, 0\,$;}} $$thus all $x$-values have the same sign.
Example
Find equation of parabola with vertex at the origin, directrix parallel to $y$-axis, passing through pt [point] $\,(1,3)\,.$
[image: parabola with vertex at origin, point $\,(1,3)\,$ on parabola, general location of directrix dashed in]
SOLN [solution]: must open to right, so $x$-values are all $\,\ge 0\,$:
FORM of equation: $\,y^2 = 4px$
$(1,3)\,$ on parabola: $\,3^2 = 4p(1)$
$$ \begin{gather} 9 = 4p\cr p = \frac 94\cr \text{so}\cr y^2 = 4(\frac 94)x\cr y^2 = 9x \end{gather} $$and focus is $\,F(0,\frac 94)\,.$

Reflecting Property of an Ellipse (Part 1)
Reflecting Property of an Ellipse (Part 2)
Ellipse
Geometric Definition: An ellipse is determined by two fixed points (called the foci, plural of focus) and a positive number $\,k\,.$ It is the set of all points $\,P\,$ such that
$$ \underbrace{d(P,F_1) + d(P,F_2)}_{\text{the SUM of the distances to the two foci ...}} = \underbrace{k}_{\text{... is constant}} $$Note:
$$ k \overbrace{\gt}^{\text{must be}} \text{distance from $\,F_1\,$ to $\,F_2$} $$[image: an ellipse, showing major axis, minor axis, and foci $\,F_1\,$ and $\,F_2\,$]
Reflecting Property of Ellipses
[image: ellipse with two foci, showing a ray emanating from one focus, hitting the ellipse, and being reflected through the other focus]
Light emitted from one focus will be reflected through the other focus!

Ellipse—Center at the Origin
Let:
- $c =\,$ distance from center to each focus
- $a =\,$ distance from center to MAJOR AXIS intercept
Note: $\,a\gt c\,$ so $\,a^2\gt c^2$
[image: ellipse with foci on the $x$-axis at $\,c\,$ and $\,-c\,,$ major axis intercept at $\,a\,,$ and minor axis intercept at $\,b\,$]
NOTE: The constant for this ellipse is:
$$ (a-c) + (a-(-c)) = 2a $$Let $\,(x, y)\,$ be a pt [point] on the ellipse. Then:
$$\sqrt{(x - (-c)^2 + (y-0)^2} + \sqrt{(x - c)^2 + (y-0)^2} = 2a$$(Isolate a square, square both sides, repeat ...)
$$ \begin{gather} (\underbrace{a^2 - c^2}_{:= b^2})x^2 + a^2y^2 = a^2(\underbrace{a^2 - c^2}_{:= b^2})\cr \text{(divide by $a^2b^2$)}\cr\cr \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \end{gather} $$LARGER # [number] is under MAJOR AXIS variable.
$a^2 - c^2 = b^2\,,$ so $\,a^2 \gt b^2\,$ so $\,a \gt b$
Graphing an Ellipse
EX [Example]: Graph $\,4x^2 + 25y^2 = 100\,$; find foci.
(Discriminant is $\,0^2 - 4(4)(25) \lt 0\,$; an ellipse)
- Get ‘$\,1\,$’ on RHS [right-hand side]: $$\frac{x^2}{25} + \frac{y^2}{4} = 1$$ ($\,25\,$ is larger #; $\,x\,$ is major axis)
- Identify major axis, sketch easy pts [points] $$ \begin{gather} x = 0:\ \ y = \pm 2\cr y = 0:\ \ x = \pm 5 \end{gather} $$
[image: ellipse with easy points shown; since the sum of the distances from the point $\,(0,2)\,$ to each focus must equal $\,10\,,$ the hypotenuse of the triangle shown must be $\,5\,$]
$$ \begin{gather} 2^2 + c^2 = 5^2\cr c^2 = 25 - 4 = 21\cr c = \sqrt{21} \end{gather} $$
Summary: Equations of Ellipses in Standard Form
Finding the Equation of an Ellipse
EX [Example]: Find the equation of the ellipse with center at the origin, focus $\,(0, 3)\,,$ and crossing the $y$-axis at $\,4\,.$
[image: ellipse showing foci $\,(0,3)\,$ and $\,(0,-3)\,,$ major-axis intercepts $\,4,\,-4\,,$ minor-axis intercept at $\,b\,$]
Method $1$: Use the definition! (long...)
Method $2$: Use knowledge of standard forms: $\,a = 4\,,$ $\,c = 3$
$$ \begin{gather} \frac{y^2}{a^2} + \frac{x^2}{b^2} = 1\cr\cr b^2 + 3^2 = 4^2\cr b^2 = 16 - 9 = 7\cr b = \sqrt{7}\cr\cr \text{so}\cr \frac{y^2}{16} + \frac{x^2}7 = 1 \end{gather} $$Finding the Equation of an Ellipse
... with length of major axis $\,6\,$ (distance between major axis intercepts), center at origin, length of minor axis $\,2\,,$ foci on $x$-axis.
[image: ellipse with center at origin, focus $\,(c,0)\,,$ major axis intercept $\,(3,0)\,,$ minor axis intercept $\,(0,1)\,$]
$$ \begin{gather} \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\cr\cr a = 3\,,\ b = 1\cr\cr \text{so}\cr \frac{x^2}9 + y^2 = 1 \end{gather} $$NOTE:
$$ \begin{gather} c^2 + 1^2 = 3^2\cr c^2 = 8\cr c = \sqrt{8} \approx 2.83 \end{gather} $$
Equations of Hyperbolas in Standard Form (Part 1)
Equations of Hyperbolas in Standard Form (Part 2)
Graphing Hyperbolas (Part 1)
Graphing Hyperbolas (Part 2)
Reflecting Property of a Hyperbola (Part 1)
Reflecting Property of a Hyperbola (Part 2)
Hyperbolas
[image: a hyperbola with foci $\,F_1\,$ and $\,F_2\,,$ showing the vertices and a point $\,P\,$ on the hyperbola with its distances to the two foci]
A hyperbola is the set of points in a plane, with the property that the difference of the distances from two fixed points (the foci) is constant.
$$d(P, F_1) - d(P, F_2) = \text{constant}$$
Reflecting property: Light aimed at one focus is reflected toward the other focus.
[image: hyperbola, showing light aimed toward $\,F_1\,,$ hitting the hyperbola and being reflected toward $\,F_2\,$]
Graphing a Hyperbola
[image: hyperbola with foci on $x$-axis, vertices at $\,a\,$ and $\,-a\,,$ a box through vertices and through $\,b\,$ and $\,-b\,$ on $y$-axis, diagonals of box sketched in]
Derivation shows that:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$EX [Example]: Graph $\,9x^2 - 4y^2 = 36\,$
Discriminant:
$$ \begin{align} B^2 - 4AC &= 0^2 - 4(9)(-4)\cr &\gt 0\,, \text{so HYP [hyperbola]} \end{align} $$($1$) Get ‘$1$’ on RHS [Right-Hand Side]:
$$ \begin{gather} \frac{9x^2}{36} - \frac{4y^2}{36} = \frac{36}{36}\cr\cr \frac{x^2}{4} - \frac{y^2}{9} = 1 \end{gather} $$($2$) Find intercepts: the equation tells you which axis the foci lie on:
$$y = 0:\ \ x = \pm 2$$($3$) Also plot $\,\pm b\,$ ($\,b^2 = 9\,$) on other axis; sketch in box and diagonals of box
($4$) Sketch in the hyperbola!
[image: hyperbola with vertices at $\,2\,$ and $\,-2\,$ on the $x$-axis, showing box with corners $\,(\pm 2,\pm 3)\,$ and the diagonals of the box; the hyperbola approaches these diagonals as $\,x\,$ goes to $\,\pm\infty\,$]

Shifted Conics
Recall (for $\,k \gt 0\,$):
| replacing every | $\,x\,$ | by | $\,x + k\,$ | shifts | LEFT | $\,k\,$ |
| $\,x\,$ | by | $\,x - k\,$ | RIGHT | $\,k\,$ | ||
| replacing every | $\,y\,$ | by | $\,y + k\,$ | shifts | DOWN | $\,k\,$ |
| $\,y\,$ | by | $\,y - k\,$ | UP | $\,k\,$ |
(All counter-intuitive!)
Note:
$$ \begin{gather} y = f(x)\cr \color{blue}{\text{(add $\,3\,$ to previous $y$-values; UP $\,3$)}}\cr \color{red}{y = f(x) + 3} \end{gather} $$versus
$$ \begin{gather} y = f(x)\cr \color{blue}{\text{(replace $\,y\,$ by $\,y-3\,,$ UP $\,3$)}}\cr y - 3 = f(x)\cr \color{red}{y = f(x) + 3} \end{gather} $$Different thought processes—same result!
Example
Graph: $\,x^2 + 6x + 16y + 9 = 0$
Discriminant:
$$ \begin{align} B^2 - 4AC &= 0^2 - 4(1)(0)\cr &= 0\ \ \text{(parabola)} \end{align} $$Complete square:
$$ \begin{gather} x^2 + 6x\ \underline{+\ 9} = -16y - 9 \ \underline{+\ 9}\cr (x + 3)^2 = -16y \end{gather} $$FIRST graph the ‘basic model’ $\,x^2 = -16y\,$ ($\,x^2\ge 0\,,$ so $\,-16y\ge 0\,,$ so $\,y\le 0\,$; $\,4p = -16\,$ so $\,p = -4\,$)
[image: a parabola, opening down, with focus at $\,-4\,$]
Then replace $\,x\,$ by $\,x + 3\,,$ shifts LEFT $\,3\,$:
$$(x + 3)^2 = -16y $$$y$-int [intercept] (set $\,x = 0\,$):
$$ \begin{gather} 3^2 = -16y\cr y = -\frac 9{16} \end{gather} $$[image: parabola with vertex at $\,(-3,0)\,$ and focus at $\,(-3,-4)\,,$ crosses $y$-axis at $\,-\frac 9{16}\,$]
Is $\,(-3,0)\,$ on graph?
$$ \begin{gather} (-3+3)^2 \overset{?}{=} -16(0)\cr \text{Yes!!} \end{gather} $$