Finding Vertical Asymptotes

You can't divide by zero. But, as you divide by numbers closer and closer to zero, the outputs blow up. They get bigger and bigger, without bound.

Suppose a ladder is leaning against a wall, and you're working at the top of the ladder. Someone (mischievous!) starts pulling the bottom of the ladder away at a constant rate. The top of the ladder slides down the wall, with you on it. You'll drop faster and faster as you near the ground! (Interested? Search for the ‘falling ladder problem’. Don't try this!)

Model these scenarios using mathematics, and you'll find yourself dealing with vertical asymptotes.

As introduced in the earlier section, Introduction to Asymptotes:

In particular, here is the definition of a vertical asymptote:

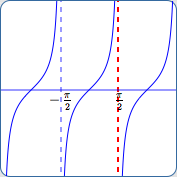
The tangent function has infinitely many vertical asymptotes.

For example, the vertical line $\,x = \frac{\pi}{2}\,$ is a vertical asymptote:

• as $\,x\rightarrow {\frac{\pi}{2}}^{+}\,,$ $\,\tan x\rightarrow -\infty\,$
• as $\,x\rightarrow {\frac{\pi}{2}}^{-}\,,$ $\,\tan x\rightarrow \infty\,$

Notes About Vertical Asymptotes

Outputs ‘Blow Up’ Near Vertical Asymptotes

Roughly, outputs ‘blow up’ near a vertical asymptote! They get very big and positive (go to $\,+\infty\,$), or very big and negative (go to $\,-\infty\,$).

(A ‘big’ number is far from zero—it can be to the right or left of zero.)

Typically, the closer the inputs to the value of $\,x\,$ where the vertical asymptote occurs, the bigger the outputs.

How To Read Aloud ‘$\ x\rightarrow c^+\ $’ and ‘$\ x\rightarrow c^-\ $’

The sentence ‘$\,x\rightarrow c^+\,$’ is read aloud as ‘$\,x\,$ approaches $\,c\,$ from the right’.

This is made precise in Calculus, but roughly means that $\,x\,$ is greater than $\,c\,$ and getting as close to $\,c\,$ as desired from this right-hand side.

Similarly, ‘$\,x\rightarrow c^-\,$’ is read aloud as ‘$\,x\,$ approaches $\,c\,$ from the left’.

Roughly, this means that $\,x\,$ is less than $\,c\,$ and getting as close to $\,c\,$ as desired from this left-hand side.

All These Graphs Have Vertical Asymptote $\,\color{red}{x = 2}$

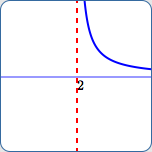
As $\,x\rightarrow 2^+\,,$ $\,y \rightarrow \infty$

As $\,x\,$ approaches $\,2\,$ from the right, $\,y\,$ goes to infinity

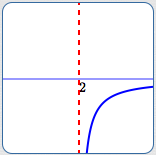
As $\,x\rightarrow 2^+\,,$ $\,y \rightarrow -\infty$

As $\,x\,$ approaches $\,2\,$ from the right, $\,y\,$ goes to negative infinity

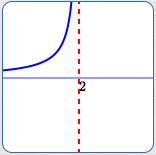
As $\,x\rightarrow 2^-\,,$ $\,y \rightarrow \infty$

As $\,x\,$ approaches $\,2\,$ from the left, $\,y\,$ goes to infinity

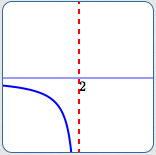
As $\,x\rightarrow 2^-\,,$ $\,y \rightarrow -\infty$

As $\,x\,$ approaches $\,2\,$ from the left, $\,y\,$ goes to negative infinity

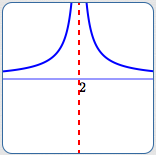
As $\,x\rightarrow 2^+\,,$ $\,y \rightarrow \infty$

As $\,x\rightarrow 2^-\,,$ $\,y \rightarrow \infty$

Vertical Asymptotes for Rational Functions

How can a rational function (a ratio of polynomials) ‘blow up’ near a finite input? When you're ‘trying’ to divide by zero! Remember—dividing by a very small number gives a very big number.

A Rational Function Might Not Have Any Vertical Asymptotes

For example, $\,\displaystyle f(x) = \frac{1}{x^2 + 1}\,$ has no vertical asymptotes, because the denominator is never zero.

The Condition $\,N(c)\ne 0\,$ Is Important

If $\,N(c) = 0\,$ (as in the following two examples), you could have either a vertical asymptote or a hole at $\,c\,$:

• The function $\displaystyle\,\frac{x-2}{(x-2)^2}\,$ has a vertical asymptote at $\,2\,.$ Why? $$\cssId{s64}{\frac{x-2}{(x-2)^2} = \frac{1}{x-2}}$$ In this case, there are more factors of $\,x-2\,$ in the denominator than in the numerator.
• The function $\displaystyle\,\frac{(x-2)^2}{x-2}\,$ has a hole at $\,2\,.$ Why? For $\,x\ne 2\,,$ $$\cssId{s68}{\frac{(x-2)^2}{x-2} = x-2}$$ In this case, there are more factors of $\,x-2\,$ in the numerator than in the denominator.

Checking the Behavior of a Rational Function Near a Vertical Asymptote

Given a vertical asymptote, you usually want to know how the function behaves nearby. Are the outputs going to infinity? To negative infinity?

Although you could certainly use a graphing calculator or WolframAlpha to see this behavior, you should also be able to determine it algebraically, as shown next.

Example

The function $\displaystyle\,f(x) = \frac{-3}{2x + 1}\,$ has a vertical asymptote at $\,x = -\frac 12\,.$

Why?   The denominator, $\,2x + 1\,,$ is zero when $\,x = -\frac 12\,,$ and the numerator is (always) nonzero.

Here is the thought process for determining what the outputs from $\,f\,$ look like, close to $\,-\frac 12\,$:

Consider values of $\,x\,$ a bit less than $\,-\frac 12\,$ (i.e., just to the left of $\,-\frac 12\,$):

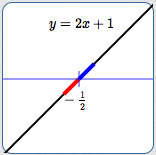
• The denominator is small and negative (see the graph of $\,y = 2x+1\,$ below)
• The numerator is negative

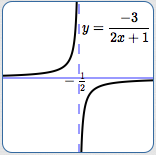
Thus:

Observe that the notation  $\,\frac{(-)}{(\text{small }-)}\,$   is being used to denote a (normal-sized) negative number, divided by a small negative number—which produces a large positive number.

Next, consider values of $\,x\,$ a bit more than $\,-\frac 12\,$ (i.e., just to the right of $\,-\frac 12\,$):

• The denominator is small and positive (see the graph of $\,y = 2x+1\,$ above)
• The numerator is negative

Thus:

Observe that we did not compute actual values of the output near $\,x = -\frac 12\,$! There's no need—it would be working too hard. All we need to know is:

• The sign (positive or negative) of the numerator and denominator
• The denominator is small (close to zero)
• Dividing by increasingly small numbers give increasingly big numbers