REFERENCE ANGLES

• PRACTICE (online exercises and printable worksheets)

In the previous section, Special Triangles and Common Trigonometric Values, we kept saying
‘the (acute) angle between the $x$-axis and the hypotenuse (of the special triangle)’.

Quite a mouthful!

It's a really important angle, and in this section we'll give it a shorter name!

DEFINITION reference angle for $\,\theta$ Let $\,\theta\,$ (the ‘original’ angle) be any angle, laid off in the standard way: Start at the positive $x$-axis. Positive angles are swept out counterclockwise (start by going up). Negative angles are swept out clockwise (start by going down). The smallest angle beween the $x$-axis and the terminal (ending) side of $\,\theta\,$ is called the reference angle for $\,\color{blue}{\theta}\,$.

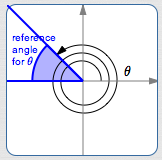
Example: a reference angle for a positive angle

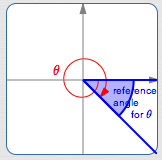
Example: a reference angle for a negative angle

Properties of the Reference Angle:

• Make sure you understand that there are two angles involved in this discussion:
  • the original angle (which might be really big)
  • the original angle's reference angle (which is always a manageable size)
• The original angle has an orientation: counterclockwise if positive, and clockwise if negative.
  However, the reference angle does not have any orientation. It just has a given size!
• The reference angle is always between $\,0^\circ\,$ and $\,90^\circ\,$:   $0^\circ\le\text{ reference angle }\le 90^\circ$
• In particular, reference angles are never negative .
• A reference angle can be zero:   this happens when the original angle's terminal point lies on the $x$-axis.
  That is, the reference angle is zero whenever the original angle's terminal point is either $\,(1,0)\,$ or $\,(-1,0)\,$.
• A reference angle can be $\,90^\circ\,$:   this happens when the original angle's terminal point lies on the $y$-axis.
  That is, the reference angle is $\,90^\circ\,$ whenever the original angle's terminal point is either $\,(0,1)\,$ or $\,(0,-1)\,$.

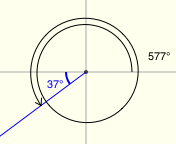
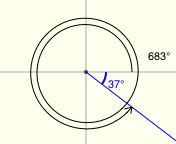
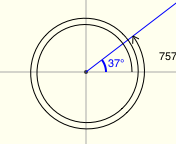
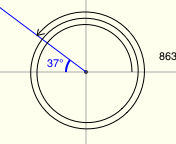
Examples of Reference Angles

There's a great applet for exploring reference angles at Math Open Reference.
The screenshots below were made from this applet, and have the following features:

• positive angles are shown in black
• negative angles are shown in red
• the reference angle is shown in blue

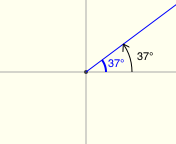
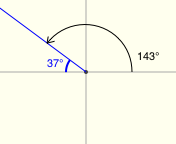
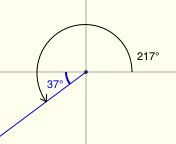
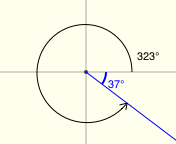
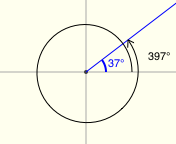
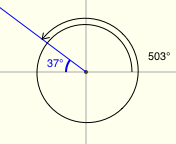
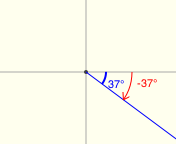
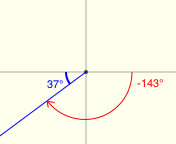
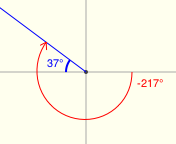
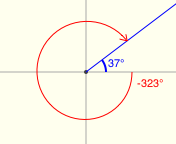
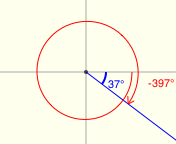
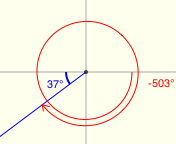
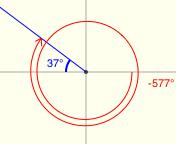
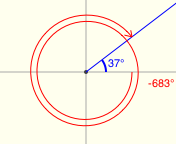
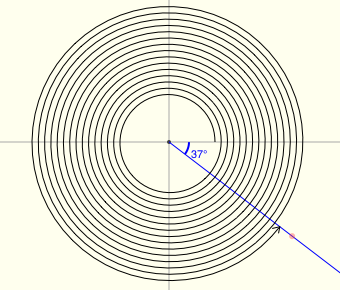
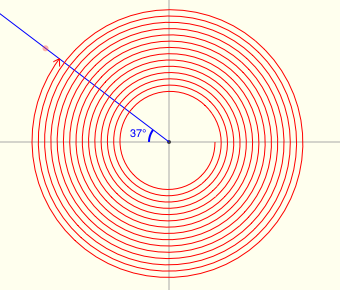
Reference Angles for Multiples of $\,90^\circ\,$

Angles that are multiples of $\,90^\circ\,$ have terminal points on the $x$-axis or $y$-axis.
In particular:

• Even multiples of $\,90^\circ\,$ (like $\,0\cdot 90^\circ\,$ or $\,-6\cdot 90^\circ\,$ or $\,4\cdot 90^\circ\,$) end up on the $x$-axis.
  Even multiples of $\,90^\circ\,$ have reference angle equal to zero.
• Odd multiples of $\,90^\circ\,$ (like $\,1\cdot 90^\circ\,$ or $\,11\cdot 90^\circ\,$ or $\,-5\cdot 90^\circ\,$) end up on the $y$-axis.
  Odd multiples of $\,90^\circ\,$ have reference angle equal to $\,90^\circ\,$.

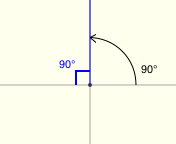
$\theta = 90^\circ$ The reference angle for $\theta$ is $90^\circ$.

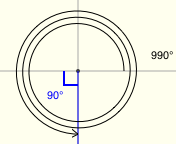
$\theta = 11\cdot90^\circ = 990^\circ$ The reference angle for $\theta$ is $90^\circ$.

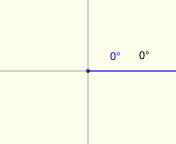
$\theta = 0^\circ$ The reference angle for $\theta$ is $0^\circ$.

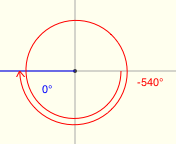
$\theta = -6\cdot 90^\circ = -540^\circ$ The reference angle for $\theta$ is $0^\circ$.

Size and Sign

Every real number has a size. Size is distance from zero, or absolute value.
Size is nonnegative (greater than or equal to zero).
For example, both $\,-5\,$ and $\,5\,$ have size $\,5\,$. The number $\,0\,$ has size $\,0\,$.

Every real number except zero has a sign (plus or minus).
Numbers to the right of zero are positive. Numbers to the left of zero are negative.
The number zero has no sign. Zero is not positive. Zero is not negative.

Size and sign together uniquely identify every nonzero real number.
What real number has size $\,3\,$ and is negative? The number $\,-3\,$.
What real number has size $\,7\,$ and is positive? The number $\,7\,$.

Finding Reference Angles and Quadrants

If the terminal point is on the $x$-axis or $y$-axis, then the trigonometric values are extremely easy to find.
For example, if the terminal point is $\,(1,0)\,$, then the cosine is $\,1\,$, the sine is $\,0\,$, and the other trigonometric values follow from their definitions.

For any angle that doesn't land on an axis, the following two pieces of information are sufficient to find all the trigonometric values:

• the reference angle (this is used to get the size of the trigonometric values)
• the quadrant that contains the terminal point (this is used to get the sign of the trigonometric values)

DISCLAIMER:
When dealing with angles and their reference angles, I'll often say things like
‘an angle in quadrant II’ instead of the more precise ‘an angle with terminal point in quadrant II’.

What follows is a way to find reference angles and quadrants.
It certainly isn't the only way, but it works.
It allows you to use smaller (more easily identifiable) numbers than some other methods.

• GET RID OF EXTRA ROTATIONS:
  To get started, take an unwieldy angle and ‘cut it down to size’:
  that is, get an angle between $\,-180^\circ\,$ and $\,180^\circ\,$ that has the same terminal point.
  This is done by getting rid of ‘extra’ $\,360^\circ\,$ rotations.
  Remember: if $\,\theta\,$is any angle (measured in degrees), then $\,\theta \pm k\cdot 360^\circ\,$ has the same terminal point, for $\,k = 1,2,3,\ldots \,$.
  
  For example, if $\,\theta = 863^\circ\,$, keep subtracting $\,360^\circ\,$:
  $863^\circ - 360^\circ - 360^\circ = 143^\circ$
  For positive angles, keep subtracting $\,360^\circ\,$ until you end up between $\,-180^\circ\,$ and $\,180^\circ\,$.
  
  Or, if $\,\theta = -863^\circ\,$, keep adding $\,360^\circ\,$:
  $-843^\circ + 360^\circ + 360^\circ = -123^\circ$
  For negative angles, keep adding $\,360^\circ\,$ until you end up between $\,-180^\circ\,$ and $\,180^\circ\,$.
• NOW, IT'S EASY TO SEE WHERE YOU ARE, AND WHAT THE REFERENCE ANGLE IS:
  Once you've got an angle between $\,-180^\circ\,$ and $\,180^\circ\,$, it's easy to see what quadrant you're in,
  and it's easy to determine the reference angle.
  
  Positive angles ( strictly between $\,0^\circ\,$ and $\,180^\circ\,$) put you in quadrants I and II.
  For example, $\,23^\circ\,$ is in quadrant I, and its reference angle is $\,23^\circ\,$.
  Or, $\,157^\circ\,$ is in quadrant II, and its reference angle is $\,180^\circ - 157^\circ = 23^\circ\,$.
  
  Negative angles (strictly between $\,0^\circ\,$ and $\,-180^\circ\,$) put you in quadrants III and IV.
  For example, $\,-23^\circ\,$ is in quadrant IV, and its reference angle is $\,23^\circ\,$.
  Or, $\,-157^\circ\,$ is in quadrant III, and its reference angle is $\,180^\circ - 157^\circ = 23^\circ\,$.
  
  I could include formulas for the reference angle in each case, but I won't.
  (If I did, some students would memorize these formulas.)
  With a quick sketch, it will be obvious in all cases what the reference angle is!

EXAMPLE:
Renaming Trigonometric Values using Reference Angle/Quadrant

Let $\,\theta = 1747^\circ\,$.

1. Cut $\,\theta\,$ down to size: that is, get an angle between $\,-180^\circ\,$ and $\,180^\circ\,$ with the same terminal point.
2. Find the reference angle and quadrant for $\,\theta\,$.
3. Use the reference angle to find the size of $\,\sin \theta\,$ and $\,\cos \theta\,$.
4. Use the quadrant to find the sign of $\,\sin \theta\,$ and $\,\cos \theta\,$.
5. Rename $\,\sin 1747^\circ\,$ and $\,\cos 1747^\circ\,$ using size (reference angle) and sign (quadrant).

1. There are a bunch of ‘extra rotations’ in $\,1747^\circ\,$.   How many?   Well, $\displaystyle\frac{1747^\circ}{360^\circ} \approx 5\,$ (rounded to the nearest whole number).
   Then, $1747^\circ - 5\cdot 360^\circ = -53^\circ$, which is between $\,-180^\circ\,$ and $\,180^\circ\,$.
   
   
   Let $\,\theta\,$ be any nonzero angle, measured in degrees.
   Divide the absolute value of $\,\theta\,$ by $\,360^\circ\,$, and round the result to the nearest whole number—call this whole number $\,k\,$.
   If $\,\theta > 0\,$, then $\,\theta - k\cdot 360^\circ\,$ is always an angle between $\,-180^\circ\,$ and $\,180^\circ\,$.
   If $\,\theta < 0\,$, then $\,\theta + k\cdot 360^\circ\,$ is always an angle between $\,-180^\circ\,$ and $\,180^\circ\,$.
   Why?
   
   Here's the simple idea, which will hopefully convince you that this always works:

   • The number $\displaystyle\,h := \frac{|\theta|}{360^\circ}\,$ answers the question:   How many chunks of size $\,360^\circ\,$ are in $\,\theta\,$?
     Unless $\,\theta\,$ is a multiple of $\,360^\circ\,$, then $\,h\,$ will have have a decimal part.
     If the decimal part is $\,0.5\,$ or more, we'll round up to get $\,k\,$.
     If the decimal part is less than $\,0.5\,$, we'll round down to get $\,k\,$.
   • Here's a specific example that shows how the general argument would go:
     Suppose $\,\theta > 0\,$ and $\,\displaystyle\frac{\theta}{360^\circ} = 5.6\,$ (so that $\,\theta = 5.6\cdot 360^\circ\,$).
     We'd round up in this case, letting $\,k = 6\,$.
     Then:   $ \theta - 6\cdot 360^\circ = 5.6\cdot 360^\circ - 6\cdot 360^\circ = -0.4\cdot 360^\circ $
     Thus, the size of $\,\theta - 6\cdot 360^\circ\,$ is less than half of $\,360^\circ\,$! Just what we want!
2. Clearly, $-53^\circ\,$ lies in quadrant IV;   the reference angle is $\,53^\circ\,$.
3. The reference angle determines the size of the trigonometric values.
   Since the reference angle for $\,\theta = 1747^\circ\,$ is $\,53^\circ\,$:
   the size of $\,\sin 1747^\circ\,$ is $\,\sin 53^\circ\,$;
   the size of $\,\cos 1747^\circ\,$ is $\,\cos 53^\circ\,$
4. The quadrant determines the sign of the trigonometric values.
   In quadrant IV, sine ($y$-value) is negative and cosine ($x$-value) is positive
5. Thus:
   $\,\sin 1747^\circ = -\sin 53^\circ\,$
   $\,\cos 1747^\circ = \cos 53^\circ\,$

EXAMPLE:
Renaming Trigonometric Values using Reference Angle/Quadrant

Rename $\,\sin (-2252^\circ)\,$ and $\,\cos (-2252^\circ)\,$ using reference angle and quadrant.

SOLUTION:

$\displaystyle\frac{2252^\circ}{360^\circ} \approx 6\,$

$-2252^\circ + 6\cdot 360^\circ = -92^\circ$

quadrant: III (both sine and cosine are negative)

reference angle: $\,180^\circ - 92^\circ = 88^\circ$

$\,\sin (-2252^\circ) = -\sin 88^\circ\,$
$\,\cos (-2252^\circ) = -\cos 88^\circ\,$