Finding Inverse Functions (when there's only one $\,x\,$ in the formula)

Index card: 23a

This lesson will be more meaningful if you fully understand the concepts in these prior lessons:

• Using a Function Box ‘Backwards’
• One-to-One Functions
• Undoing a One-to-One Function; Inverse Functions
• Properties of Inverse Functions

Every one-to-one function $\,f\,$ has an inverse, denoted by $\,f^{-1}\,,$ that ‘undoes’ what $\,f\,$ does.

In this lesson and the next, we look at two common techniques for getting a formula for $\,f^{-1}\,.$

The ‘mapping diagram method’ for finding an inverse is discussed below. It only works when the formula for $\,f\,$ has exactly one appearance of the input variable.

For example, the function  $\,f(x) = 5\color{blue}{x} - 4\,$  has only one $\,\color{blue}{x}\,$ in its formula.

However, the function  $\displaystyle\,g(x) = \frac{1-3\color{red}{x}}{5+2\color{red}{x}}\,$  has two appearances of the variable $\,\color{red}{x}\,.$

The ‘mapping diagram method’ will work for $\,f\,,$ but not for $\,g\,.$

This author strongly prefers the ‘mapping diagram method’ because it emphasizes the fact that $\,f\,$ does something, and $\,f^{-1}\,$ undoes it.

The method discussed in the next lesson is more widely applicable, but tends to be quite mechanical. If you're not careful, you can just ‘go through the motions’ and forget the underlying idea!

Example: the ‘Mapping Diagram’ Method

In this example, the ‘mapping diagram’ method for finding the inverse is applied to the function $\,f(x) = 5x - 4\,.$

1. The formula for $\,f\,$ contains exactly one appearance of $\,x\,.$

2. What does $\,f\,$ do to this input $\,x\,$? It multiplies by $\,5\,,$ and then subtracts $\,4\,.$ See the blue part of the mapping diagram below.

   Need some elementary practice looking at a formula and interpreting it as a sequence of operations? Going From an Expression to a Sequence of Operations

3. How do we ‘undo’ each of the things that $\,f\,$ did, in reverse order?

   Moving from right to left:

   • ‘Subtract $\,4\,$’ is undone by ‘add $\,4\,$’
   • ‘Multiply by $\,5\,$’ is undone by ‘divide by $\,5\,$’

   See the red part of the mapping diagram below.

4. The function $\,f^{-1}\,$ must first add $\,4\,,$ and then divide by $\,5\,.$

   The formula is:  $\displaystyle\,f^{-1}(x) = \frac{x+4}5\,$

   Need some elementary practice writing a sequence of operations as an expression? Going From a Sequence of Operations to an Expression

The ‘Mapping Diagram’ Method For Finding an Inverse

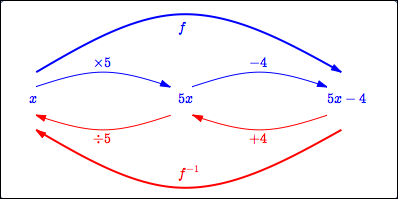
Finding the inverse of $\,f(x) = 5x-4\,$:

Think about what $\,f\,$ does, and then ‘undo’ it, in reverse order.

Checking an Inverse Problem with Composition

Want confidence that your inverse is correct? Verify either one of the following conditions (your choice):

• $f(f^{-1}(x)) = x$
• $f^{-1}(f(x)) = x$

You only need to check one—if it works, the other must also. Here's one proof. The other proof is similar.

Suppose that $\,f\,$ is one-to-one, and $\,f(f^{-1}(y)) = y\,$ for all $\,y\in\text{ran}(f)\,.$

Since $\,f(x)\in\text{ran}(f)\,$ whenever $\,x\in\text{dom}(f)\,,$ we have $\,f\bigl(f^{-1}(f(x)\bigr) = f(x)\,$ for all $\,x\in\text{dom}(f)\,.$

But $\,f\,$ is one-to-one, so $\,f(z) = f(w)\,$ implies $\,z=w\,.$ Thus, $\,f^{-1}(f(x)) = x\,$ for all $\,x\in\text{dom}(f)\,.$

Making this check is also great practice with function composition, so if you have time, it's highly recommended. Both conditions are checked here for your easy perusal:

Sometimes You Have Choices for How to Think of ‘Undoing’

Sometimes you have a choice about how you think of ‘undoing’ something.

For example, ‘multiply by $\,5\,$’ can be undone by ‘divide by $\,5\,$’. Or, ‘multiply by $\,5\,$’ can be undone by ‘multiply by $\,\frac{1}{5}\,$’.

As a second example, ‘multiply by $\,-1\,$’ can be undone by ‘divide by $\,-1\,$’. Or, ‘multiply by $\,-1\,$’ can be undone by ‘multiply by $\,-1\,$’, since multiplying by $\,-1\,$ twice in succession returns you to where you started!

Sometimes, a particular choice can make a formula look a bit simpler.

Example: Simpler Notation for the ‘Mapping Diagram’ Method

You don't actually have to draw the mapping diagram to use this method. Just make a list of what $\,f\,$ does, and how to ‘undo’ each.

Even better—once you get good at this method, you may be able to look at the formula for $\,f\,$ and write the inverse immediately!

Let's illustrate by finding the inverse of $\,f(x) = 4 - \root 3\of{x+1}\,.$

First, rewrite it as $\,f(x) = -1\cdot\root 3\of{x+1} + 4\,,$ to make the sequence of operations a bit clearer.

Implement the ‘undo’ list in reverse order:

Easy!

Finding Inverses at Wolfram Alpha

Or, you could zip up to https://www.wolframalpha.com and type in something like:

inverse of y = 4 - cube root of (x+1)

Make sure your entry is confirmed with:

$\,y(x) = 4 - \root 3\of{x+1}\,$

You will likely be informed that:

$\,x(y) = -y^3 + 12y^2 - 48y + 63\,$

They're using function notation:  $\,x(y)\,$ indicates that $\,x\,$ is a function of $\,y\,.$ That is, for each value of $\,y\,$ there is a unique value of $\,x\,.$

They're also using a different name for the inverse. Note that:

Isn't Wolfram Alpha wonderful?