Graphing Generalized Sines and Cosines, Like $\,y = a\sin k(x\pm b)\,$ and $\,y = a\cos (kx\pm B)\,$ (Part 1)

(This page is Part 1. Click here for Part 2.)

The prior section explored the (basic) graphs of $\,y = \sin x\,$ and $\,y = \cos x\,.$ However, these trigonometric functions frequently appear in ‘transformed’ versions.

You might see, for example: $$y = -1.5\sin \frac{1}{2}(x - \pi)$$ or $$y = \frac{1}{3}\cos (4x + 5)$$

The observations and techniques discussed in this section will allow you to reliably, quickly, and efficiently graph any function of the following forms, without memorizing a bunch of different formulas :

Notice, in particular, that the arguments $\,k(x\pm b)\,$ (first row) and $\,kx\pm B\,$ (second row) are different. For example, $\,2(x-5)\,$ is different from $\,2x - 5\,.$ These input types are commonly seen in applications.

In mathematics, the word ‘argument’ is often used to refer to the input of a function. For example, the argument of the sine function in the expression ‘$\,\sin k(x\pm b)\,$’ is $\,k(x\pm b)\,.$ As a second example, the argument of the cosine function in the expression ‘$\,\cos (kx\pm B)\,$’ is $\,kx\pm B\,.$

Any argument with only two types of terms—an $x$-term and a constant term—can be handled with the four-step graphing process discussed below. With this four-step technique, you don't need to identify which type of argument you're working with; you only need to identify the coefficient of the $x$-term.

For example, the four-step technique can be used to graph (say) $\,\displaystyle y = -9\sin\frac{\pi + 5x}{8}\,.$ Why?  The argument has only an $x$ term and a constant term.

Here, $\,k = \frac 58\,.$ Why?  Rewrite the argument (as needed) to see that the coefficient of $\,x\,$ is $\,\color{red}{\frac 58}\,$:

The following two key observations will lead to an efficient approach. Click the Show/Hide buttons for additional information.

Observation #1

Each generalized function is the result of graphical transformation(s) chosen from:

• Horizontal stretch/shrink
• Shift right/left
• Vertical stretch/shrink
• Reflection about $x$-axis

Here is a graphical example to illustrate. For clarity, only one period of each graph is shown.

Keep in mind that transformations involving $\,x\,$ are counter-intuitive! For example, you might expect that replacing every $\,x\,$ by $\,\frac{x}{2}\,$ would result in the period being cut in half. In reality, the period is doubled! (Review earlier graphical transformation discussions to see why!)

Desired graph: $\,y = -1.5\sin \frac{1}{2}(x - \pi)$

$y = \sin x$

(The basic model)

$y = \sin \frac{1}{2}x = \sin\frac{x}{2}$

Replace every $\,x\,$ by $\,\frac{x}{2}\,.$ This gives a horizontal stretch:  points $\,(x,y)\,$ move to $\,(2x,y)\,.$

$y = \sin\frac{1}{2}(x - \pi)$

Replace every $\,x\,$ by $\,x - \pi\,.$ This shifts the graph $\,\pi\,$ to the right:  points $\,(x,y)\,$ move to $\,(x+\pi,y)\,.$

$y = 1.5\sin\frac{1}{2}(x - \pi)$

Multiply previous $y$-values by $\,1.5\,.$ This gives a vertical stretch:  points $\,(x,y)\,$ move to $\,(x,1.5y)\,.$

$y = -1.5\sin\frac{1}{2}(x - \pi)$

Multiply previous $y$-values by $\,-1\,.$ This reflects about the $x$-axis:  points $\,(x,y)\,$ move to $\,(x,-y)\,.$

The only transformation that changes the period is the horizontal stretch.

In general, a horizontal stretch/shrink (replacing every $\,x\,$ by $\,kx\,$) causes points $\,(x,y)\,$ to move to $\,(\frac{x}{k},y)\,.$ This changes a period of $\,2\pi\,$ to a new period of $\,\frac{2\pi}{k}\,.$

In this example, $\,k = \frac{1}{2}\,.$ Thus, the new period is:

$$\frac{2\pi}{k} = \frac{2\pi}{1/2} = 4\pi$$

Here is a second example, in tabular form:

Equation	$y = \cos x$
Do This to Previous Equation...	(Starting point)
Graphical Result	Basic model
One Cycle of Graph

Equation	$y = \cos (x+5)$
Do This to Previous Equation...	Replace every $\,x\,$ by $\,x+5$
Graphical Result	Shift left $\,5\,,$ $\,(x,y)\mapsto (x-5,y)$
One Cycle of Graph

Equation	$y = \cos (4x+5)$
Do This to Previous Equation...	Replace every $\,x\,$ by $\,4x$
Graphical Result	Horizontal shrink, $\,(x,y)\mapsto (\frac x4,y)$ (This is the only step that changes the period.)
One Cycle of Graph

Equation	$y = \frac 13\cos (4x+5)$
Do This to Previous Equation...	Multiply previous $y$-value by $\,\frac 13$
Graphical Result	Vertical shrink, $\,(x,y)\mapsto (x,\frac 13y)$
One Cycle of Graph

Observation #2

The only transformation that changes the period is the horizontal stretch/shrink.

The horizontal stretch/shrink is caused by replacing every $\,x\,$ by $\,kx\,,$ which causes points $\,(x,y)\,$ to move to new points $\,(\frac{x}{k},y)\,.$

For $\,k \gt 0\,,$ the horizontal stretch/shrink changes the original period $\,2\pi\,$ to the new period $\,\frac{2\pi}{k}\,.$

If $\,k \lt 0\,,$ rewrite first, using (as needed):

• Sine is odd:  $\,\sin(-x) = -\sin x\,$

  Graph:  $y = \sin (3 - x)$

  (Note that the coefficient of $\,x\,$ is $\,-1\,.$ )

  So, rewrite:

  $$ \begin{align} \sin(3-x) &= \sin \bigl(-(x-3)\bigr)\cr &\qquad \text{(factor out $\,-1\,$)}\cr &= -\sin (x-3)\cr &\qquad \text{(sine is odd)} \end{align} $$

  Now, graph the equivalent equation:

  $$y = -\sin (x-3)$$

• Cosine is even:  $\,\cos (-x) = \cos x$

  Graph:  $y = \cos (-5x+3))$

  (Note that the coefficient of $\,x\,$ is $\,-5\,.$ )

  So, rewrite:

  $$ \begin{align} \cos(-5x+3) &= \cos \bigl(-(5x-3)\bigr)\cr &\qquad \text{(factor out $\,-1\,$)}\cr &= \cos(5x-3)\cr &\qquad \text{(cosine is even)} \end{align} $$

  Now, graph the equivalent equation:

  $$y = \cos (5x-3)$$

This leads us to:

The Four-Step Graphing Process

You'll graph only one period. By extending periodically, this uniquely defines the entire curve.

General Procedure

Example:

Graph $\,y = -7\cos (3-5x)$

Step 1:  Check that $\,k\,$ is Positive

The coefficient of the $x$-term in the argument is denoted by $\,k\,.$ Make sure that $\,k \gt 0\,.$ If not, rewrite (as above), using the odd/even properties of sine/cosine.

Example (continued):

Initially, the coefficient of the $x$-term is $\,-5\,.$ Rewrite:

$$ \begin{align} &\cssId{s62}{-7\cos (3-5x)}\cr\cr &\qquad \cssId{s63}{=} \cssId{s64}{-7\cos\bigl(-(5x-3)\bigr)}\cr &\qquad\qquad \text{(distributive law)}\cr\cr &\qquad \cssId{s65}{=} \cssId{s66}{-7\cos (5x-3)}\cr &\qquad\qquad \text{(cosine is even)} \end{align} $$

Instead, graph:  $y = -7\cos (5x-3)$

(So, $\,k = 5\,.$ )

Step 2:  Starting Point

Each sine/cosine curve starts a ‘natural’ cycle when its argument is zero. Compute the value of $\,x\,$ that makes the argument equal to zero. This is your starting point; call it $\,S\,$ and mark it on a number line.

Example (continued):

Find $\,S\,$:

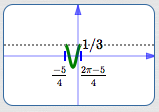
$$ \begin{gather} \cssId{s74}{5x-3 = 0}\cr \cssId{s75}{5x = 3}\cr \cssId{s76}{x = \frac{3}{5}} \end{gather} $$

So, $\,S = \frac{3}{5}\,.$

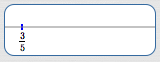
Step 3:  Ending Point

Compute the new period, $\displaystyle\,\frac{2\pi}{k}\,.$

The cycle that starts at $\,S\,$ ends at $\displaystyle\,E := S +\frac{2\pi}{k}\,.$

In other words, one complete cycle occurs on the interval: $$[S\ ,\ \underbrace{S +\frac{2\pi}{k}}_{E}]$$

Mark the ending point, $\,E\,,$ on the number line.

Divide the interval from starting point to ending point into four equal parts, to make it easier to draw in the basic cycle.

Example (continued):

$$\cssId{s84}{k = 5}$$ $$\cssId{s85}{\displaystyle\text{period} = \frac{2\pi}{k} = \frac{2\pi}{5}}$$ $$\cssId{s86}{\displaystyle E := S + \frac{2\pi}{k} = \frac{3}{5} + \frac{2\pi}{5}}$$

Step 4:  Draw in the Basic Cycle; Adjust (as needed) for Amplitude/Flip

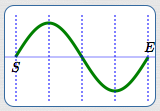
Basic sine cycle

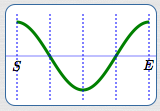
Basic cosine cycle

As discussed in the next section, amplitude is the distance from the $x$-axis to the highest (or lowest) part of the graph.

The amplitude of $\,y = \sin x\,$ and $\,y = \cos x\,$ is $\,1\,.$ Vertical scaling by a factor of $\,a\,$ causes the amplitude to change to $\,|a|\,.$

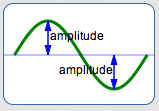
Vertical scaling by a factor of $\,-1\,$ causes reflection about the $x$-axis (i.e., a ‘flip’).

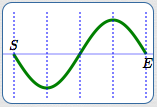
Basic sine cycle, flipped

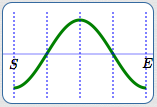
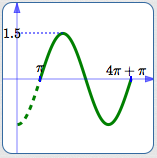
Basic cosine cycle, flipped

Draw in the basic cosine cycle, flipped.

The amplitude is $\,7\,.$

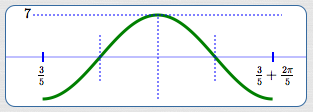
To emphasize:

In this graph of (one cycle of) $\,y = -7\cos (5x-3)\,$:

• The fact that it is a cosine curve, $\,y = -7\color{red}{\cos}(5x-3)\,,$ causes you to use the basic cosine cycle.
• The leading minus sign, $\,{\bf\color{red}{-}}7\,,$ causes the cycle to be flipped.
• The amplitude is $\,|-7|\, = 7\,.$