audio read-through Review of Lines and Slopes of Lines

For success in Precalculus and Calculus, you must have an extremely high comfort level working with lines and slopes of lines. This lesson offers an in-a-nutshell review of essential concepts. It might be all that you need!

For a thorough review, however, go through the following lessons in order. Be sure to click-click-click the exercises in each section to check your understanding.

SLOPE OF LINES essential concepts
  • ‘Slope’ is a number that measures the ‘steepness’ of a line; it is conventionally denoted by the variable $\,m\,.$
  • Let $\,(x_1,y_1)\,$ and $\,(x_2,y_2)\,$ be two points on a non-vertical line. Then: $$ \cssId{s12}{m = \text{slope}} \cssId{s13}{= \frac{\text{rise}}{\text{run}}} \cssId{s14}{= \frac{y_2-y_1}{x_2-x_1}}$$
  • ‘Rise’ denotes vertical travel:
    • up is positive
    • down is negative
  • ‘Run’ denotes horizontal travel:
    • to the right is positive
    • to the left is negative
  • To find the slope of any non-vertical line:
    • Choose any two points.
    • Travel from one to the other, going vertically first (the rise) and horizontally second (the run).
    • Take the rise, and divide by the run.
  • Horizontal lines have slope zero ($m = 0$).
  • Vertical lines have no slope (the slope does not exist, due to division by zero).
  • Two nonvertical lines are parallel if and only if they have the same slope.
  • Perpendicular lines have slopes that are opposite reciprocals. For example, lines with slopes $\,3\,$ and $\,-\frac 13\,$ are perpendicular.
  • Going from left to right:
    • Uphill lines have positive slopes.
    • Downhill lines have negative slopes.
    • Steep lines have big slopes (numbers far away from zero).
    • Gradual lines have small slopes (numbers close to zero).
horizontal line, zero slope, equation y = k Horizontal line,
zero slope,
equation $\,y = k\,$
vertical line, no slope, equation x = k Vertical line,
no slope,
equation $\,x = k\,$

Uphill Lines, Positive Slopes

gradual uphill, small positive slope Gradual uphill,
small positive slope
steep uphill, large positive slope 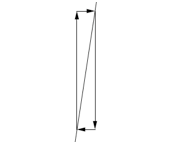Steep uphill,
large positive slope

Downhill Lines, Negative Slopes

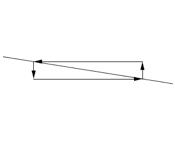gradual downhill, small negative slope Gradual downhill,
small negative slope
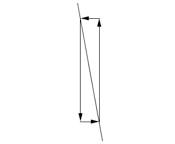steep downhill, large negative slope Steep downhill,
large negative slope
LINES useful forms

  • Standard form, $\,ax + by + c = 0$

    • As long as $\,a\,$ and $\,b\,$ are not both zero, then $\,ax + by + c = 0\,$ graphs as a line.
    • When $\,a = 0\,$ there is no $\,x\,$ term, and the line is horizontal. Horizontal lines can be written in the form $\,y = k\,.$
    • When $\,b = 0\,$ there is no $\,y\,$ term, and the line is vertical. Vertical lines can be written in the form $\,x = k\,.$

  • Slope-intercept form, $\,y = mx + b$

    • Every equation of the form $\,y=mx+b\,$ graphs as a non-vertical line.
    • The slope of the line is $\,m\,$ (the coefficient of the $\,x\,$ term).
    • The line crosses the $y$-axis at the point $\,(0,b)\,.$

  • Point-slope form, $\,y - y_1 = m(x - x_1)$

    • This line has slope $\,m\,$ and passes through the point $\,(x_1,y_1)\,.$
LINES key concepts

  • Intercepts:

    • To find an $x$-intercept: set $\,y = 0\,$ and solve for $\,x\,.$
    • To find a $y$-intercept: set $\,x = 0\,$ and solve for $\,y\,.$

  • For lines, equal changes in the input give rise to equal changes in the output. If $\,x\,$ changes by $\,\Delta x\,$ (delta $\,x\,$), then $\,y\,$ changes by $\,m\Delta x\,.$

    That is, the outputs change $\,m\,$ times as fast as the inputs (where $\,m = \text{slope}\,$).

    Example: If a line has slope $\,3\,,$ the outputs change $\,3\,$ times as fast as the inputs.

Concept Practice