Basic Function Models You Must Know (Part 1)

(This page is Part 1. Click here for Part 2.)

There are many functions that you should have on your fingertips, in the following sense:

• Given the function, you should immediately be able to sketch its graph (indicating all important features).
• Given the graph, you should immediately recognize the (probable) function.

The purpose of this lesson is to give you practice with these basic models, which will be used freely throughout the rest of the course.

Some of these functions (e.g., the trigonometric functions) are not studied until later in the course, but you can begin to familiarize yourself with the graphs now.

First review Basic Models You Must Know. The current lesson builds on this prior information.

Most graphs are shown in the same window, from $\,-5\,$ to $\,5\,$ on the $x$-axis, and from $\,-5\,$ to $\,5\,$ on the $y$-axis. You may use the navigation arrows (bottom right on each graph) to zoom or move around.

Drag the point on each graph to see coordinates. The scales on the $x$-axis and $y$-axis are identical. That is, a distance of $\,1\,$ on the $x$-axis is the same as a distance of $\,1\,$ on the $y$-axis.

Click on Each Link for Additional Information

the identity function
$f(x) = x$

the cubing function
(and higher odd powers)
$f(x) = x^3\,,$ $f(x) = x^{\text{odd}}$

the absolute value function
$f(x) = |x|$

the sine function
$f(x) = \sin(x)$

constant functions
$f(x) = k\,,$ $\,k\in\Bbb R$

the reciprocal function
$\displaystyle f(x) = \frac 1x\,$

the natural exponential function
$\displaystyle f(x) = {\text{e}}^x$

the cosine function
$\displaystyle f(x) = \cos(x)$

the squaring function
(and higher even powers)
$f(x) = x^2\,,$ $f(x) = x^{\text{even}}$

the square root function
$f(x) = \sqrt{x}\,$

the natural logarithm function
$f(x) = \ln(x)\,$

the tangent function
$f(x) = \tan(x)\,$

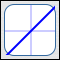
The Identity Function

the identity function
$f(x) = x$

• The identity function takes an input, does nothing to it, and gives back the same thing as its output. That is, the identity function preserves the identity of its input—hence its name is appropriate.
• $\,\text{dom}(f) = \mathbb{R}$
  $\,\text{ran}(f) = \mathbb{R}$
• End behavior:
  as $\,x \rightarrow \infty\,,$ $\,y\rightarrow\infty$
  as $\,x\rightarrow -\infty\,,$ $\,y\rightarrow -\infty$
• $f$ increases everywhere

Constant Functions

constant functions
$f(x) = k\,,\ \ k\in\Bbb R$
(here, $k = 3$)

• A constant function takes an input, and returns a specific real number—a constant. In the graph above, the function always returns the number $\,3\,.$

  Constant functions are extremely boring—they ignore the input, and always return the same output.

• $\,\text{dom}(f) = \mathbb{R}$

• The range of a constant function is a set containing only one number.

  For the constant function shown:  $\text{ran}(f) = \{3\}$

• Important feature: Every constant function graphs as a horizontal line.

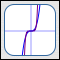
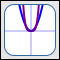
The Squaring Function

• The squaring function takes an input and squares it (i.e., multiplies it by itself).
• All functions of the form $\,f(x) = x^n\,$ where $\,n\in\{2,4,6,\ldots\,\}\,$ (that is, $\,f(x) = x^{\text{even}}\,$) have the same general shape, domain, range, and end behavior.
• $\,\text{dom}(f) = \mathbb{R}$
  $\,\text{ran}(f) = [0,\infty)$
• End behavior:
  as $\,x \rightarrow \infty\,,$ $\,y\rightarrow\infty$
  as $\,x\rightarrow -\infty\,,$ $\,y\rightarrow \infty$
• $f\,$ decreases on $\,(-\infty,0]\,$ and increases on $\,[0,\infty)$
• Important features:
  • There is a horizontal tangent line at the point $\,(0,0)\,.$
  • All graphs pass through the points $(0,0)$, $(1,1)$ and $(-1,1)\,.$
  • As the even exponent gets bigger, the graph gets flatter (closer to zero) on the interval $\,(-1,1)\,.$
  • As the even exponent gets bigger, the graph gets steeper (closer to vertical) to the right of $\,1\,$ and to the left of $\,-1\,.$

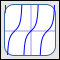
The Cubing Function

• The cubing function takes an input and cubes it ($\,x^3 = x\cdot x\cdot x\,$).
• All functions of the form $\,f(x) = x^n\,$ where $\,n\in\{3,5,7,\ldots\,\}\,$ (that is, $\,f(x) = x^{\text{odd}}\,$) have the same general shape, domain, range, and end behavior.
• $\,\text{dom}(f) = \mathbb{R}$
  $\,\text{ran}(f) = \mathbb{R}$
• End behavior:
  as $\,x \rightarrow \infty\,,$ $\,y\rightarrow\infty$
  as $\,x\rightarrow -\infty\,,$ $\,y\rightarrow -\infty$
• $f\,$ increases everywhere
• Important features:
  • There is a horizontal tangent line at the point $\,(0,0)\,.$
  • All graphs pass through the points $(0,0)$, $(1,1)$ and $(-1,-1)\,.$
  • As the odd exponent gets bigger, the graph gets flatter (closer to zero) on the interval $(-1,1)\,.$
  • As the odd exponent gets bigger, the graph gets steeper (closer to vertical) to the right of $\,1\,$ and to the left of $\,-1\,.$

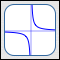
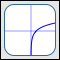
The Reciprocal Function

the reciprocal function
$\displaystyle f(x) = \frac 1x$

• The reciprocal function takes the reciprocal (i.e., multiplicative inverse) of an input.
• $\,\text{dom}(f) = (-\infty,0) \cup (0,\infty)$
  $\,\text{ran}(f) = (-\infty,0) \cup (0,\infty)$
• End behavior:
  as $\,x \rightarrow \infty\,,$ $\,y\rightarrow 0$
  as $\,x\rightarrow -\infty\,,$ $\,y\rightarrow 0$
• Behavior near zero:
  as $\,x \rightarrow 0^{+}\,,$ $y\rightarrow\infty$
  as $\,x \rightarrow 0^{-}\,,$ $y\rightarrow -\infty$
• $f$ decreases on $\,(-\infty,0)\,$
  $f$ decreases on $\,(0,\infty)\,$

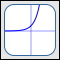
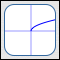
The Square Root Function

the square root function
$f(x) = \sqrt{x}$

• The square root function takes the square root of an input.
• $\text{dom}(f) = [0,\infty)$
  $\text{ran}(f) = [0,\infty)$
• End behavior:
  as $\,x \rightarrow \infty\,,$ $\,y\rightarrow\infty$
  
• $f$ increases everywhere on its domain
• Important feature: There is a vertical tangent line at the point $\,(0,0)\,.$

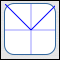
The Absolute Value Function

the absolute value function
$f(x) = |x|$

• The absolute value function takes the absolute value of an input. If an input is positive or zero, then it is not changed. If an input is negative, then the function returns its opposite. Consequently, the absolute value always returns a nonnegative number.
• $\,\text{dom}(f) = \Bbb R$
  $\,\text{ran}(f) = [0,\infty)$
• End behavior:
  as $\,x \rightarrow \infty\,,$ $\,y\rightarrow\infty$
  as $\,x \rightarrow -\infty\,,$ $\,y\rightarrow\infty$
  
• $f$ decreases on $\,(-\infty,0]$ and increases on $\,[0,\infty)$
• Important feature: There is a ‘kink’ (i.e., a sharp change in direction) at the point $\,(0,0)\,.$ That is, if you imagine yourself walking along the graph, going from left to right, then at the instant you are passing through the point $\,(0,0)\,,$ you will abruptly change direction.