 Extreme Values of Functions (Max/Min)
Extreme Values of Functions (Max/Min)
Roughly, ‘extreme values’ are the $y$-values of high/low points on a graph.
You also usually want to know the $x$-value(s) where these high/low points occur.
The $y$-value of a highest point is called a maximum value.
The $y$-value of a lowest point is called a minimum value.
As illustrated below, the ONLY places that extreme values can occur are at horizontal tangent lines, kinks/breaks, and endpoints.
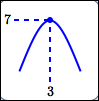
maximum value is $\,7\,$; |
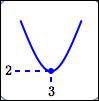
minimum value is $\,2\,$; |
The plural of maximum is maxima.
The plural of minimum is minima.
Maxima/minima can occur at horizontal tangent lines.
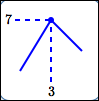
maximum value is $\,7\,$; |
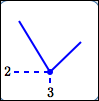
minimum value is $\,2\,$; |
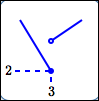
A ‘kink’ is a sudden change in direction.
Maxima/minima can occur at kinks.
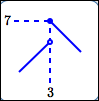
maximum value is $\,7\,$; |
minimum value is $\,2\,$; |
Imagine tracing a graph with a pencil.
A ‘break’ is a place where you have to pick up the pencil.
Maxima/minima can occur at breaks.
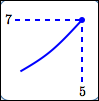
maximum value is $\,7\,$; |
minimum value is $\,2\,$; |
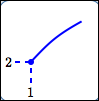
Maxima/minima can occur at endpoints.
The only places that extreme values can occur are at horizontal tangent lines, kinks/breaks, and endpoints.
But, you don't have to have an extreme value at such places!
In all the examples below, there are greater and lesser values arbitrarily close by.
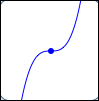
Horizontal tangent line:
no extreme value here

Kink:
no extreme value here
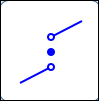
Break:
no extreme value here
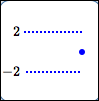
Endpoint:
no extreme value here
To the left of the endpoint, the function oscillates: it's $\,2\,$ for rational inputs, and $\,-2\,$ for irrational inputs.
You have to work hard to get an example of an endpoint that's not a max or min!
A Discussion of Extreme Values from a Non-Graphical Viewpoint
Suppose you have a function $\,f\,.$ A function is a rule—it takes an input, does something to it, and gives a corresponding output. The function $\,f\,$ can be viewed as a box:
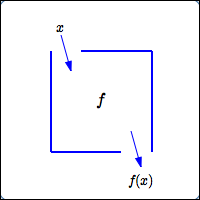
- Drop an input $\,x\,$ in the top
- $f\,$ does something to the input
- The corresponding output $\,f(x)\,$ drops out the bottom
For extreme value questions, you have the following scenario:
You're interested in a particular set of inputs—it might be the entire domain; it might be some interval.
You drop these inputs of interest into the function box, and get a corresponding pile of outputs.
Take a look at this output pile:
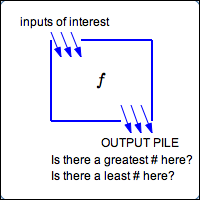
-
Is there a greatest number in the output pile?
That is, can you pick up a number that is greater than or equal to all the other numbers in the pile?
If so, we call this number an extreme value—in this case, a maximum.
-
Is there a least number in the output pile?
That is, can you pick up a number that is less than or equal to all the other numbers in the pile?
If so, we call this number an extreme value—in this case, a minimum.
In both cases, we likely want to know what input(s) gave rise to these ‘extreme’ outputs.
Extreme value questions have to do with finding the greatest/least values of the output of a function, and figuring out what input(s) they came from.
Greatest/Least Overall? Or Just Close By? (Global versus Local Max/Min)
Sometimes you're interested in highest/lowest values overall (like at B, E, and F). These are called global (or absolute) max/min.
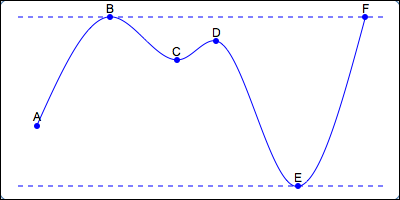
Sometimes you're interested in ‘local’ highest/lowest values (like at A, C, and D). These are called local (or relative) max/min. These are highest/lowest, provided you don't look too far away!
[Note: You'll learn in Calculus that a global max is also a local max, and a global min is also a local min.]
Some people like the terminology global/local. Others like absolute/relative. You choose!
Calculus provides language and tools to enable precise discussions of extreme values and related concepts. The informal language used here (e.g., ‘high/low points’, ‘breaks’, ‘kinks’) will all be made precise in Calculus. This section is only an informal introduction.
The field of Operations Research is devoted to maximizing or minimizing real-world objectives. Maximize profits. Minimize costs. Minimize the amount of material needed to construct a box with a specified volume. Extreme values have extreme applicability!
And Finally—You May Not Have Extreme Values!
You may not have any extreme values. You might have a max, but not a min. You might have a min, but not a max.
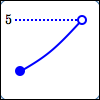
In the graph shown, the number $\,5\,$ is ‘trying to be’ the maximum value. But, there's no $\,5\,$ in the output pile, because the point isn't there!
For example, you could pick up a $\,4.9\,$ from the output pile—but this wouldn't be greatest, because there's a $\,4.99\,$ there!
And $\,4.99\,$ isn't greatest, because there's a $\,4.999\,$ there (and so on).
There's an important theorem in Calculus, called the Max/Min Theorem (or the Extreme Value Theorem) that guarantees conditions under which you'll have both a max and a min. Calculus is so wonderful!