Finding the Domain and Range of a Function
Read Domain and Range of a Function from the Algebra I curriculum for a basic introduction to domain and range.
Finding the Domain of a Function from a Formula
The following situations are not allowed, so you must exclude value(s) that cause:
- Division by zero
- Even roots of negative numbers
- Zero raised to the zero power
Example: Find the Domain of $\,g(x) = \frac{\sqrt{x-3}}{x-5}$
SOLUTION:
$$ \begin{gather} \cssId{s11}{x-3\not\lt 0\ \text{ and }\ x-5\ne 0}\cr\cr \cssId{s12}{x-3\ge 0 \ \text{ and }\ x-5\ne 0}\cr\cr \cssId{s13}{x\ge 3\ \text{ and }\ x\ne 5}\cr\cr \cssId{s14}{\text{dom}(g) = [3,5) \cup (5,\infty)} \end{gather} $$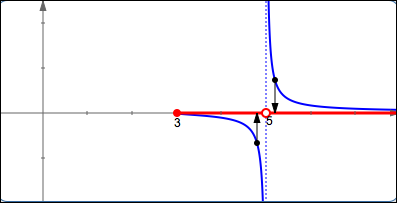
Finding the Domain of a Function from a Graph
‘Collapse’ each point into its $x$-value.
Finding the Range of a Function
The range of a function is its output set. It's easiest to find the range when you have the graph of the function. ‘Collapse’ each point into its $y$-value.
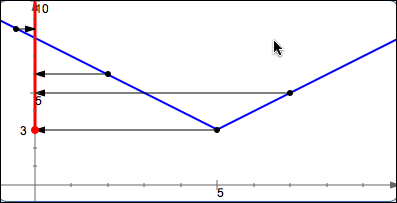
Example: Find the Range of $\,f(x) = |x-5| + 3$
SOLUTION: Graph $\,f\,$ by starting with $\,y = |x|\,,$ shifting it right $\,5\,$ and up $\,3\,.$
$$ \cssId{s27}{\text{ran}(f) = [3,\infty)} $$