audio read-through The Natural Exponential Function

Recall that by definition, an exponential function is of the form $\,f(x) = b^x\,,$ where $\,b\,$ is a positive number not equal to $\,1\,.$

Inside the class of exponential functions (one member for each allowable value of the base $\,b\,$) there is a particular member that is singled out as being most important.

Why? It has a simple property (discussed in a future section) that usually makes it easier to work with than any other member of its class.

This special member has base $\,\text{e}\,,$ and is called the natural exponential function. The natural exponential function is so important that if you hear someone say ‘the exponential function’ (as opposed to ‘an exponential function’), then they're talking about $\,f(x) = \text{e}^x\,.$

This most important member of its class is shown in red below:

Click the Button to See

of the Class of Exponential Functions

The Irrational Number $\,\text{e}\,$

It might be curious to you that the proclaimed ‘simplest’ exponential function has such an ‘unusual’ base. You might wonder—shouldn't a simple base like $\,2\,$ or $\,3\,$ be better? So, let's begin by studying this special base—the irrational number $\,\text{e}\,.$

A Review of Irrational Numbers

An Important Expression:  $\left(1 + \frac 1n\right)^n$

There's a definition of the irrational number $\,\text{e}\,$ that is particularly important in our context. This definition involves looking at the expression $\left(1 + \frac 1n\right)^n$ for large positive values of $\,n\,.$ An exploration of this expression is also a good example of where intuition can fail you in mathematics!

Consider the expression $\,\left( 1 + \frac 1n\right)^n\,$ for bigger and bigger positive integer values of $\,n\,.$ When I ask students what number they think this ‘looks like’ for such values of $\,n\,,$ I often get the answer ‘$\,1\,$’.

The (flawed) reasoning goes something like this:

Let's take a look at what is really happening, and discuss the flaw in the previous ‘argument’. The table below lists some values:

$n$ $\displaystyle\left(1 + \frac 1n\right)^n$
$10$$\displaystyle\left(1 + \frac 1{10}\right)^{10} \approx 2.5937$
$100$$\displaystyle\left(1 + \frac 1{100}\right)^{100} \approx 2.7048$
$1000$$\displaystyle\left(1 + \frac 1{1000}\right)^{1000} \approx 2.7169$
$10,000$$\displaystyle\left(1 + \frac 1{10,000}\right)^{10,000} \approx 2.7181$
$\downarrow$$\downarrow$
$\infty$$\text{e}$

Clearly, the numbers in the right-hand column above are not approaching the number $\,1\,.$ They are, however, approaching a particular number: this is precisely the number that we call $\,\text{e}\,.$

DEFINITION the number $\,\text{e}\,$

The number  $\,\text{e}\,$  is the limit, as $\,n\,$ goes to infinity, of $\,\left(1 + \frac 1n\right)^n\,.$

More compactly:

$$ \cssId{s59}{\text{e} = \lim_{n\rightarrow\infty} \left(1 + \frac 1n\right)^n} $$

We can get the numbers $\,\left(1 + \frac 1n\right)^n\,$ as close to $\,\text{e}\,$ as desired, by making $\,n\,$ sufficiently large.

The Flaw in the Prior Argument

In the prior argument, we let the value of $\,n\,$ inside the parentheses go to infinity first, and then we let the exponent go to infinity. However, when evaluating limits, you must let every occurrence of $\,n\,$ go to infinity at the same time!

The Graph of the Natural Exponential Function

Here are graphs of the natural exponential function, together with two nearby functions:

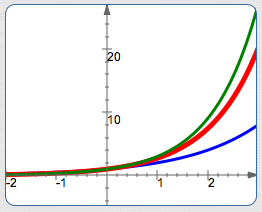
the natural exponential function and neighbors

For $\,x \gt 0\,,$  $\,\color{blue}{2^x} \lt \color{red}{{\text{e}}^x} \lt \color{green}{3^x}\,$

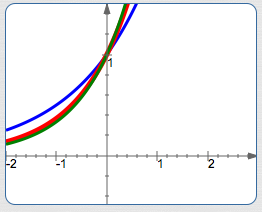
the natural exponential function and neighbors

For $\,x \lt 0\,,$  $\,\color{green}{3^x} \lt \color{red}{{\text{e}}^x} \lt \color{blue}{2^x}\,$

Concept Practice