The Complex Conjugate

This section continues the discussion of complex numbers that was begun with:

Much of the material on this current page is needed to prove a beautiful property of polynomials with real number coefficients: any non-real zeroes must occur in complex conjugate pairs.

(More on this in a future section!)

THE COMPLEX CONJUGATE definition, notation, properties

Let $\,a\,$ and $\,b\,$ be real numbers, and let $\,i:=\sqrt{-1}\,$.
Recall that:

the real part of $\,a+bi\,$ is: $\,a\,$
the imaginary part of $\,a+bi\,$ is: $\,b\,$

For example, the complex number $\,3 + 2i\,$ has real part $\,3\,$ and imaginary part $\,2\,$.

DEFINITION: COMPLEX CONJUGATE
The complex conjugate of $\,a + bi\,$ is $\,a - bi\,$.
Thus, to find the complex conjugate:
- keep the real part the same
- take the opposite of the imaginary part
In context, you can use the single word ‘conjugate’
instead of the two-word ‘complex conjugate’.
For example:
the conjugate of $\,3+2i\,$ is $\,3 - 2i\,$;
the conjugate of $\,3 - 2i\,$ is $\,3 + 2i\,$.
NOTATION FOR THE COMPLEX CONJUGATE:
The complex conjugate of $\,z\,$ is denoted by $\,\overline{z}\,$ and read aloud as ‘$\,z\,$ bar’.
Thus, if $\,z := a + bi\,$, then we have $\,\overline z = \overline{a + bi} = a - bi\,$.
For example, $\,\overline{3 + 2i} = 3 - 2i\,$ and $\,\overline{3 - 2i} = 3 + 2i\,$.
COMPLEX CONJUGATE PAIRS:
A complex number with a nonzero imaginary part, together with its conjugate,
are called a complex conjugate pair or, more simply, a conjugate pair.
Thus, $\,a + bi\,$ and $\,a - bi\,$ are a complex conjugate pair for $\,b\ne 0\,$.

The numbers (say) $\,5 + 0i\,$ and $\,5 - 0i\,$ are complex conjugates,
but they are not a complex conjugate pair,
since they are not distinct numbers.
THE CONJUGATE OF A REAL NUMBER:
If $\,x\,$ is a real number, then $\,\overline{x} = x\,$.
That is, the complex conjugate of a real number is itself.
Proof:
$\overline{x} = \overline{x + 0i} = x - 0i = x$
THE CONJUGATE OF A SUM:
The conjugate of a sum is the sum of the conjugates.
That is, for all complex numbers $\,z\,$ and $\,w\,$: $$ \cssId{s47}{\overline{z + w} = \overline{z} + \overline{w}} $$ Proof:
Let $\,z := a + bi\,$ and $\,w := c + di\,$, where $\,a\,$, $\,b\,$, $\,c\,$ and $\,d\,$ are real numbers.
Note that $\,\overline{z} = a - bi\,$ and $\,\overline{w} = c - di\,$.
Then: $$ \begin{alignat}{2} \cssId{s53}{\overline{z + w}}\ &\cssId{s54}{= \overline{(a + bi) + (c + di)}} &&\qquad \cssId{s55}{\text{definition of $\,z\,$ and $\,w\,$}}\cr\cr &\cssId{s56}{= \overline{ (a+c) + (b+d)i}} &&\qquad \cssId{s57}{\text{addition of complex numbers}}\cr\cr &\cssId{s58}{= (a+c) - (b+d)i} &&\qquad \cssId{s59}{\text{definition of complex conjugate}}\cr\cr &\cssId{s60}{= (a - bi) + (c - di)} &&\qquad \cssId{s61}{\text{re-arrange terms}}\cr\cr &\cssId{s62}{= \overline{z} + \overline{w}} &&\qquad \cssId{s63}{\text{definition of complex conjugate}} \end{alignat} $$
THE CONJUGATE OF A PRODUCT:
The conjugate of a product is the product of the conjugates.
That is, for all complex numbers $\,z\,$ and $\,w\,$: $$ \cssId{s67}{\overline{zw} = \overline{z}\cdot\overline{w}} $$ Proof:
Let $\,z := a + bi\,$ and $\,w := c + di\,$, where $\,a\,$, $\,b\,$, $\,c\,$ and $\,d\,$ are real numbers.
Note that $\,\overline{z} = a - bi\,$ and $\,\overline{w} = c - di\,$.
Note also that $\,(a - bi)(c - di) = ac - adi -bci - bd = (ac-bd) - (bc+ad)i\,$.
Then: $$ \begin{alignat}{2} \cssId{s74}{\overline{zw}}\ &\cssId{s75}{= \overline{(a + bi)(c + di)}} &&\qquad \cssId{s76}{\text{definition of $\,z\,$ and $\,w\,$}}\cr\cr &\cssId{s77}{= \overline{ (ac-bd) + (bc + ad)i}} &&\qquad \cssId{s78}{\text{multiplication of complex numbers}}\cr\cr &\cssId{s79}{= (ac - bd) - (bc+ad)i} &&\qquad \cssId{s80}{\text{definition of complex conjugate}}\cr\cr &\cssId{s81}{= (a - bi)(c - di)} &&\qquad \cssId{s82}{\text{see the note above}}\cr\cr &\cssId{s83}{= \overline{z}\cdot\overline{w}} &&\qquad \cssId{s84}{\text{definition of complex conjugate}} \end{alignat} $$
THE CONJUGATE OF POWERS:
For integers $\,n\ge 2\,$ and for all complex numbers $\,z\ $: $$ \cssId{s87}{\overline{z^n} = {(\,\,\overline{z}\,)\,}^n} $$ Proof when $\,n = 2\,$:
Since the conjugate of a product is the product of the conjugates, $$ \cssId{s90}{\overline{z^2}} \cssId{s91}{= \overline{z\cdot z}} \cssId{s92}{= \overline{z}\cdot\overline{z}} \cssId{s93}{= {(\,\,\overline{z}\,)\,}^2} $$ The extension to higher powers is discussed next.

A complex number and its conjugate:

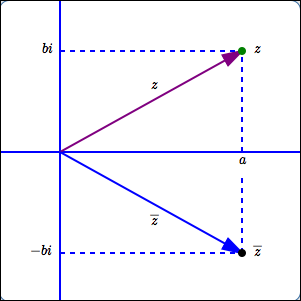
$z := a + bi$

$\overline{z} = a - bi$

A complex number $\,z\,$ can be represented:

$\bullet$ as a point

$\bullet$ as a vector from the origin to the point

The length of the vector representing $\,z\,$
is called the modulus of $\,z\,$
and is denoted by $\,|z|\,$.

Equivalently, $\,|z|\,$ represents
the distance of the complex number
from the origin in the complex plane.

From the Pythagorean Theorem:
$|z| = \sqrt{a^2 + b^2}$

Extending Properties to Finite Sums/Products

Properties that ‘look like’ they hold for only two complex numbers actually hold for any finite number of complex numbers.
The key is to take two things and treat them as a single thing, as shown next:
$$ \begin{alignat}{2} \cssId{s111}{\overline{u + v + w}} \ & \cssId{s112}{= \overline{(u + v) + w}} &&\qquad\cssId{s113}{\text{treat $\,u+v\,$ as a singleton}}\cr\cr &\cssId{s114}{= \overline{u+v} + \overline{w}} &&\qquad\cssId{s115}{\text{it works for two}}\cr\cr &\cssId{s116}{= \overline{u} + \overline{v} + \overline{w}} &&\qquad\cssId{s117}{\text{it works for two}} \end{alignat} $$ Since it works for two, it works for three.
Repeating the process—since it works for three, it works for four.
And so on!

Thus:

the conjugate of any finite sum of complex numbers is the sum of the conjugates
the conjugate of any finite product of complex numbers is the product of the conjugates
since $\,z^n\,$ is a finite product for any positive integer $\,n\,$, this ‘treat it as a singleton’ technique shows that $\,\overline{z^n} = {(\,\,\overline{z}\,)}^n\,$

An Important Property of Polynomials with Real Coefficients

A CONJUGATE PROPERTY for polynomials with real coefficients

If $\,P\,$ is a polynomial with real number coefficients, then $\,\overline{P(z)} = P(\overline z)\,$.

IDEA OF PROOF:
The ideas that make this work are illustrated with a quadratic polynomial, but it should be clear that they work for a polynomial of any degree.

Let $\,P(x) = ax^2 + bx + c\,$, where the coefficients are real numbers and $\,a\ne 0\,$.
Let $\,z\,$ be a complex number.
Then: $$ \begin{alignat}{2} \cssId{s137}{\overline{P(z)}} \ &\cssId{s138}{= \overline{az^2 + bz + c}} \qquad &&\cssId{s139}{\text{definition of $P$}}\cr\cr &\cssId{s140}{= \overline{az^2} + \overline{bz} + \overline{c}} &&\cssId{s141}{\text{the conjugate of a sum is the sum of the conjugates}}\cr\cr &\cssId{s142}{= \overline{a}\overline{z^2} + \overline{b}\overline{z} + \overline{c}} &&\cssId{s143}{\text{the conjugate of a product is the product of the conjugates}}\cr\cr &\cssId{s144}{= a\,\overline{z^2} + b\,\overline{z} + c} &&\cssId{s145}{\text{the conjugate of a real number is itself}}\cr\cr &\cssId{s146}{= a\,{\overline{z}}^2 + b\,\overline{z} + c} &&\cssId{s147}{\text{the power property for conjugates}}\cr\cr &\cssId{s148}{= P\,(\,\,\overline{z}\,)} &&\cssId{s149}{\text{function evaluation; definition of $\,P\,$}} \end{alignat} $$

Master the ideas from this section
by practicing the exercise at the bottom of this page.

When you're done practicing, move on to:
the quadratic formula revisited; the discriminant