Multi-Step Practice with all the Graphical Transformations
This lesson gives practice with all the graphical transformations:
- Shifting graphs up/down left/right
- Horizontal and vertical stretching/shrinking
- Reflecting about axes, and the absolute value transformation
Before practicing the multi-step exercises on this page, you should practice Single-step transformations, all mixed up. Jump to the exercises at the bottom, and click-click-click to check your understanding. When you're successfully answering all the question types, then you're ready for this current lesson!
Example: Graphing Using Transformations
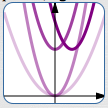
Graph $\,y = 3(x-2)^2 + 5\,$ by starting with a ‘basic model’ and successively applying graphical transformations.
(Here's the entire example in a single image! But it's too small to see easily—so keep reading ... )
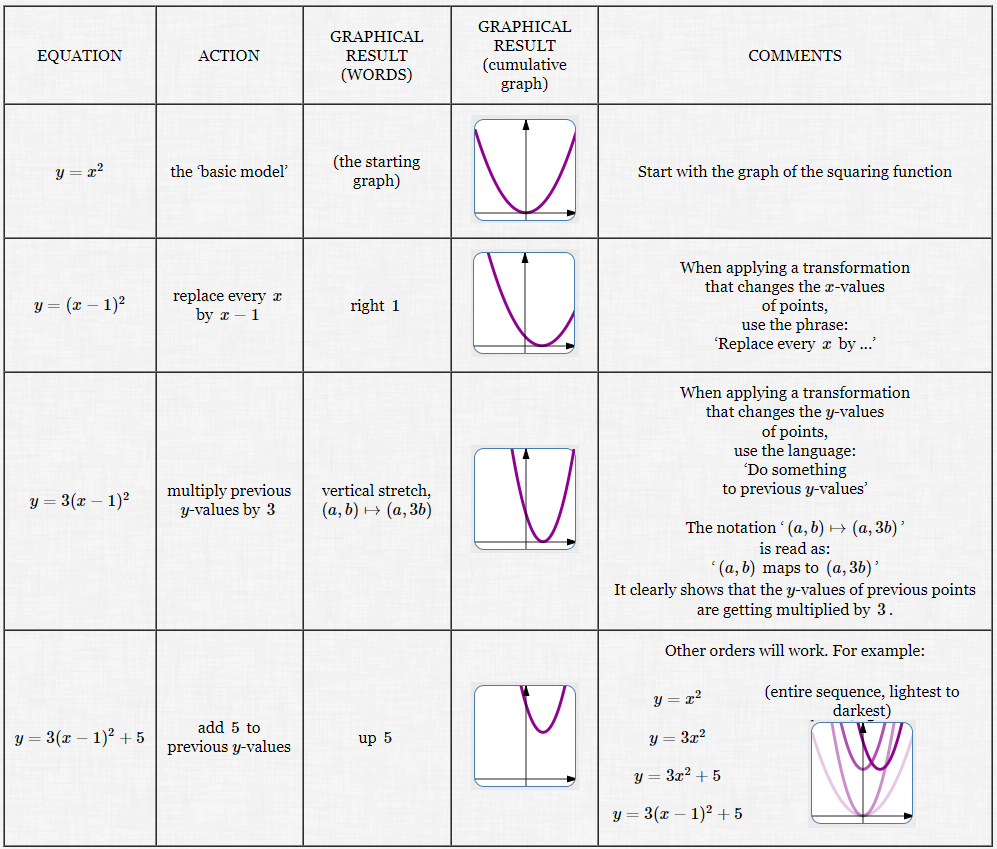
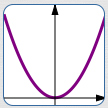
| Equation: | $y = x^2$ |
| Action: | the ‘basic model’ |
| Graphical Result (words): | (the starting graph) |
|
Graphical Result (cumulative graph): |
|
| Comments: | Start with the graph of the squaring function |
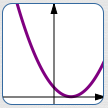
| Equation: | $y = (x-1)^2$ |
| Action: | replace every $\,x\,$ by $\,x-1\,$ |
| Graphical Result (words): | right $\,1\,$ |
|
Graphical Result (cumulative graph): |
|
| Comments: | When applying a transformation that changes the $x$-values of points, use the phrase: ‘Replace every $\,x\,$ by ...’ |
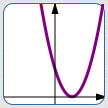
| Equation: | $y = 3(x-1)^2$ |
| Action: | multiply previous $y$-values by $\,3\,$ |
| Graphical Result (words): | vertical stretch, $\,(a,b) \mapsto (a,3b)\,$ |
|
Graphical Result (cumulative graph): |
|
| Comments: |
When applying a transformation that changes the $y$-values of points, use the language: ‘Do something to previous $y$-values’ The notation ‘$\,(a,b) \mapsto (a,3b)\,$’ is read as: ‘$\,(a,b)\,$ maps to $\,(a,3b)\,$’ It clearly shows that the $y$-values of previous points are getting multiplied by $\,3\,.$ |
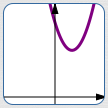
| Equation: | $y = 3(x-1)^2 + 5$ | |||||
| Action: | add $\,5\,$ to previous $y$-values | |||||
| Graphical Result (words): | up $\,5\,$ | |||||
|
Graphical Result (cumulative graph): |
|
|||||
| Comments: |
Other orders will work. For example:
|
PRACTICE: Given the Desired Graphical Results, Produce the Equations
|
Give the Equations and Actions that produce the successive desired Graphical Results. Check your answers by clicking the ‘Show Answer’ (SA) buttons. |
|||||||||
|
|||||||||
|
|||||||||
|
|||||||||
|
|||||||||
|
|||||||||
|
|||||||||
|
|||||||||