THE QUADRATIC FORMULA REVISITED; THE DISCRIMINANT

Thanks for your support!

 

REVIEW the quadratic formula, the discriminant, related concepts QUADRATIC EQUATIONS: A quadratic equation is an equation that can be written in the form $\,ax^2 + bx + c = 0\,$, where $\,a\,$, $\,b\,$ and $\,c\,$ are real numbers, with $\,a\ne 0\,$. Thus, a quadratic equation must have an $\,x^2\,$ term; it is allowed to have an $\,x\,$ term and a constant term. STANDARD FORM OF A QUADRATIC EQUATION: The form ‘$\,ax^2 + bx + c = 0\,$’ is called the standard form of the quadratic equation. Thus, in standard form, a zero appears on the right-hand side; on the left, the $\,x^2\,$ term comes first, followed by the (optional) $\,x\,$ term and the (optional) constant term. STANDARD FORM IS NOT UNIQUE: Standard form is not unique. For example, ‘$\,3x^2 - 2x + 1 = 0\,$’ and ‘$\,-3x^2 + 2x - 1 = 0\,$’ are equivalent equations; both are in standard form. If uniqueness is desired, the following additional requirements can be imposed: the greatest common factor of all nonzero coefficients is $\,1\,$ $a > 0$ THE QUADRATIC FORMULA: Let $\,a\,$, $\,b\,$ and $\,c\,$ be real numbers, with $\,a\ne 0\,$. Then, the following two equations are equivalent — they are true at the same time, and false at the same time: $$ \begin{gather} \cssId{s24}{ax^2 + bx + c = 0}\cr\cr \cssId{s25}{\color{red}{x = \frac{-b\pm\sqrt{b^2 - 4ac}}{2a}}}\cr \cssId{s26}{\color{red}{\text{THE QUADRATIC FORMULA}}} \end{gather} $$ The quadratic formula is derived here. The plus-or-minus sign ($\,\pm\,$) that appears in the quadratic formula provides a convenient shorthand. Otherwise, the quadratic formula would look like this: $$ \cssId{s30}{\color{red}{x = \frac{-b +\sqrt{b^2 - 4ac}}{2a} }} \qquad \cssId{s31}{\text{ or }} \qquad \cssId{s32}{x = \frac{-b -\sqrt{b^2 - 4ac}}{2a}} $$ The quadratic formula gives all complex solutions to the quadratic equation $\,ax^2 + bx + c = 0\,$. THE DISCRIMINANT OF A QUADRATIC EQUATION: See that expression ‘$\,b^2 - 4ac\,$’ under the square root in the quadratic formula? It is called the discriminant. As shown below, it helps us to discriminate between the various types of solutions to a quadratic equation.

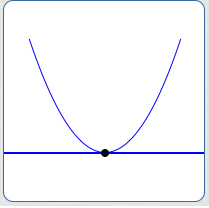
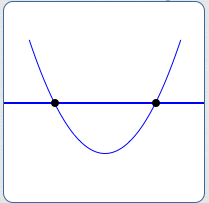
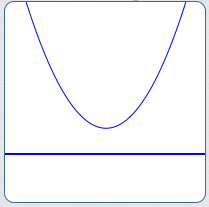
The graph of every quadratic function $\,y = ax^2 + bx + c\,$,   $\,a\ne 0\,$, is a parabola. The parabola has different $x$-intercepts based on different values of the discriminant: $b^2 - 4ac = 0$ exactly one $x$-intercept $b^2 - 4ac > 0$ two different $x$-intercepts $b^2 - 4ac < 0$ no $x$-intercepts

NATURE OF SOLUTIONS TO A QUADRATIC EQUATION WITH REAL COEFFICIENTS

There are three types of solution sets possible for a quadratic equation $\,ax^2 + bx + c = 0\,$, $\,a\ne 0\,$.
These solution sets are determined by the discriminant, $\,b^2 - 4ac\,$: whether it is zero, positive, or negative.
The three situations are summarized in the table below.

SOLUTIONS OF $ax^2 + bx + c = 0\,$,   coefficients are real numbers, $a\ne 0$
value of the discriminant	$b^2 - 4ac = 0\ $	$b^2 - 4ac > 0\ $	$b^2 - 4ac < 0\ $
nature of solution set	exactly one real number solution	two different real number solutions	no real number solutions; a complex conjugate pair
the solution(s) are:	$$\cssId{s57}{\displaystyle\,x = -\frac{b}{2a}}$$	$\displaystyle\, x = \frac{-b + \sqrt{b^2 - 4ac}}{2a}$ or $\displaystyle\,x = \frac{-b - \sqrt{b^2 - 4ac}}{2a}$	$$ \begin{align} \cssId{s66}{x\ } &\cssId{s67}{= \frac{-b + i\sqrt{-(b^2 - 4ac)}}{2a}}\cr &\cssId{s68}{= -\frac{b}{2a} + i\frac{\sqrt{-(b^2-4ac)}}{2a}} \end{align} $$ or $$ \begin{align} \cssId{s70}{x\ } &\cssId{s71}{= \frac{-b - i\sqrt{-(b^2 - 4ac)}}{2a}}\cr &\cssId{s72}{= -\frac{b}{2a} - i\frac{\sqrt{-(b^2-4ac)}}{2a}} \end{align} $$
			Note: Since $\,b^2 - 4ac < 0\,$, we have $\,-(b^2 - 4ac) > 0\,$. Therefore, $\,\frac{\sqrt{-(b^2-4ac)}}{2a} \ne 0\,$, so these two solutions have the same real part and opposite nonzero imaginary parts, hence form a complex conjugate pair.

IRREDUCIBLE QUADRATICS

The quadratic expression $\ ax^2 + bx + c\ $ ($\,a \ne 0\,$) is called irreducible if $\ b^2 - 4ac < 0\ $.

Equivalently, the quadratic expression $\ ax^2 + bx + c\ $ ($\,a \ne 0\,$) is called irreducible if the equation $\,ax^2 + bx + c = 0\,$ has no real number solutions.

In this case, the trinomial $\,ax^2 + bx + c\,$ cannot be factored using real numbers.
It can, however, be factored using the complex conjugate pair that is given by the quadratic formula.
This idea is explored in a future section.

EXAMPLES: Connection Between Zeroes and Factors

Recall the beautiful relationship between the zeroes of a polynomial and its factors:

$k\,$ is a zero             if and only if             $x-k\,$ is a factor
Indeed, the only factor that the zeroes don't give is a constant factor, which we often need to provide ourselves.
Some examples follow.

EXAMPLE:
Find a quadratic function with zeroes $\,2\,$ and $\,-3\,$;
the coefficient of the $\,x^2\,$ term should equal $\,5\,$.

SOLUTION:
Since $\,2\,$ is a zero, $\,x - 2\,$ is a factor.
Since $-3\,$ is a zero, $\,x - (-3) = x + 3\,$ is a factor.
Since the coefficient of the $\,x^2\,$ term must be $\,5\,$, we need a constant factor of $\,5\,$.
(Note that this constant factor does not change the zeroes.)

The function $\,f\,$ defined below is the desired quadratic function: $$\, \cssId{s103}{f(x)} \cssId{s104}{= 5(x-2)(x+3)} \cssId{s105}{= \ldots} \cssId{s106}{= 5x^2 + 5x - 30} \,$$

EXAMPLE:
Find a quadratic function with real coefficients that has exactly one real zero, $x = 4\,$.
The coefficient of the $\,x\,$ term should equal $\,7\,$.

SOLUTION:
Since $\,4\,$ is a zero, $\,x - 4\,$ is a factor.
To get a quadratic function with no different zero, we need two factors of $\,x - 4\,$.
Thus, every function of the form $\,k(x-4)(x-4) = \ldots = kx^2 - 8kx + 16k\,$ satisfies the zero requirement.
For the coefficient of the $\,x\,$ term to equal $\,7\,$, we need $\,-8k = 7\,$, so $k = -\frac{7}{8}\,$.

The function $\,f\,$ defined below is the desired quadratic function: $$\, \cssId{s116}{f(x)} \cssId{s117}{= -\frac{7}{8}(x-4)(x-4)} \cssId{s118}{= \ldots} \cssId{s119}{= -\frac{7}{8}x^2 + 7x - 14}\,$$

Master the ideas from this section
by practicing the exercise at the bottom of this page.

When you're done practicing, move on to:
multiplicity of zeros: graphical consequences