Graphing Generalized Sines and Cosines, Like $\,y = a\sin k(x\pm b)\,$ and $\,y = a\cos (kx\pm B)\,$ (Part 2)

(This page is Part 2. Click here for Part 1.)

Examples

The three earlier examples are repeated, using a compact version of the four-step graphing process. A new example is also given. See how quick and easy it is!

In these examples, cycles are shown in a standard viewing window ($\,x\,$ between $\,-20\,$ and $\,20\,$; $\,y\,$ between $\,-10\,$ and $\,10\,$), to make comparisons between graphs easier.

The cycle being graphed with the four-step process is shown in dark green. Additional cycles are shown to complete the viewing window.

Decimal approximations to the tenths place are included. Remember to get exact answers first, then approximate!

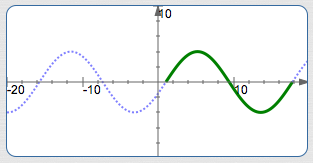
Graph $\,y = -1.5\sin\frac12(x-\pi)\,$ Using the Four-Step Process

1. $k = \frac 12 = 0.5$

2. $S = \pi \approx 3.1$

   (Mentally set $\,\frac 12(x-\pi)\,$ equal to zero)

3. $\displaystyle\text{Period} = \frac{2\pi}{k} = \frac{2\pi}{0.5} = 4\pi \approx 12.6 $

   $E = S + \text{period} = \pi + 4\pi = 5\pi \approx 15.7$

4. Basic sine cycle, flipped, on about $\,[3.1,15.7]\,,$ amplitude is $\,1.5\,$:

   

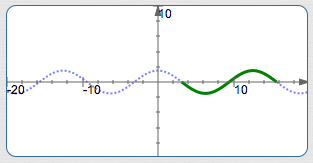
Graph $\,y = \frac13\cos (4x+5)\,$ Using the Four-Step Process

1. $k = 4$

2. $S = -\frac{5}{4} = -1.25$

   (Mentally set $\,4x+5\,$ equal to zero)

3. $\displaystyle\text{Period} = \frac{2\pi}{k} = \frac{2\pi}{4} = \frac{\pi}{2} \approx 1.6$

   $\displaystyle\displaystyle E = S + \text{period} = -1.25 + \frac{\pi}2 \approx 0.3$

4. Basic cosine cycle on (about) $\,[-1.25,0.3]\,,$ amplitude is $\displaystyle\,\frac{1}{3}\,$:

   

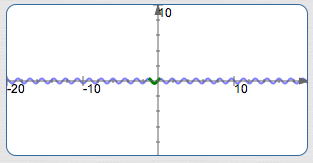
Graph $\,y = -7\cos (3 - 5x)\,$ Using the Four-Step Process

1. Rewrite:

   $$ \begin{align} -7\cos(3-5x) &= -7\cos(-(5x-3))\cr &= -7\cos(5x-3) \end{align} $$

   (Cosine is even)

   $k = 5$

2. $S = \frac{3}{5} = 0.6$

   (Mentally set $\,5x-3\,$ equal to zero)

3. $\displaystyle\text{Period} = \frac{2\pi}{5} = 0.4\pi \approx 1.3 $

   $E = S + \text{period} = 0.6 + 0.4\pi \approx 1.9$

4. Basic cosine cycle, flipped, on about $\,[0.6,1.9]\,,$ amplitude is $\,7\,$:

   

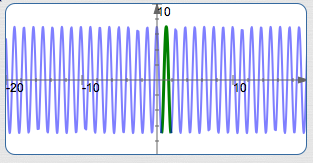
Graph $\displaystyle\,y = -4\sin\frac{\pi-3x}{8} \,$ Using the Four-Step Process

1. Rewrite:

   $$\begin{align} -4\sin\frac{\pi-3x}{8} &= -4\sin (-\frac 18(3x-\pi))\cr &= 4\sin\frac18(3x - \pi) \end{align} $$

   (Sine is odd)

   $\displaystyle k = \frac38 \approx 0.4$

2. $\displaystyle S = \frac{\pi}{3} \approx 1.0$

   (Mentally set $\displaystyle\,\frac18(3x-\pi)\,$ equal to zero)

3. $\displaystyle\text{Period} = \frac{2\pi}{3/8} = \frac{16\pi}3 \approx 16.8 $

   $\displaystyle E = S + \text{period} = \frac{\pi}3 + \frac{16\pi}3 = \frac{17\pi}3 \approx 17.8$

4. Basic sine cycle on about $\,[1.0,17.8]\,,$ amplitude is $\,4\,$: