‘TRAPPING’ THE ROOTS OF A POLYNOMIAL;
AN INTERVAL GUARANTEED TO CONTAIN ALL REAL ROOTS

Thanks for your support!

 

 

Notes on the theorem

• recall that ‘:=’ means ‘equals, by definition’
• to find $\,M\,$:   look at all the coefficients except the leading coefficient,
  and choose the one with the biggest absolute value
• For more advanced readers:
  • You may want to compare the theorem and proof on this page with Cauchy's Bound for the Roots of a Polynomial.
  • The theorem and proof given on this page provides a bound for all complex roots of a polynomial.
    In this case, $\,K\,$ is the radius of a bounding circle centered at the origin in the complex plane.
    For a complex number $\,z\,,$ $\,|z|\,$ is called the modulus of $\,z\,.$
    $$\, \cssId{s35}{|z|} \ \cssId{s36}{=\ |a + bi|}\ \cssId{s37}{=\ \text{distance of $\,z\,$ from the origin in the complex plane}} \ \cssId{s38}{=\ \sqrt{a^2 + b^2}}$$
  • The theorem and proof given on this page work when the polynomial coefficients $\,a_i\,$ are complex numbers.

 

EXAMPLES—HOW TO USE THE THEOREM

Example 1

Let $\,P(x) = (x-1)(x+2)(x-3) = x^3 - 2x^2 - 5x + 6\,.$

It's clear from the factored form that the roots of $\,P\,$ are $\,1\,,$ $\,-2\,,$ and $\,3\,,$
so we'll be able to confirm the bounding interval obtained from the theorem.

$n\,$ (the degree) is $3$

$a_3\,$ (the leading coefficient) is $\,1\,$

$M = \text{max}\bigl(\,|-2|\,,\,|-5|\,,\,|6|\,\bigr) = 6$

$\displaystyle K \ =\ 1 + \frac{M}{|a_n|} \ =\ 1 + \frac{6}{|1|} \ =\ 1 + 6 = 7$

All the zeroes are guaranteed to lie in the interval $\,[-K,K] = [-7,7]\,$ (which they do!)

Example 2

The previous example is tweaked by changing the leading coefficient to $\,7\,.$

Let $\,P(x) = 7x^3 - 2x^2 - 5x + 6\,.$

$n\,$ (the degree) is $3$

$a_3\,$ (the leading coefficient) is $\,7\,$

$M = \text{max}\bigl(\,|-2|\,,\,|-5|\,,\,|6|\,\bigr) = 6$

$\displaystyle K \ =\ 1 + \frac{M}{|a_n|} \ =\ 1 + \frac{6}{|7|} \ =\ \frac{13}{7}\ \approx\ 1.9$

All the zeroes are guaranteed to lie in the interval $\,[-\frac{13}{7},\frac{13}{7}]\,.$

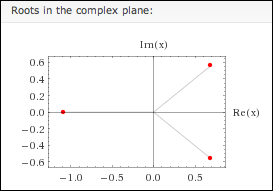
A quick trip to WolframAlpha shows that there is only one real root, which is approximately $\,-1.1\,.$
Here's a sketch from WolframAlpha that shows all the complex roots:

 

TOOLS NEEDED TO PROVE THE THEOREM

1. THE TRIANGLE INEQUALITY:
   For all real numbers $\,a\,$ and $\,b\,$:   $|a+b| \le |a| + |b|$
2. PROPERTIES OF ABSOLUTE VALUE:
   For all real numbers $\,a\,$ and $\,b\,$:
   • $|ab| = |a|\cdot|b|$
   • $\displaystyle \left|\frac{a}{b}\right| = \frac{|a|}{|b|}$     ($b\ne 0$)
3. Properties (1) and (2) extend to finite sums/products.
   For example:
   $|a + b + c| \le |a| + |b + c| \le |a| + |b| + |c|$
   and
   $|abc| = |a|\cdot|bc| = |a|\cdot|b|\cdot|c|$
   
   In particular: $|x^n| = |x|^n$
4. Properties (1) and (2) also hold for complex numbers, where $\,|\cdot|\,$ is the modulus of a complex number.
   Complex numbers are explored in the next few sections.
5. SUM OF A FINITE GEOMETRIC SERIES:
   For all real numbers $\,a\,$ and $\,x\,$:
   $\displaystyle a + ax + ax^2 + \cdots + ax^n = \frac{a(x^{n+1}-1)}{x-1}$

 

PROOF OF THE BOUNDING THE REAL ROOTS OF A POLYNOMIAL THEOREM

Let $\,r\,$ be a real root of $\,P\,,$ so $\,P(r) = 0\ $: $$\cssId{sb2}{a_nr^n + a_{n-1}r^{n-1} + \cdots + a_1r + a_0 = 0}$$ Dividing both sides of the equation by $\,a_n\ne 0\,$ gives the equivalent equation: $$\cssId{sb4}{r^n + \frac{a_{n-1}}{a_n}r^{n-1} + \cdots + \frac{a_1}{a_n}r + \frac{a_0}{a_n} = 0} \tag{1}$$

Define $\displaystyle\,M := \text{max}\bigl(\,|a_{n-1}|,\ldots,|a_0|\,\bigr)\,,$ so that $$ \cssId{sb6}{\text{max}\left(\left|\frac{a_{n-1}}{a_n}\right|,\ldots,\left|\frac{a_0}{a_n}\right|\right)} \cssId{sb7}{= \text{max}\left(\frac{|a_{n-1}|}{|a_n|},\ldots,\frac{|a_0|}{|a_n|}\right)} \cssId{sb8}{= \frac{\text{max}(|a_{n-1}|,\ldots,|a_0|)}{|a_n|}} \cssId{sb9}{= \frac{M}{|a_n|}} $$

We consider two cases: $|r|\le 1\,$ and $|r| > 1\,.$   In both cases, it must be shown that $\displaystyle\,|r| \le 1 + \frac{M}{|a_n|}\,.$

$|r| \le 1$

Assume $\,|r| \le 1\,.$ Since absolute value is a nonnegative quantity, $\displaystyle\,\frac{M}{|a_n|} \ge 0\,.$
Then, as desired, we have: $$\cssId{sb17}{|r| \quad\le\quad 1 \quad\le\quad 1 + \frac{M}{|a_n|}}$$

$|r| > 1$

Assume $|r| > 1$. Rewrite (1) as $$\cssId{sb20}{r^n = -\frac{a_0}{a_n} - \frac{a_1}{a_n}r - \cdots - \frac{a_{n-1}}{a_n}r^{n-1}}\tag{2}$$ Then: $$ \begin{alignat}{2} \cssId{sb22}{|r^n|} \quad &\cssId{sb23}{= \quad \left|-\frac{a_0}{a_n} - \frac{a_1}{a_n}r - \cdots - \frac{a_{n-1}}{a_n}r^{n-1}\right|} &&\cr\cr &\cssId{sb24}{\le \quad \left|\frac{a_0}{a_n}\right| + \left|\frac{a_1}{a_n}r\right| + \cdots + \left|\frac{a_{n-1}}{a_n}r^{n-1}\right|} &\qquad\qquad&\cssId{sb25}{\text{triangle inequality}}\cr\cr &\cssId{sb26}{= \quad \frac{|a_0|}{|a_n|} + \frac{|a_1|}{|a_n|}|r| + \cdots + \frac{|a_{n-1}|}{|a_n|}|r^{n-1}|} &\qquad\qquad& \cssId{sb27}{\text{since} \left|\frac{a}{b}\right| = \frac{|a|}{|b|} \text{ and } |ab| = |a|\cdot|b|}\cr\cr &\cssId{sb28}{= \quad \frac{1}{|a_n|}\left(|a_0| + |a_1|\cdot|r| + \cdots + |a_{n-1}|\cdot|r^{n-1}|\right)} &&\cssId{sb29}{\text{factor out the common factor}} \cr\cr &\cssId{sb30}{\le \quad \frac{1}{|a_n|}\left(M + M|r| + \cdots + M|r^{n-1}|\right)} &&\cssId{sb31}{\text{since $M$ is the max}}\cr\cr &\cssId{sb32}{\le \quad \frac{1}{|a_n|}\left(M + M|r| + \cdots + M|r|^{n-1}\right)} &&\cssId{sb33}{\text{since $|r^i| = |r|^i$}}\cr\cr &\cssId{sb34}{= \quad \frac{M}{|a_n|}(1 + |r| + \cdots + |r|^{n-1})} &&\cssId{sb35}{\text{factor out $M$}}\cr\cr &\cssId{sb36}{= \quad \frac{M}{|a_n|}\left(\frac{|r|^n-1}{|r| - 1}\right)}&&\cssId{sb37}{\text{sum the geometric series}}\cr\cr \end{alignat} $$ Thus: $$ \cssId{sb39}{|r^n| \le \frac{M}{|a_n|}\left(\frac{|r|^n-1}{|r| - 1}\right)} \tag{3} $$ Multiplying or dividing both sides of an inequality by a positive number does not change the direction of the inequality symbol.
Since, by hypothesis, $\,|r| >1\,,$ we have $\,|r| - 1 > 0\,.$
Also, $$\cssId{sb42}{|r^n|} \cssId{sb43}{= |r|^n} \cssId{sb44}{> 1^n} \cssId{sb45}{= 1} \cssId{sb46}{> 0} $$ So, dividing both sides of (3) by $|r^n| = |r|^n$ and multiplying by $\,|r| - 1\,$ gives $$ \cssId{sb48}{|r| - 1} \cssId{sb49}{\le \frac{M}{|a_n|}\frac{|r|^n - 1}{|r|^n}} \cssId{sb50}{= \frac{M}{|a_n|}\left(1 - \frac{1}{|r|^n}\right)} $$ Note:
$$ \cssId{sb52}{|r| > 1} \quad \cssId{sb53}{\Rightarrow}\quad \cssId{sb54}{|r|^n > 1} \quad \cssId{sb55}{\Rightarrow}\quad \cssId{sb56}{0 < \frac{1}{|r|^n} < 1}\quad \cssId{sb57}{\Rightarrow}\quad \cssId{sb58}{0 > -\frac{1}{|r|^n} > -1}\quad \cssId{sb59}{\overbrace{\ \ \Rightarrow\ \ }^{\text{add $1$}}}\quad \cssId{sb60}{1 > 1-\frac{1}{|r|^n} > 0}\quad \cssId{sb61}{\Rightarrow}\quad \cssId{sb62}{0 < 1-\frac{1}{|r|^n} < 1} $$ so $$\cssId{sb64}{|r| - 1 \le \frac{M}{|a_n|}}$$ from which we get the desired result that $$\cssId{sb66}{ |r| \le 1 + \frac{M}{|a_n|}}$$ QED

Master the ideas from this section
by practicing the exercise at the bottom of this page.

When you're done practicing, move on to:
introduction to complex numbers