Periodic Functions

Periodic functions exhibit repetitive behavior—as you move to the left or right on the graph, there is some ‘template’ that repeats itself, forever and ever.

This section gives a precise introduction to periodic functions.

(A)

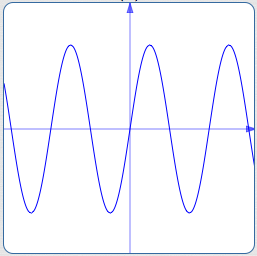
A periodic function defined for all real numbers

(B)

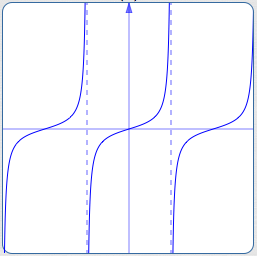
A periodic function that is not defined for all real numbers

(C)

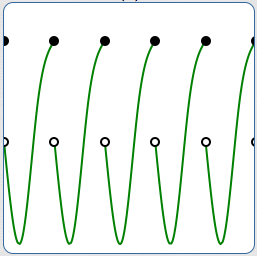
A fun periodic function

Some frequently-appearing definitions of periodic functions are a bit ‘flawed’. The definition that follows corrects the situation. See below for details.

DEFINITION periodic function; period

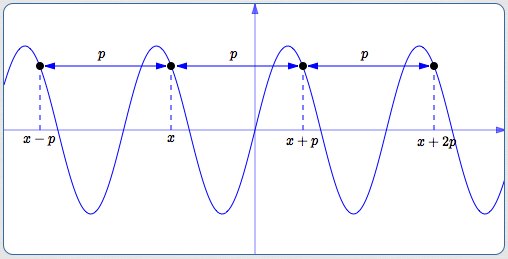
A function $\,f\,$ is periodic if and only if there exists a positive number $\,p\,$ with the following properties:

Whenever $\,x\,$ is in the domain of $\,f\,,$ so are $\,x\pm p\,$
$\,f(x + p) = f(x - p) = f(x)\,$

Such a number $\,p\,$ is called a period of the function $\,f\,.$

Notes on the Definition

Periodicity is an Existence Statement

The definition of periodic function is an existence statement. In order for a function to be periodic, there must exist a positive number, $\,p\,,$ with special properties.

What are these Special Properties?

Pick any real number $\,x\,$ in the domain of $\,f\,$; this input has corresponding output $\,f(x)\,.$
When you move $\,p\,$ to the right, the new input is $\,x + p\,.$

When you move $\,p\,$ to the left, the new input is $\,x - p\,.$

Both of these new inputs ($\,x + p\,$ and $\,x - p\,$) must also be in the domain of $\,f\,.$
The inputs $\,x + p\,$ and $\,x - p\,$ have corresponding outputs $\,f(x + p)\,$ and $\,f(x - p)\,.$
All three outputs must be equal: $$f(x) = f(x + p) = f(x - p)$$
In other words: No matter where you start on the graph, if you move $\,p\,$ units to the right or $\,p\,$ units to the left, you always arrive at a point with the same $y$-value.

Make Sure You See the ‘Domino’ Effect!

Suppose $\,f\,$ is periodic with a period $\,p\,,$ and let $\,x\,$ be in the domain of $\,f\,.$ For convenience, let $\,\text{dom}(f)\,$ be an abbreviation for the domain of $\,f\,.$

Recall that ‘$\,\Rightarrow\,$’ is a shorthand for ‘implies’.

Then:

$$ \begin{align} &\cssId{s37}{x\in\text{dom}(f)}\cr &\quad\cssId{s38}{\Rightarrow}\ \cssId{s39}{\color{red}{x+p}\in\text{dom}(f)}\cr\cr &\cssId{s40}{x+p\in\text{dom}(f)}\cr &\quad\cssId{s41}{\Rightarrow}\ \cssId{s42}{(x+p)+p = \color{red}{x + 2p}\in\text{dom}(f)}\cr\cr &\cssId{s43}{x+2p\in\text{dom}(f)}\cr &\quad\cssId{s44}{\Rightarrow}\ \cssId{s45}{(x+2p)+p = \color{red}{x + 3p}\in\text{dom}(f)} \end{align} $$

Continuing this pattern (and doing the same thing in the other direction) we see that whenever $\,x\in\text{dom}(f)\,,$ so are $\,x + kp\,$ for all integers $\,k\,.$ By the same reasoning, $\,f(x) = f(x + kp)\,$ for all integers $\,k\,.$

Periodic Functions have a ‘Template’ that can Produce the Graph

For periodic functions, you can always create a ‘template’ that produces the graph. Just keep laying it out, infinitely to the right, and infinitely to the left. The idea is illustrated below:

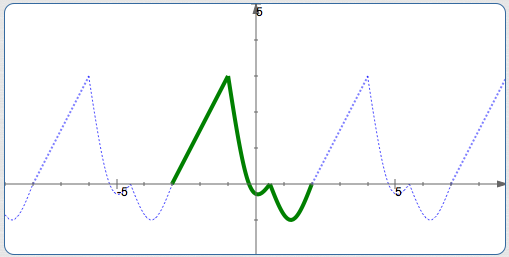
a template that produces a periodic graph

Any Template with the Same Length will Work!

Although a human eye might naturally detect a particular template for a periodic function, any template of the same length will work!

For example, the template illustrated above has length $\,5\,.$ Several other templates, each of length $\,5\,,$ are shown below. They all create exactly the same graph!

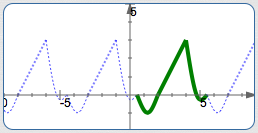
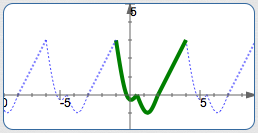
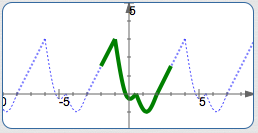
creating a periodic graph with a template

If There's One $\,p\,$ that Works, Then There are Infinitely Many!

If a template of length $\,5\,$ works, then templates of lengths $\,10\,,$ $\,15\,,$ $\,20\,$ (and so on) will also work.

In more precise terms, if a function is periodic with a period $\,p\,,$ then $\,2p\,,$ $\,3p\,,$ $\,4p\,$ (and so on) are also periods.

So, if a function has one period, then it has infinitely many. We are usually interested in the smallest period (if a smallest one exists)—this is the subject of the next section.

A Slightly Shorter Definition (But Just Not Worth It)

The definition of periodic function given in this lesson could actually be a smidgeon shorter.

As long as we require both $\,x+p\,$ and $\,x-p\,$ to be in the domain, we only need to require that $\,f(x+p) = f(x)\,.$ We get ‘$\,f(x-p) = f(x)\,$’ for free! Here's how:

Replace every $\,x\,$ in the equation ‘$\,f(x+p) = f(x)\,$’ by $\,x - p\,$:

$$ \cssId{s69}{f\bigl((x-p)+p\bigr) = f(x-p)} $$

This simplifies to:

$$ \cssId{s71}{f(x) = f(x-p)} $$

This author chose to use the slightly redundant definition because of its transparency.

Well-Intentioned Periodic Function Definitions that Don't Quite Work

A Not-General-Enough Definition, and Why

Some commonly-appearing definitions of periodic function require that the function $\,f\,$ have domain $\,\Bbb R\,.$

Such a definition doesn't need the part ‘whenever $\,x\,$ is in the domain of $\,f\,,$ so are $\,x\pm p\,$’, since $\,f\,$ knows how to act on all real numbers!

However, people using such a definition often ‘wave their hands’ and call (B) at the top of the page periodic—even though (B) doesn't even qualify, since it's not defined at each vertical asymptote.

Any reasonable person would want to call (B) periodic. The definition given in this lesson accomodates this situation.

Another Well-Intentioned Definition that Doesn't Quite Work

Some authors have recognized the need for periodic functions that aren't defined everywhere. They've tried to ‘fix’ the situation with the following definition:

A function $\,f\,$ is periodic if and only if there exists a positive number $\,p\,$ with the following properties: whenever $\,x\,$ is in the domain of $\,f\,,$ so is $\,x + p\,,$ and $\,f(x) = f(x+p)\,.$

According to this ‘one-sided’ definition, the function below would be called periodic. (Assume that the pattern indicated extends infinitely to the right, but not to the left.)

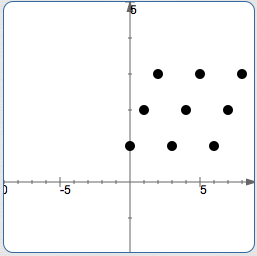
One-sided periodicity???

However, functions that people conventionally call ‘periodic’ repeat forever and ever, as you move to the right and as you move to the left.

The definition given in this lesson remedies this situation.