Compatibility of the Right Triangle and Unit Circle Approaches

There are two basic approaches to trigonometry:  the right triangle approach and the unit circle approach. Both approaches were introduced in Introduction to Trigonometry. Be sure to read this prior section, since it covers important notation and conventions.

Although at first glance the two approaches might seem totally different, they are actually beautifully intertwined: take one approach, apply a smidgeon of similar triangle theory, and the other pops out! This section shows how easy it is to go from one approach to the other.

Going From the Right Triangle Approach to the Unit Circle Approach

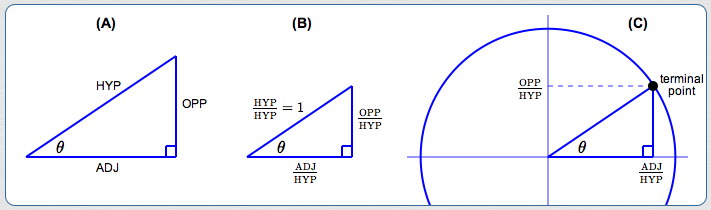
(A)  Start with an angle of interest, $\,\theta\,,$ in a right triangle.

(B)  We want to move this triangle into the unit circle, so the hypotenuse must have length $\,1\,.$ Divide all the sides by the hypotenuse. This gives a similar triangle—none of the angles change!

(C)  Move the scaled triangle into the unit circle.

What is the $x$-value of the terminal point?   Answer: $\,\frac{\text{ADJ}}{\text{HYP}}\,$

What is the $y$-value of the terminal point ?  Answer: $\,\frac{\text{OPP}}{\text{HYP}}\,$

Start with the right triangle approach, as in (A). Scale the triangle appropriately (B), and move it into the unit circle (C). Then, the unit circle approach gives:

$\cos\theta = \frac{\text{ADJ}}{\text{HYP}}$   and   $\sin\theta = \frac{\text{OPP}}{\text{HYP}}$

Going From the Unit Circle Approach to the Right Triangle Approach

(A)  Start with an angle of interest, $\,\theta\,,$ in the first quadrant of the unit circle (see below). The radius of the circle (and hence the hypotenuse of the right triangle shown) is $\,1\,.$

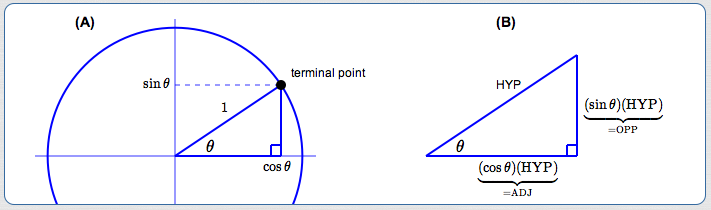
By definition:

• The $x$-value of the terminal point is $\,\cos\theta\,.$ This is also the length of the bottom of the triangle.
• The $y$-value of the terminal point is $\,\sin\theta\,.$ This is also the length of the vertical side of the triangle.

(B)  We want to turn the triangle in the circle into one with an arbitrary-length hypotenuse, ‘$\,\text{HYP}\,$’. To this end, multiply all the sides of the triangle in the circle by $\,\text{HYP}\,.$

The ADJ side now has length $\,(\cos\theta)(\text{HYP})\,.$ The OPP side now has length $\,(\sin\theta)(\text{HYP})\,.$ This gives a similar triangle—none of the angles change!

From the equation ‘$\text{ADJ} = (\cos\theta)(\text{HYP})$’ we get: $$\cssId{s41}{\cos\theta = \frac{\text{ADJ}}{\text{HYP}}}$$

From the equation ‘$\text{OPP} = (\sin\theta)(\text{HYP})$’ we get: $$\cssId{s43}{\sin\theta = \frac{\text{OPP}}{\text{HYP}}}$$

Start with the unit circle approach, as in (A). Scale the triangle in the circle to an arbitrary size (B). We get:

$\cos\theta = \frac{\text{ADJ}}{\text{HYP}}$   and   $\sin\theta = \frac{\text{OPP}}{\text{HYP}}$