Puncture Points (Holes)

Sometimes, students are fooled into thinking that a rational function has a vertical asymptote when—in reality—it has a puncture point (also called a ‘hole’).

This section provides detail and practice with punctured graphs.

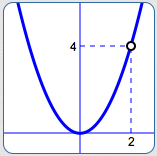
A graph with a ‘puncture point’ (also called a ‘hole’)

First, an example:

Does the function $\,R(x) = \frac{x^2 - x - 2}{x - 2}\,$ have a vertical asymptote at $\,x = 2\,$? No!

Some well-intentioned web sites conclude that this function has a vertical asymptote at $\,x = 2\,,$ simply because the denominator is zero there. This is incorrect.

In order to find a vertical asymptote, it is NOT ENOUGH to just set the denominator equal to zero.

You must ALSO check that the numerator is nonzero!

For this particular function, substitution of $\,x = 2\,$ into the numerator gives:

$$\cssId{s14}{2^2 - 2 - 2\ = \ 4 - 2 - 2 \ = \ 0}$$

Therefore, both the numerator and denominator are zero when $\,x = 2\,.$

When BOTH the numerator and denominator of a rational function are zero, then you must work harder to figure out what's going on.

You must determine what's happening CLOSE TO the $x$-value of interest.

Further analysis shows:

$$ \begin{align} \cssId{s19}{R(x)}\ &\cssId{s20}{= \frac{x^2-x-2}{x-2}}\cr\cr &\cssId{s21}{= \frac{(x+1)(x-2)}{x-2}}\cr\cr &\cssId{s22}{= (x+1)\cdot\frac{x-2}{x-2}} \end{align} $$

Cancelling off the extra factor of one:

$$\cssId{s24}{R(x) = x + 1\,,}\ \cssId{s25}{\text{providing } x\ne 2}$$

The function $\,R\,$ isn't defined when $\,x = 2\,,$ since division by zero isn't allowed.

For all values of $\,x\ne 2\,,$ ‘$\,\frac{x-2}{x-2}\,$’ is just the number $\,1\,$! The graph of $\,R\,$ is therefore the same as the line $\,y = x + 1\,,$ except that it has been ‘punctured’ at $\,x = 2\,.$

From this re-naming, it is now clear that when $\,x\,$ is close to $\,2\,,$ the outputs are close to $\,2 + 1 = 3\,.$ The graph of the function $\,R\,$ is shown below:

DEFINITION puncture points (holes)

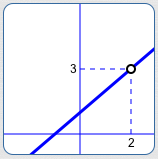
Let $\displaystyle\,R(x) = \frac{N(x)}{D(x)}\,$ be a function.

The function $\,R\,$ has a puncture point (hole) at $\,x = c\,$ if and only if the following three conditions hold:

$D(c) = 0\,$ (the denominator is zero at $\,c\,$)
$N(c) = 0\,$ (the numerator is zero at $\,c\,$)
As $\,x\,$ approaches $\,c\,,$ the values $\,R(x)\,$ approach a finite number

Notes About Puncture Points (Holes)

This Definition Holds for Rational Functions, and More!

It might be that both $\,N\,$ and $\,D\,$ are polynomials, making this a rational function (i.e., a ratio of polynomials). However, $\,N\,$ and $\,D\,$ could be more general functions.

For example, a bit of calculus shows that the function $\displaystyle\,R(x) = \frac{{\text{e}}^{x-2} - 1}{x - 2}\,$ has a hole at $\,x = 2\,.$

Note: In calculus, a ‘hole’ is an example of a removable discontinuity.

You Need All Three Conditions

It it not enough merely to require that both the numerator and denominator are zero.

Why? Instead of a puncture point, you might have a vertical asymptote.

For example, the function $$R(x) = \frac{x-2}{x^2 - 4x + 4} = \frac{x-2}{(x-2)(x-2)}$$ has a vertical asymptote at $\,x = 2\,.$

Why? For all $\,x\ne 2\,,$ $\displaystyle\,R(x) = \frac{1}{x-2}\,.$

Typical Approach for Analyzing a Rational Function for Vertical Asymptotes/Holes

Set the denominator equal to zero.
Check the resulting value(s) in the numerator.
If the denominator is zero and the numerator is nonzero, then you're guaranteed to have a vertical asymptote.
If the numerator and denominator are both zero, then you must do some additional analysis: you have either a vertical asymptote or a hole.