Introduction to Complex Numbers

Complex numbers were introduced in a prior lesson: Complex Numbers
Quickly read through this earlier lesson and do plenty of the online exercises to make sure that you understand all the concepts there.

Knowledge of the complex numbers is needed to fully understand the Fundamental Theorem of Algebra in an upcoming lesson.

For your convenience, this current lesson gives an in-a-nutshell review of complex numbers and related concepts.

REVIEW complex numbers and related concepts

By definition, the complex numbers are numbers of the form $\,a + bi\,,$
where $\,a\,$ and $\,b\,$ are real numbers, and $\,i = \sqrt{-1}\,.$

The number $\,a\,$ is called the real part of the complex number.
The number $\,b\,$ is called the imaginary part of the complex number.
Note that $\,i^2 = -1\,.$
The number $\,i\,$ is not a real number, since there is no real number which,
when squared, equals $\,-1\,.$
The solutions to $\ x^2 = -1\ $ are $\,\pm i\,$:
- when $\,x = i\,$: $\,i^2 = -1\,$
- when $\,x = -i\,$: $\,(-i)^2 = i^2 = -1\,$
a (pure) imaginary number has real part equal to $\,0\,$: e.g., $\,0 + 7i = 7i\,$
a real number has imaginary part equal to $\,0\,$: e.g., $\,5 + 0i = 5\,$
The complex numbers are graphed in a coordinate plane where:
- the real numbers lie along the horizontal axis; this is called the real axis
- the scalar multiples of $\,i\,$ lie along the vertical axis; this is called the imaginary axis
- the intersection of the real and imaginary axes is called the origin
In this scheme, the complex number $\,a + bi\,$ is found as follows:
- put a vertical line through the real number $\,a\,$ on the horizontal axis
- put a horizontal line through the imaginary number $\,bi\,$ on the vertical axis
- the number $\,a + bi\,$ is the unique intersection point of these two lines
This plane is a perfect representation of the complex numbers,
and is called the complex plane:
- every complex number corresponds to a unique point in this plane
- every point in this plane corresponds to a unique complex number
equality of complex numbers: For all real numbers $\,a\,,$ $\,b\,,$ $\,c\,$ and $\,d\,,$ $$ \cssId{s37}{a+bi=c+di}\ \ \ \ \ \cssId{s38}{\text{if and only if}}\ \ \ \ \ \cssId{s39}{(a=c\ \text{and}\ b = d)}$$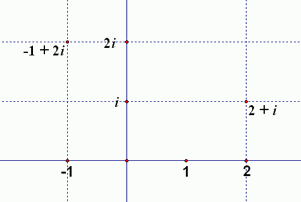

Arithmetic with complex numbers is covered in the next section.

a piece of the complex plane,
showing the numbers $\,2 + i\,$ and $\,-1 + 2i\,$

Master the ideas from this section
by practicing the exercise at the bottom of this page.

When you're done practicing, move on to:
arithmetic with complex numbers

INTRODUCTION TO COMPLEX NUMBERS