Length of a Circular Arc (and Related Concepts)

The prior section, Review of Circles (and Related Concepts), reviews definitions: circle, radius, diameter, circumference, the irrational number pi, central angles.

This section covers:

Length of a Circular Arc: The Idea
Notation Used for Arc Length
Length of a Circular Arc: Using Degree Measure for the Central Angle
Length of a Circular Arc: Using Radian Measure for the Central Angle
Why the Name ‘Radian Measure’?

Length of a Circular Arc: The Idea

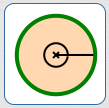
Let $\,c\,$ denote the circumference of a circle. Note: circumference is arc length with a central angle of $\,360^\circ\,.$

Computing arc length is simple: find the desired fraction ($\frac{\text{part}}{\text{whole}}$) of the circumference!

Central angles are used to determine the desired fraction. Be sure to use the same angle units for the ‘part’ and the ‘whole’, so that units cancel (as needed).

Here are examples:

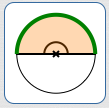arc length corresponding to 180deg central angle

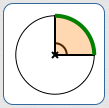$$ \begin{align} &\cssId{s16}{\text{The length of an arc with central angle $\,180^\circ\,$}}\cr &\qquad \cssId{s17}{= \overbrace{\frac{180^\circ}{360^\circ}}^{\text{part over whole}}\cdot\ c}\cr\cr &\qquad\ \ \cssId{s18}{= \frac{180}{360}\cdot c \qquad \text{(units cancel)}}\cr\cr &\qquad\ \ \cssId{s19}{= \frac{1}{2}c} \end{align} $$ arc length corresponding to 90deg central angle

arc length corresponding to 90deg central angle

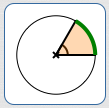$$ \begin{align} &\cssId{s20}{\text{The length of an arc with central angle $\,90^\circ\,$}}\cr\cr &\qquad\cssId{s21}{= \frac{90^\circ}{360^\circ}\cdot c}\cr\cr &\qquad\cssId{s22}{= \frac{1}{4}c} \end{align} $$ arc length corresponding to 60deg central angle

arc length corresponding to 60deg central angle

$$ \begin{align} &\cssId{s23}{\text{The length of an arc with central angle $\,60^\circ\,$}}\cr\cr &\qquad\cssId{s24}{= \frac{60^\circ}{360^\circ}\cdot c}\cr\cr &\qquad\cssId{s25}{= \frac{1}{6}c} \end{align} $$

$360^\circ\,$ central angle
$\text{arc length} = \text{circumference} = c$

$180^\circ\,$ central angle
$\text{arc length} = \frac{180^\circ}{360^\circ}\cdot c = \frac{1}{2}c$

$90^\circ\,$ central angle
$\text{arc length} = \frac{90^\circ}{360^\circ}\cdot c = \frac{1}{4}c$

$60^\circ\,$ central angle
$\text{arc length} = \frac{60^\circ}{360^\circ}\cdot c = \frac{1}{6}c$

Arc length is a desired fraction of the circumference:

$$ \begin{align} &\cssId{s35}{\text{Arc Length}}\cr\cr &\qquad \cssId{s36}{= (\text{desired fraction})(\text{circumference})}\cr\cr &\qquad \cssId{s37}{= \left(\frac{\ \ \small\displaylines{\text{central angle}\\ \text{corresponding to}\\ \text{ desired arc length}}\ \ }{\small\displaylines{\text{central angle}\\ \text{corresponding to}\\ \text{circumference}}}\right)(\text{circumference})}\cr\cr \end{align} $$

Notation Used for Arc Length

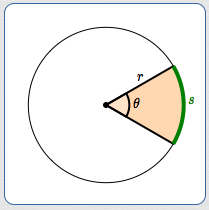
Define $\,r\,,$ $\,\theta\,,$ and $\,s\,$ as shown above:

$r\,$ is the radius of a circle
$\theta\,$ is the measure of a central angle
$s\,$ is the corresponding arc length on the circle

The angle $\,\theta\,$ can be in degrees or radians, providing you use the correct formula. Keep reading!

The units for $\,r\,$ and $\,s\,$ are (the same) length unit: e.g., feet, meters, miles, centimeters. For example, if $\,r\,$ is given in (say) feet, then a computed value for $\,s\,$ will also be feet. Or, if $\,s\,$ is given in (say) centimeters, then a computed value for $\,r\,$ will also be centimeters.

Length of a Circular Arc: Using Degree Measure

In degree measure, one complete revolution is $\,360^\circ\,.$

The circumference of a circle with radius $\,r\,$ is $\,2\pi r\,.$ Circumference takes the unit of $\,r\,,$ since the real number $\,2\pi\,$ has no units.

Let $\,\theta\,$ be a real number, without units, that represents the degree measure of a central angle. For example, if $\,\theta = 60\,,$ then $\,\theta^{\,\circ} = 60^\circ\,.$

The arc length corresponding to $\,\theta\,$ is computed as follows:

$$ \begin{align} \cssId{s55}{s}\ &\cssId{s56}{= \left(\frac{\ \ \small\displaylines{\text{central angle}\\ \text{corresponding to}\\ \text{ desired arc length}}\ \ }{\small\displaylines{\text{central angle}\\ \text{corresponding to}\\ \text{circumference}}}\right)(\text{circumference})}\cr\cr &\cssId{s57}{= \frac{\theta ^{\,\circ}}{360^\circ}(2\pi r)}\cr \end{align} $$

It may be easiest to remember the formula in one of these forms,

$$ \cssId{s59}{s = \frac{\theta^{\,\circ}}{360^\circ}(2\pi r)}\quad \cssId{s60}{\text{or}} \quad \cssId{s61}{s = \frac{\theta}{360}(2\pi r)}\,, $$

since they emphasize that arc length is just a desired fraction of the circumference. However, the formula can be simplified:

$$ \begin{align} \cssId{s64}{s}\ &\cssId{s65}{= \frac{\theta^{\,\circ}}{360^\circ}(2\pi r)}\cr\cr & \cssId{s66}{= \frac{\theta}{360}(2\pi r) \qquad \text{(the degree units cancel)}}\cr\cr & \cssId{s67}{= \frac{\theta}{180}\cdot \pi r} \end{align} $$

Thus, a simplified formula for arc length is:

$$ \cssId{s69}{s = \frac{\pi r\theta}{180}} $$

Equivalently, we can use a proportion:

$$ \begin{gather} \cssId{s71}{\frac{\text{part angle}}{\text{whole angle}} = \frac{\text{part arc length}}{\text{whole arc length}}}\cr\cr \cssId{s72}{\frac{\theta^{\,\circ}}{360^\circ} = \frac{s}{2\pi r}}\cr\cr \end{gather} $$

Cancel the degree units on the left, and then cross-multiply and solve for $\,s\,$:

$$ \begin{gather} \cssId{s74}{2\pi r\theta = 360s}\cr\cr \cssId{s75}{s = \frac{2\pi r\theta}{360}}\cr\cr \cssId{s76}{s = \frac{\pi r\theta}{180}} \end{gather} $$

Summary: Arc Length Formula when Central Angle is Measured in Degrees

There is a subtle but annoying issue that arises in the arc length formula using degree measure, as follows.

Say you want the arc length corresponding to a central angle of $\,60^\circ\,.$ You want to use the variable $\,\theta\,$ to ‘hold’ this central angle information.

You have two choices:

Let $\,\theta\,$ hold both the size and the unit: i.e., let $\,\theta = 60^\circ\,.$
Let $\,\theta\,$ hold only the (real number) size: i.e., let $\,\theta = 60\,,$ in which case $\,\theta^{\,\circ} = 60^\circ\,.$

Both ways will work, but they give rise to slightly-different-looking formulas.

Above, choice (2) was used, yielding the formula:

$$ \cssId{s88}{s = \frac{\pi r\theta}{180}} $$

For choice (1), the degree units can't be cancelled, since the unit is ‘trapped’ inside the variable $\,\theta\,.$ In this case, the formula becomes:

$$ \cssId{s91}{s = \frac{\pi r\theta}{180^\circ}} $$

Of course, when you put

$\,\theta = 60\,$ into the formula $\displaystyle s = \frac{\pi r\theta}{180}$
$\,\theta = 60^\circ\,$ into the formula $\displaystyle s = \frac{\pi r\theta}{180^\circ}$

you get precisely the same result! Make your choice, and use the appropriate formula!

Length of a Circular Arc: Using Radian Measure

In radian measure, one complete revolution is $\,2\pi\,.$

Recall that the radian measure of an angle is a real number. Radian measure has no units. Consequently, there are no annoying issues in the formula for arc length when the central angle is measured in radians. Hooray!

The circumference of a circle with radius $\,r\,$ is $\,2\pi r\,.$ Circumference takes the unit of $\,r\,,$ since the real number $\,2\pi\,$ has no units.

Let $\,\theta\,$ be the radian measure of a central angle.

The arc length corresponding to $\,\theta\,$ is computed as follows:

$$ \begin{align} \cssId{s107}{s}\ &\cssId{s108}{= \left(\frac{\ \ \small\displaylines{\text{central angle}\\ \text{corresponding to}\\ \text{ desired arc length}}\ \ }{\small\displaylines{\text{central angle}\\ \text{corresponding to}\\ \text{circumference}}}\right)(\text{circumference})}\cr\cr &\cssId{s109}{= \frac{\theta}{2\pi}(2\pi r)}\cr\cr &\cssId{s110}{= \theta r \qquad \text{(cancel $\,2\pi\,$)}} \end{align} $$

Thus, the formula for arc length (written in the most conventional way) is:

$$ \cssId{s112}{s = r\theta} $$

Equivalently, we can use a proportion:

$$ \begin{gather} \cssId{s114}{\frac{\text{part angle}}{\text{whole angle}} = \frac{\text{part arc length}}{\text{whole arc length}}}\cr\cr \cssId{s115}{\frac{\theta}{2\pi} = \frac{s}{2\pi r}}\cr\cr \end{gather} $$

Cross-multiply and solve for $\,s\,$:

$$ \begin{gather} \cssId{s117}{2\pi r\theta = 2\pi s}\cr\cr \cssId{s118}{s = r\theta} \end{gather} $$

Summary: Arc Length Formula when Central Angle is Measured in Radians

$$ \cssId{s120}{\Large s = r\theta} $$

Such a beautiful and simple formula!

As an alternative to the degree-measure derivation given above, we can ‘convert’ the formula $\,s = r\theta\,$ to one that works for central angles measured in degrees, as follows.

First, convert $\,\theta^{\,\circ}\,$ to radian measure. Since $\pi\,$ radians equals $\,180^\circ\,,$ we have:

$$ \,\cssId{s125}{1 = \frac{\pi}{180^\circ}}$$

Therefore:

$$ \begin{align} \theta^{\,\circ} \ &=\ \theta^{\,\circ}\cdot 1\cr\cr &=\ \theta^\circ\cdot\frac{\pi}{180^\circ}\cr\cr &=\ \frac{\pi\theta}{180} \end{align} $$

Thus, $\,\displaystyle\frac{\pi\theta}{180}\,$ is the radian measure of $\,\theta^{\,\circ}\,.$

Substitution of this radian measure into the formula $\,s = r\theta\,$ gives

$$ \cssId{s130}{s \ =\ r\left(\frac{\pi\theta}{180}\right) \ =\ \frac{\pi r\theta}{180}} $$

which, of course, is the same formula derived above. Thus, we see that the ‘$\frac{\pi}{180}\,$’ is just a conversion factor from degree to radian measure!

Why the Name ‘Radian Measure’?

The formula $\,s = r\theta\,$ gives a beautiful insight into why the name ‘radian’ is used for radian measure. The idea was discussed in an earlier section on radian measure, but is worth repeating here!

Rewrite $\,s = r\theta\,$ (where $\,\theta\,$ is the radian measure of an angle) as $\,\theta = \frac{s}{r}\,.$ Now, think about the interpretation of the division problem $\,\frac{s}{r}\,.$

The division problem $\,\frac{10}{2}\,$ answers the question ‘How many $2$'s are there in $\,10\,$?’ Answer: $5$

Similarly, the division problem $\displaystyle\,\frac{s}{r}\,$ answers the question:

‘How many $r$'s are there in $\,s\,$?’

Answer: the radian measure of the angle!

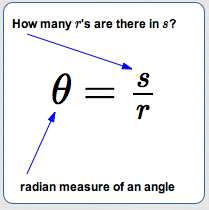
The radian measure of an angle gives the number of radiuses needed to subtend the angle!

RAD IaN
measure:

The number of
RADiuses IN
an angle

This knowledge makes it easy to visualize angles that are given in radian measure. For example, suppose you want to visualize an angle with measure $\,2.5\,$ radians.

Draw a circle of any size, as shown below. Imagine cutting a string the length of the radius of the circle. Lay this string around the circle $\,2.5\,$ times:

$$\cssId{s152}{1r + 1r + 0.5r = 2.5r}$$

Voila! You just laid off an angle with measure $\,2.5\,$ radians!

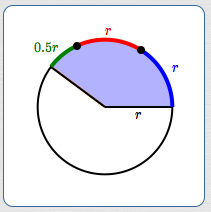
interpretation of radian measure of an angle

What does a $\,2.5\,$ radian angle look like? Lay off $\,2.5\,$ radiuses!