A Special Property of the Natural Exponential Function

Have you been following my lessons in order? If so, then you've heard me say (many times):

Exponential functions get BIG fast!

The special property of the natural exponential function discussed in this section will give you new appreciation for this fact!

The $y$-value of a Point on the Graph of the Natural Exponential Function Tells You the Slope of the Tangent Line

Usually, Calculus is needed to find slopes of tangent lines. (In particular, the derivative gives this information.)

But... for the curve $\,y = {\text{e}}^x\,$ (which is the natural exponential function) finding slopes of tangent lines is easy!

The slope of the tangent line at a point is just the $y$-value of the point!

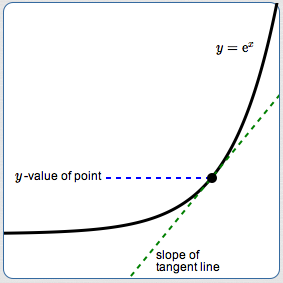
natural exponential function showing y-value of point and tangent line

For the curve $\,y = {\text{e}}^x\,$:
$y$-value of point $=$ slope of tangent line

The sketches below show just how simple things are for the natural exponential function!

If you know the $y$-value of a point, then you know the slope of the tangent line at that point.

If you know the slope of the tangent line at a point, then you know the $y$-value of the point.

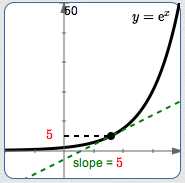
natural exponential function showing y-value of point = 5 and tangent line with slope 5

At this point, the $y$-values are changing $\,\color{red}{5}\,$ times faster than the $x$-values.

If $\,x\,$ changes by $\,0.1\,,$ we expect $\,y\,$ to change by about $\,5(0.1) = 0.5\,.$

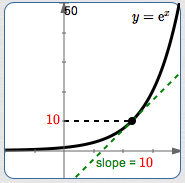
natural exponential function showing y-value of point = 10 and tangent line with slope 10

At this point, the $y$-values are changing $\,\color{red}{10}\,$ times faster than the $x$-values.

If $\,x\,$ changes by $\,0.1\,,$ we expect $\,y\,$ to change by about $\,10(0.1) = 1\,.$

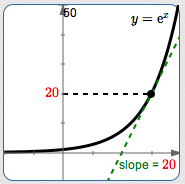
natural exponential function showing y-value of point = 20 and tangent line with slope 20

At this point, the $y$-values are changing $\,\color{red}{20}\,$ times faster than the $x$-values.

If $\,x\,$ changes by $\,0.1\,,$ we expect $\,y\,$ to change by about $\,20(0.1) = 2\,.$

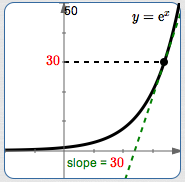
natural exponential function showing y-value of point = 30 and tangent line with slope 30

At this point, the $y$-values are changing $\,\color{red}{30}\,$ times faster than the $x$-values.

If $\,x\,$ changes by $\,0.1\,,$ we expect $\,y\,$ to change by about $\,30(0.1) = 3\,.$

Think about this.

When (say) $\,x = 10\,,$ then $\,y = {\text{e}}^{10} \approx 22{,}026\,.$ At this point, the slope of the tangent line is about $\,22{,}026\,.$ At this point, the instantaneous rate of change is about $\,22{,}026\,.$ At this point, the outputs are changing about $\,22{,}026\,$ times as fast as the inputs!

Wow! And this is only when $\,x\,$ is $\,10\,$! Exponential functions get big fast!

For Those Who Know Some Calculus and Differential Equations

The derivative of $\,f(x) = {\text{e}}^x\,$ is $\,f'(x) = {\text{e}}^x\,.$

More generally, the derivative of $\,f(x) = K{\text{e}}^x\,$ is $\,f'(x) = K{\text{e}}^x\,.$

Notice that the derivative of the function is the same as the original function. The $y$-values of points (given by the original function) and the slopes of tangent lines (given by the derivative) are the same.

We could ask: What functions are the same as their derivatives? Equivalently, we could ask: What are the solutions of the differential equation $\,y = y\,'\,$?

Head up to WolframAlpha and type in:

solve y = y'

The family of solutions is $\,y = K{\text{e}}^x\,$ (one for each real number $\,K\,$).

Scalar multiples of the natural exponential function are the ONLY functions where finding slopes of tangent lines is as easy as reading off the $y$-values of points!