 Amplitude, Period, and Phase Shift
Amplitude, Period, and Phase Shift
You need to know what the three terms amplitude, period, and phase shift mean, in the context of talking about the generalized sine and cosine curves shown below:
Generalized Sine/Cosine Curves
|
$$y = a\sin k(x + b)$$
|
$$y = a\cos k(x + b)$$
|
|
$$y = a\sin (kx + B)$$
|
$$y = a\cos (kx + B)$$
|
In these equations:
- $a\,$ and $\,k\,$ are nonzero real numbers
- $b\,$ and $\,B\,$ are any real numbers (positive, negative, or zero)
As discussed in the prior section, Graphing Generalized Sines and Cosines, each of these curves is the result of starting with either $\,y = \sin x\,$ or $\,y = \cos x\,,$ and then applying graphical transformation(s) chosen from:
These transformations affect the ‘height’ (amplitude), ‘width’ (period), and ‘left/right positioning’ (phase shift) of the resulting curve. The ideas are made precise below.
As discussed below, given any generalized sine or cosine curve, you should be able to determine its amplitude, period, and phase shift.
Sample question: State the amplitude, period, and phase shift of $\,y = 5\sin(3x-1)\,.$
In the next section, you will write an equation of a curve with a specified amplitude, period, and phase shift.
Sample question: Write an equation of a sine curve with amplitude $\,5\,,$ period $\,3\,,$ and phase shift $\,2\,.$
Summary of Key Concepts
Amplitude
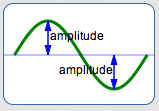
Pluck a taut string (like a guitar string) and it will vibrate, producing curves that look like sines/cosines. (If you search for ‘vibrating strings youtube’, you can see close-up and slow-motion videos of the oscillations.) The maximum displacement of the string from its ‘equilibrium’ position is called the amplitude of the oscillation.
Similarly, amplitude is the vertical distance from the $x$-axis to the highest (or lowest) point on a sine/cosine curve.
Of the graphical transformations listed above, amplitude is affected only by the vertical stretch/shrink. The vertical stretch/shrink occurs when $\,y = f(x)\,$ is changed to $\,y = a\,f(x)\,,$ by multiplying previous $y$-values by the real number $\,a\,.$ If $\,a \lt 0\,,$ then there is an additional reflection about the $x$-axis, but this does not affect the amplitude.
The amplitude of each generalized sine/cosine curve is $\,|a|\,$ (the absolute value of $\,a\,$).
Amplitude is always a positive number.
Period
Periodicity is discussed thoroughly in the prior sections Periodic Functions and The Period of a Periodic Function.
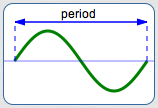
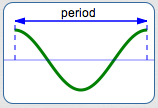
The period of each generalized sine/cosine curve is the length of one complete cycle.
Of the graphical transformations listed above, period is affected only by the horizontal stretch/shrink. The horizontal stretch/shrink occurs when $\,y = f(x)\,$ is changed to $\,y = f(kx)\,,$ by replacing every $\,x\,$ by $\,kx\,.$ Recall that transformations involving $\,x\,$ are counter-intuitive! This transformation causes a point $\,(x,y)\,$ to move to a new point $\,\bigl(\frac{x}{k},y\bigr)\,.$
Both $\,y = \sin x\,$ and $\,y = \cos x\,$ have period $\,2\pi\,.$
For $\,k \gt 0\,,$ horizontal stretch/shrink (replacing every $\,x\,$ by $\,kx\,$) changes the period to $\,\frac{2\pi}{k}\,.$
For $\,k \lt 0\,,$ the additional reflection about the $y$-axis (by replacing every $\,x\,$ by $\,-x\,$) does not cause any additional change to the period.
Therefore, the period of each generalized sine/cosine curve is $\,\frac{2\pi}{|k|}\,.$
Period is always a positive number.
Phase Shift
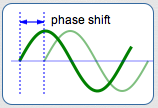
Phase shift is the trickiest one. Roughly, phase shift is the amount that the curve is shifted right or left.
Different disciplines (e.g., electrical engineering and physics) may define phase shift in slightly different ways.
Depending on the order that transformations are applied, phase shift can be affected by both shifting right/left and horizontal stretch/shrink.
Phase shift is positive (for a shift to the right) or negative (for a shift to the left).
The easiest way to find phase shift is to determine the new ‘starting point’ for the curve. That is, we'll answer the question: When is the input (argument) equal to zero?
For the argument type $\,k(x+b)\,$:
- $\,k(x+b) = 0\,$ when $\,x = -b\,$; the phase shift is $\,-b$
-
Note:
If $\,b \gt 0\,,$ the phase shift is negative.
If $\,b \lt 0\,,$ the phase shift is positive.
- For this argument type, the horizontal stretch/shrink is applied first; this doesn't move the original curve's starting point. Then, the curve is shifted right/left. In this case, the formula for phase shift involves only $\,b\,.$
For the argument type $\,kx+B\,$:
- $kx+B = 0\,$ when $\,x = \frac{-B}{k}\,$; the phase shift is $\displaystyle\,\frac{-B}{k}$
- For this argument type, the right/left shift is applied first; this moves the original curve's starting point. Then, the horizontal stretch/shrink is applied, which moves the point again. In this case, the formula for phase shift involves both $\,B\,$ and $\,k\,.$
The two phase shift formulas are consistent. For example, rewriting $\,k(x+b)\,$ in the form $\,kx+B\,$ gives:
The phase shift for the (rewritten) argument $\,k(x+b)\,$ is thus $\,\frac{-B}{k} = \frac{-kb}{k} = -b\,.$
When are these Phase Shift Formulas Meaningful?
Phase shift is most useful and meaningful for equations where:
- $k\,$ is positive (i.e., there is no reflection about the $y$-axis)
-
The size of the phase shift is less than the period (i.e., you're not shifting more than one period to the right or left).
- For arguments $\,k(x+b)\,,$ this requires that $\,|-b| \lt \frac{2\pi}{|k|}\,$; i.e., $\,|bk| \lt 2\pi$
- For arguments $\,kx+B\,,$ this requires that $\,\left|\frac{-B}{k}\right| \lt \frac{2\pi}{|k|}\,$; i.e., $\,|B| \lt 2\pi$
Although the formulas for phase shift given above can certainly be used when these conditions are not met, the resulting graphical significance is tenuous.
Given a Generalized Sine/Cosine Curve: Find Amplitude, Period, and Phase Shift
Example
State the amplitude, period, and phase shift of $\,y = 5\sin(3x-1)\,.$
Solution
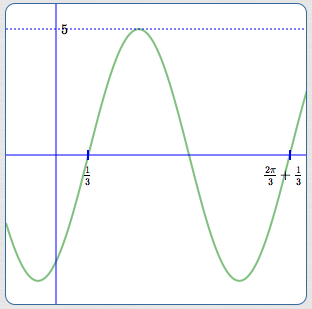
The argument is of the form $\,kx + B\,.$ The expression is of the form $\,a\sin(kx+B)\,.$ Here, $\,a = 5\,,$ $\,k = 3\,$ and $\,B = -1\,.$
The amplitude is $\,|a| = |5| = 5\,.$
The period is $\,\displaystyle\frac{2\pi}{|k|} = \frac{2\pi}{3}\,.$
Setting $\,3x-1 = 0\,$ gives $\,x = \frac{1}{3}\,$; the phase shift is $\,\frac{1}{3}\,.$
Alternatively, the phase shift is: $$\frac{-B}{k} = \frac{-(-1)}3 = \frac{1}{3}$$
Example
State the amplitude, period, and phase shift of $\,y = -3\cos 2(x+\frac{\pi}{5})\,.$
Solution
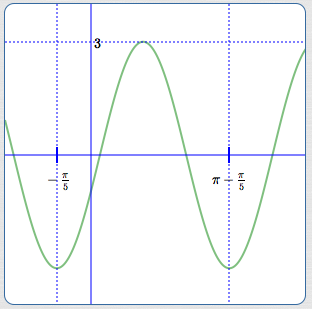
The argument is of the form $\,k(x + b)\,.$ The expression is of the form $\,a\cos k(x + b)\,.$ Here, $\,a = -3\,,$ $\,k = 2\,$ and $\,b = \frac{\pi}{5}\,.$
The amplitude is $\,|a| = |-3| = 3\,.$
The period is $\,\displaystyle\frac{2\pi}{|k|} = \frac{2\pi}{2} = \pi\,.$
Setting $\,2(x+\frac{\pi}{5}) = 0\,$ gives $\,x = -\frac{\pi}{5}\,$; the phase shift is $\,-\frac{\pi}{5}\,.$
Alternatively, the phase shift is: $$-b = -\frac{\pi}{5}$$