 Undoing a One-to-One Function; Inverse Functions
Undoing a One-to-One Function; Inverse Functions
Before reading this lesson, make sure you fully understand the concepts in the previous two lessons:
Often, you need to ‘undo’ what a function did.
For example:
- ‘Add $\,2\,$’ is undone by ‘subtract $\,2\,$’ in the following sense: if you start with any number, add $\,2\,,$ then subtract $\,2\,,$ you return to the original number
- ‘Cube’ is undone by ‘take the cube root’
- ‘Multiply by $\,3\,$’ is undone by ‘divide by $\,3\,$’
Not all functions can be ‘undone’. To ‘undo’ means to go from an output back to the input it came from—this only works if the output came from only one place!
That is, in order to ‘undo’ a function, it must satisfy the following equivalent conditions:
- Every output must have exactly one corresponding input
- The graph of the function must pass the horizontal line test
- The function must be one-to-one
When it exists, the ‘undoing’ function is given a special name—it is called the inverse function. This lesson makes these ideas precise.
Undoing a One-to-One Function
If $\,f\,$ is one-to-one, then there exists a unique function $\,f^{-1}\,$ (read as ‘$\,f\,$ inverse’) that ‘undoes’ what $\,f\,$ does, as the diagram below illustrates:
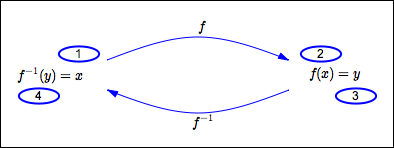
- Start with $\,x\,.$
- Let $\,f\,$ act on $\,x\,,$ giving $\,f(x)\,.$
- Rename $\,f(x)\,$ as $\,y\,.$
- Let $\,f^{-1}\,$ act on $\,y\,,$ giving $\,f^{-1}(y)\,.$
Since this returns us to where we started, $\,f^{-1}(y) = x\,.$
There are two mathematical sentences that emerge in this diagram:
| $f(x) = y$ | $f^{-1}(y) = x$ |
| ‘$\,f\,$ takes $\,x\,$ to $\,y\,$’ | ‘$\,f^{-1}\,$ takes $\,y\,$ to $\,x\,$’ |
These two sentences are equivalent—they are true at the same time, and false at the same time. This defines the relationship between a function and its inverse: if one function does something, the other undoes it!
More precisely, the equivalence of these two sentences gives all the following information:
- if $\,f\,$ takes $\,x\,$ to $\,y\,,$ then $\,f^{-1}\,$ takes $\,y\,$ back to $\,x$
- if $\,f\,$ doesn't take $\,x\,$ to $\,y\,,$ then $\,f^{-1}\,$ doesn't take $\,y\,$ to $\,x$
- if $\,f^{-1}\,$ takes $\,y\,$ to $\,x\,,$ then $\,f\,$ takes $\,x\,$ back to $\,y$
- if $\,f^{-1}\,$ doesn't take $\,y\,$ to $\,x\,,$ then $\,f\,$ doesn't take $\,x\,$ to $\,y$
Getting the Sentences $\,y = f(x)\,$ and $\,f{\,}^{-1}(y) = x\,$ From Each Other
|
Going from $\,y = f(x)\,$ to
$\,f{\,}^{-1}(y) = x\,$ :
Let $\,f^{-1}\,$ act on both sides |
|
| Start with the equation: | $y = f(x)$ |
| Let $\,f^{-1}\,$ act on both sides: | $f^{-1}(y) = f^{-1}\bigl(f(x)\bigr)$ |
| Since $\,f\,$ and $\,f^{-1}\,$ ‘undo’ each other, they ‘cancel out’ (this is made precise in the next lesson) | $f^{-1}(y) = \underbrace{f^{-1}\bigl(f(x)\bigr)}_{= x}$ |
| This leaves us with: | $f^{-1}(y) = x$ |
|
Going from $\,f{\,}^{-1}(y) = x\,$
to $\,y = f(x)\,$ :
Let $\,f\,$ act on both sides |
|||
| Start with the equation: | $f^{-1}(y) = x$ | ||
| Let $\,f\,$ act on both sides: | $f\bigl(f^{-1}(y)\bigr) = f(x)$ | ||
| Since $\,f\,$ and $\,f^{-1}\,$ ‘undo’ each other, they ‘cancel out’ (this is made precise in the next lesson) | $\underbrace{f\bigl(f^{-1}(y)\bigr)}_{= y} = f(x)$ | ||
| This leaves us with: | $y = f(x)$ | ||
Caution! $\,f{\,}^{-1}\,$ does not mean $\,\frac{1}{f}\,$!
There is some unfortunate notation used for inverse functions, which can lend itself to confusion if you're not careful.
You know from properties of exponents that $\,x^{-1}\,$ denotes the multiplicative inverse of $\,x\,.$ That is, $\,x^{-1} = \frac{1}{x}\,.$
However, when $\,f\,$ is a (one-to-one) function, then $\,f^{-1}\,$ does not mean $\,\frac{1}{f}\,$! Instead, $\,f^{-1}\,$ is just notation for the inverse of $\,f\,$—the unique function that ‘undoes’ what $\,f\,$ does. Be careful about this!
Example
Let $\,f(x) = x^3\,.$ Answer the following questions:
-
Is $\,f\,$ one-to-one? Give a reason to support your answer.
Solution: Yes. The graph of the cubing function passes the horizontal line test.
-
Does $\,f\,$ have an inverse? Give a reason to support your answer.
Solution: Yes. Every one-to-one function has an inverse.
-
Give a formula for $\,f^{-1}(x)\,.$
Solution: The cube root function undoes the cubing function: $\,f^{-1}(x) = \root 3\of{x}$
-
Specialize the equivalent sentences $\,y = f(x)\,$ and $\,f^{-1}(y) = x\,$ to the given functions.
Solution:
- $y = f(x)\,$ becomes $\,y = x^3$
- $f^{-1}(y) = x\,$ becomes $\root 3\of{y} = x$
Thus, $\,y = x^3\,$ is equivalent to $\,\root 3\of{y} = x\,.$