 The Unit Circle Approach to Trigonometry
The Unit Circle Approach to Trigonometry
There are two basic approaches to trigonometry:
- the right triangle approach (prior section)
- the unit circle approach (this section)
Both approaches were introduced in Introduction to Trigonometry. Be sure to read this prior section, since it covers important notation and conventions.
The Unit Circle Approach to Trigonometry
Start with a circle, centered at the origin, of radius $\,1\,.$ In trigonometry, this is called the ‘unit circle’. (‘Unit’ refers to the radius being equal to $\,1\,.$ ) The equation of this circle is $\,x^2 + y^2 = 1\,.$
In the unit circle approach to trigonometry, angles can have any real number measure. The angle must be ‘laid out’ in the circle in a standard way:
- Always start at the positive $x$-axis.
- Positive angles are swept out in a counterclockwise direction (start by going up).
- Negative angles are swept out in a clockwise direction (start by going down).
Let $\,\theta\,$ indicate the desired angle.
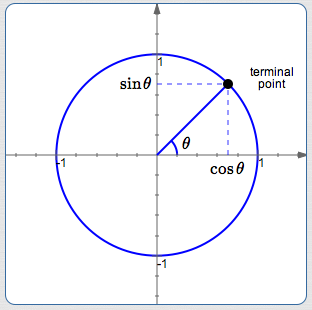
Focus attention on the point where the terminal (ending) side of the angle intersects the unit circle. This point is called the terminal point for the angle.
Once you have the terminal point, you can forget how you got there! The only thing that matters, for determining the values of the trigonometric functions, is the location of the terminal point!
The terminal point has coordinates: an $x$-value, and a $y$-value. Notice immediately that both coordinates are always numbers between $\,-1\,$ and $\,1\,$ (inclusive), since it's a point on the unit circle.
By definition:
$\sin\theta := \text{the $y$-value of the terminal point}$
$\cos\theta := \text{the $x$-value of the terminal point}$
Thus, cosine and sine are just the $\,x\,$ and $\,y\,$ values (respectively) of points on the unit circle!
Infinitely many angles can get you to the same terminal point. You might get there as efficiently as possible. You might sweep around counterclockwise many times. You might sweep around clockwise many times. It doesn't matter! All that matters is where you end up (the terminal point). This is a really important thing to remember!
The sketch below shows two ways to get to the same terminal point:
$30^\circ\,$
(Positive angles are swept out counterclockwise; up)
$-330^\circ\,$
(Negative angles are swept out clockwise; down)
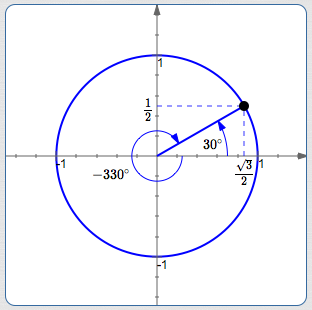
It doesn't matter how we get there! All that matters are the coordinates of the terminal point:
$\displaystyle\cos 30^\circ = \cos(-330^\circ) = \frac{\sqrt 3}{2}$
$\displaystyle \sin 30^\circ = \sin(-330^\circ) = \frac{1}{2}$
Example: Find Terminal Point, Sine, Cosine, Tangent for ‘Easy’ Angles
What is the terminal point for $\,90^\circ\,$? From this information, find (where possible) the sine, cosine, and tangent of $\,90^\circ\,.$
Solution:
As shown below, the terminal point for $\,90^\circ\,$ is $\,(0,1)\,.$
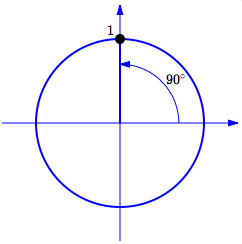
Sine is the $y$-value of the terminal point:
$$\cssId{s48}{\sin 90^\circ = 1}$$Cosine is the $x$-value of the terminal point:
$$\cssId{s50}{\cos 90^\circ = 0}$$Tangent is defined as sine divided by cosine, when the cosine is nonzero. Since division by zero is not allowed, $\,\tan 90^\circ\,$ is not defined.
Example: Given a Uniquely Identified Terminal Point, Find Trig Functions
Let $\,P(x,y)\,$ be a point on the unit circle. Let $\,\theta\,$ be any angle that has $\,P\,$ as its terminal point.
- Given that $\,y = -\frac 13\,$ and $\,x \lt 0\,,$ find $\,x\,.$
- Find (where possible) $\,\sin\theta\,,$ $\,\cos\theta\,$ and $\,\tan\theta\,.$
Solution:
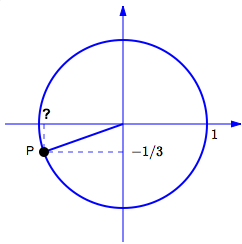
Since $\,P(x,y)\,$ is on the unit circle $\,x^2 + y^2 = 1\,,$ we have:
$$\begin{gather} \cssId{s60}{x^2 + (-\frac 13)^2 = 1}\cr\cr \cssId{s61}{x^2 + \frac 19 = 1}\cr\cr \cssId{s62}{x^2 = 1 - \frac 19 = \frac 89} \end{gather} $$Sine is the $y$-value of the terminal point:
$$ \cssId{s66}{\sin \theta = -\frac 13} $$Cosine is the $x$-value of the terminal point:
$$ \cssId{s68}{\cos \theta = -\frac{2\sqrt{2}}{3}} $$Tangent is sine divided by cosine: