Properties of Inverse Functions

This lesson will be more accessible if you fully understand the concepts in these prior lessons:
using a function box ‘backwards’
one-to-one functions
undoing a one-to-one function; inverse functions

Every one-to-one function $\,f\,$ has an inverse;
this inverse is denoted by $\,f^{-1}\,$ and read aloud as ‘$\,f\,$ inverse’.

A function and its inverse ‘undo’ each other: one function does something, the other undoes it.
The purpose of this lesson is to make this idea precise.

Review: Domain and Range of a Function

The set of allowable inputs for a function $\,f\,$ is called its domain, and is denoted by $\,\text{dom}(f)\,$.

The set of all possible outputs from a function $\,f\,$ is called its range, and is denoted by $\,\text{ran}(f)\,$.
That is, let $\,f\,$ act on every possible input—every element of its domain.
The set of resulting outputs is the range of $\,f\,$: $$\cssId{s19}{\text{ran}(f)} \cssId{s20}{= \{ f(x)\ |\ x\in\text{dom}(f) \}} $$

The Functions $\,f\,$ and $\,f^{-1}\,$ ‘Undo’ Each Other

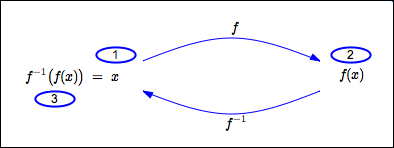
start with an allowable input for $\,f\,$;
that is, let $\,x\in\text{dom}(f)\,$
let $\,f\,$ act on $\,x\,$, giving $\,f(x)\,$
let $\,f^{-1}\,$ act on $\,f(x)\,$, giving $\,f^{-1}(f(x))\,$

This returns us to where we started, so:

$\,f^{-1}(f(x)) = x\,$ for all $\,x\,$ in the domain of $\,f\,$
In other words, the composite function $\,f^{-1}\circ f\,$
is the identity function on $\,\text{dom}(f)\,$.

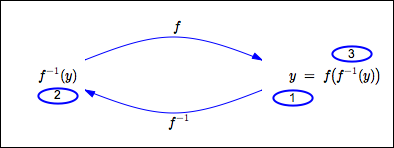
start with an output from $\,f\,$;
that is, let $\,y\in\text{ran}(f)\,$
let $\,f^{-1}\,$ act on $\,y\,$, giving $\,f^{-1}(y)\,$
let $\,f\,$ act on $\,f^{-1}(y)\,$, giving $\,f\bigl(f^{-1}(y)\bigr)\,$

This returns us to where we started, so:

$\,f\bigl(f^{-1}(y)\bigr) = y\,$ for all $\,y\,$ in the range of $\,f\,$
In other words, the composite function $\,f\circ f^{-1}\,$
is the identity function on $\,\text{ran}(f)\,$.

Input/Output Roles Reversed for $\,f\,$ and $\,f^{-1}\,$

The input/output roles for a function and its inverse are reversed—the inputs to one are the outputs from the other.
This fact has some nice consequences:

POINTS ON THE GRAPHS OF $\,f\,$ and $\,f^{-1}\,$ HAVE THEIR COORDINATES SWITCHED:

$\,(a,b)\,$ is on the graph of $\,f\,$ if and only if $\,(b,a)\,$ is on the graph of $\,f^{-1}\,$

DOMAIN AND RANGE OF $\,f^{-1}\,$:

the inputs to $\,f^{-1}\,$ are the outputs from $\,f\,$: that is, $\,\text{dom}(f^{-1}) = \text{ran}(f)$
the outputs from $\,f^{-1}\,$ are the inputs to $\,f\,$: that is, $\,\text{ran}(f^{-1}) = \text{dom}(f)$

SUMMARY: PROPERTIES OF INVERSE FUNCTIONS

For your convenience, the properties of inverse functions discussed in this and earlier exercises are summarized below.

PROPERTIES OF INVERSE FUNCTIONS

A function $\,g\,$ has an inverse if and only if $\,g\,$ is a one-to-one function.

Let $\,f\,$ be a one-to-one function.
The inverse of $\,f\,$ is denoted by $\,f^{-1}\,$ and read aloud as ‘$\,f\,$ inverse’.

The functions $\,f\,$ and $\,f^{-1}\,$ satisfy the following properties:

$\,f^{-1}\,$ is also a one-to-one function
the inverse of $\,f^{-1}\,$ is $\,f\,$
$\,f(x) = y\,$ if and only if $\,f^{-1}(y) = x\,$
$\,f^{-1}(f(x)) = x\,$ for all $\,x\in\text{dom}(f)\,$
$\,f\bigl(f^{-1}(y)\bigr) = y\,$ for all $\,y\in\text{ran}(f)\,$
$(a,b)$ is on the graph of $\,f\,$ if and only if $\,(b,a)\,$ is on the graph of $\,f^{-1}\,$
$\text{dom}(f^{-1}) = \text{ran}(f)\,$ and $\text{ran}(f^{-1}) = \text{dom}(f)\,$

Master the ideas from this section
by practicing the exercise at the bottom of this page.

When you're done practicing, move on to:
finding inverse functions
(when there's only one $\,x\,$ in the formula)