Linear Versus Exponential Functions

Linear functions ($\,y = mx + b\,$) and exponential functions ($\,y = b^x\,$) are both extremely important. However, they behave very differently, and it's important that you thoroughly understand this difference.

In particular, you should be able to recognize linear and exponential behavior when looking at tables of input/output pairs which have equally-spaced inputs; this is covered in the next section.

Here's what you need to think about for this lesson:

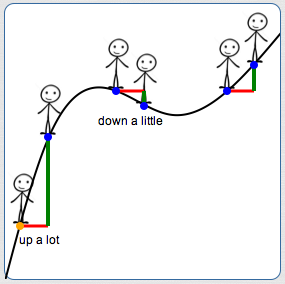
Imagine that you're walking along the graph of a function, moving from left to right. You stop at a point.

Then, you move a fixed amount in the horizontal direction. How does your ‘elevation’ change? That is, how do you change vertically?

Keep walking. Stop at a different point. Move the same horizontal amount. Now, how much do you change vertically?

Repeat.

For general functions, you can't say much about your vertical movements. Sometimes you move up. Sometimes you move down. Sometimes a little. Sometimes a lot. No consistent information.

For linear and exponential functions, however, your up/down movement is completely predictable!

Make the Notation Mathematical

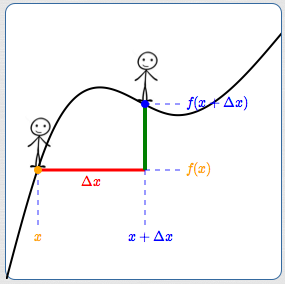
Firstly, let's firm up the notation. A person walking along a graph doesn't lend itself particularly well to mathematical formulation!

For the graph of a given function $\,f\,$:

Call the point you're initially standing on $\,\color{orange}{(x,f(x))}\,.$
Call the amount you move horizontally $\,\color{red}{\Delta x}\,$ (read as ‘delta $x$’). This symbol $\,\Delta x\,$ represents the ‘change in $\,x\,$’. If you move to the right, then $\,\Delta x\,$ is positive. If you move to the left, then $\,\Delta x\,$ is negative.
The $x$-value of the new point is $\,\color{blue}{x + \Delta x}\,.$ If $\,\Delta x \gt 0\,,$ then $\,x + \Delta x\,$ lies to the right of $\,x\,.$ If $\,\Delta x \lt 0\,,$ then $\,x + \Delta x\,$ lies to the left of $\,x\,.$
The $y$-value of the new point is $\,\color{blue}{f(x + \Delta x)}\,.$

GOAL:

Predict the new $y$-value, $\,\color{blue}{f(x+\Delta x)}\,,$ in terms of the original $y$-value, $\,\color{orange}{f(x)}\,.$ That is, get a formula that looks like:

$$ \begin{align} &f(x+\Delta x)\cr &\quad = \text{something involving $\,f(x)\,$} \end{align} $$

How Does $\,f(x+\Delta x)\,$ Relate To $\,f(x)\,$ For Linear Functions?

In the earlier section Working with Linear Functions, we learned that for a linear function $\,f(x) = mx + b\,$:

$$ \begin{align} &\cssId{s44}{\overbrace{f(x+\Delta x)}^{\text{new $y$-value}}}\cr\cr &\quad \cssId{s45}{\ \ = \overbrace{\color{red}{f(x) + m\Delta x}}^{\text{formula involving original $\,y\,$-value}}} \end{align} $$

What Is That Formula On The Right Telling Us About The New $y$-Value?

For linear functions, what is the new $y$-value, $\,f(x+\Delta x)\,$? Answer: It is $\,f(x) + m\Delta x\,.$ So, the new $y$-value is the same as the original $y$-value, except that $\,m\Delta x\,$ is added to it.

Notice that the formula for $\,f(x+\Delta x)\,$ (the ‘new elevation’) depends on three things:

The original $y$-value, $\,f(x)\,$ (the elevation you came from).
The change in $\,x\,,$ $\,\Delta x\,$ (how far you're stepping away from the original point, and in what direction).
The slope of the line, $\,m\,$ (how steep the line is).

So, how does a linear function change? When the input changes by $\,\Delta x\,,$ the output changes by $\,m\Delta x\,.$ That is, the outputs are changing $\,m\,$ times faster than the inputs are changing.

You already know this result well from years of working with linear functions. However, it is important to review before contrasting with the very different behavior of exponential functions.

How Does $\,f(x+\Delta x)\,$ Relate To $\,f(x)\,$ For Exponential Functions?

Let's now consider exponential functions.

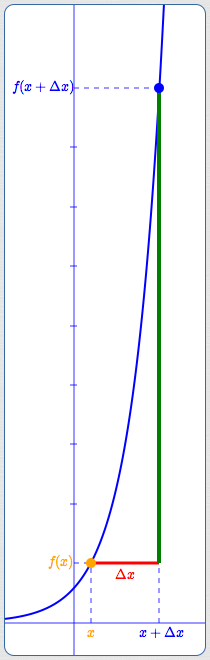
Let $\,f(x) = a^x\,$ for $\,a \gt 0\,,$ $\,a\ne 1\,.$ (The graph above shows an exponential function for $\,a \gt 1\,.$ ) The function $\,f\,$ takes an input and raises $\,a\,$ to that power. Then,

$$ \begin{align} &\cssId{s66}{f(x+\Delta x)\ }\cr &\qquad\cssId{s67}{= a^{x + \Delta x}}\cr &\qquad\quad\cssId{s68}{\text{(definition of $\,f\,$)}}\cr\cr &\qquad\cssId{s69}{= a^xa^{\Delta x}}\cr &\qquad\quad\cssId{s70}{\text{(exponent law)}}\cr\cr &\qquad\cssId{s71}{= a^{\Delta x}\cdot f(x)}\cr &\qquad\quad\cssId{s72}{\text{(since $\,f(x) = a^x\,$)}} \end{align} $$

Thus, for exponential functions:

$$ \cssId{s74}{f(x+\Delta x) = \color{red}{a^{\Delta x}\cdot f(x)}} $$

What Is That Formula On The Right Telling Us About The New $y$-Value?

For exponential functions, what is the new $y$-value, $\,f(x+\Delta x)\,$? Answer: It is $\,a^{\Delta x}\cdot f(x)\,.$

So, the new $y$-value is the same as the original $y$-value, except that it is multiplied (scaled) by $\,a^{\Delta x}\,.$

Notice that the formula for $\,f(x+\Delta x)\,$ (the ‘new elevation’) depends on three things:

The original $y$-value, $\,f(x)\,$ (the elevation you came from).
The change in $\,x\,,$ $\,\Delta x\,$ (how far you're stepping away from the original point, and in what direction).
The base of the exponential function, $\,a\,$ (which determines how steep the curve is).

So, how does an exponential function change? When the input changes by $\,\Delta x\,,$ the current output gets multiplied by $\,a^{\Delta x}\,.$ The multiplier $\,a^{\Delta x}\,$ is sometimes called the scaling factor. The original $y$-value is scaled by $\,a^{\Delta x}\,.$

In the (tall!) sketch above:

The exponential function is $\,f(x) = 3^x\,,$ so $\,a = 3\,.$
The width of the red segment (which represents $\,\Delta x\,$) is $\,2\,.$
The scaling factor is therefore $\,a^{\Delta x} = 3^2 = 9\,.$
The new $y$-value is $\,9\,$ times bigger than the original $y$-value! (Look carefully at the tick marks along the vertical axis.)
Exponential functions get big fast!