Absolute Value as Distance Between Two Numbers

To find the distance between any two real numbers, take the greater number (the one lying farthest to the right on a number line) and subtract the lesser number (the one lying farthest to the left).

That is, if $\,x \ge y\,,$ then the distance between them is just the difference, $\,x - y\,.$ For example, the distance between $\,-3\,$ and $\,5\,$ is: $\,5 - (-3) = 8\,$

But what if you goof up the order of subtraction? In this case, you get a number with the right size (distance from zero), but the wrong sign: $\,-3 - 5 = -8\,.$ To get from $\,-8\,$ to the answer you really want, just take the absolute value!

Thus, absolute value provides a convenient way to talk about the distance between any two real numbers:

DISTANCE BETWEEN TWO REAL NUMBERS absolute value of the difference

Let $\,x\,$ and $\,y\,$ be real numbers. Then: $$ \cssId{s14}{|x-y| = \text{the distance between } \,x\, \text{ and } \,y} $$

That is, to find the distance between any two real numbers:

Subtract them in any order
Take the absolute value of the result

Notice that you don't need to know which number is greater (if the numbers are different) to find the distance between them. And, of course, if two numbers are equal, then the distance between them is zero.

Notice that $\,x - y\,$ and $\,y - x\,$ are opposites, since $\,x - y = -(y - x)\,.$ Opposites have the same distance from zero, hence have the same absolute value. (Remember: absolute value gives distance from zero!) Thus, $\,|x - y\,| = |y - x|\,.$ So we repeat—you can subtract in whatever order you want!

By recognizing an absolute value expression as representing a distance between two numbers, many simple absolute value sentences can be solved ‘by inspection’—just look at them, think, and write down the solution set!

Here are some examples:

Examples

Example: Solving a ‘Less Than’ Absolute Value Sentence By Inspection

Solve: $|x - 1| \lt 2$

Solution: View $\,|x - 1|\,$ as the distance between $\,x\,$ and $\,1\,.$ Here, we want all numbers $\,x\,$ whose distance from $\,1\,$ is less than $\,2\,$:

$$ \cssId{s35}{\overbrace{\strut |x-1|}^{\text{want numbers $x$ whose distance from $1\ \ldots \ $ }}} \cssId{s36}{\overbrace{\strut \ \ \lt 2\ \ }^{\text{is less than two}}} $$

Mark the number $\,1\,$ on a number line; we want all numbers that are less than $\,2\,$ units away.
Starting at $\,1\,,$ go $\,2\,$ units to the right; mark $\,1 + 2 = 3\,$ on the number line.
Starting at $\,1\,,$ go $\,2\,$ units to the left; mark $\,1 - 2 = -1\,$ on the number line.
Since we want the distance from $\,1\,$ to be strictly less than $\,2\,,$ put hollow dots at the endpoints.
Shade everything between $\,-1\,$ and $\,3\,.$

Interval notation for solution set: $\,(-1,3)$

Sentence form of solution: $\,-1 \lt x \lt 3\,$

Example: Solving a ‘Greater Than’ Absolute Value Sentence By Inspection

Solve: $|x + 3| \ge 1$

Solution: First, rewrite $\,|x+3|\,$ so there is a difference inside the absolute value: $$\cssId{s54}{|x + 3\,| = |x - (-3)|}$$ Thus, $\,|x+3|\,$ represents the distance between $\,x\,$ and $\,-3\,.$

Here, we want all numbers $\,x\,$ whose distance from $\,-3\,$ is greater than or equal to $\,1\,$:

$$ \begin{gather} \cssId{s57}{|x+3| \ge 1}\cr\cr \cssId{s58}{|x - (-3)| \ge 1}\cr\cr \cssId{s59}{\overbrace{\strut |x-(-3)|}^{\text{want numbers $x$ whose distance from $-3\ \ldots \ $ }}} \cssId{s60}{\overbrace{\strut \ \ \ge 1\ \ }^{\text{is greater than or equal to $\,1$}}} \end{gather} $$

Mark the number $\,-3\,$ on a number line; we want all numbers that are $\,1\,$ or more units away.
Starting at $\,-3\,,$ go $\,1\,$ unit to the right; mark $\,-3 + 1 = -2\,$ on the number line.
Starting at $\,-3\,,$ go $\,1\,$ unit to the left; mark $\,-3 - 1 = -4\,$ on the number line.
Since we want the distance from $\,-3\,$ to be greater than or equal to $\,1\,,$ put solid dots at the endpoints.
Shade everything to the right of $\,-2\,$ and to the left of $\,-4\,.$

Interval notation for solution set: $\,(-\infty,-4] \cup [-2,\infty)$

Sentence form of solution: $\,x \le -4 \ \ \text{ or }\ \ x \ge -2\,$

Example: Solving a Compound Absolute Value Sentence By Inspection

This final example is important in Calculus. When you study the precise definition of a limit (which is the central concept in Calculus), then you'll see this type of absolute value sentence.

Solve: $\,0 \lt |x - 2| \lt \delta\,$

Solution: The symbol ‘$\,\delta\,$’ is the lowercase Greek letter delta. It is used in this context to denote a small positive number.

The sentence ‘$\,0 \lt |x - 2| \lt \delta\,$’ is a compound inequality—it uses more than one inequality symbol. This type of compound inequality is a shorthand for a mathematical ‘and’ sentence:

$$ \begin{gather} \cssId{s86}{0 \lt |x - 2| \lt \delta}\cr \cssId{s87}{\text{ is equivalent to }}\cr \cssId{s88}{0 \lt |x - 2|\ \text{ and }\ |x - 2| \lt \delta} \end{gather} $$

Recall that the only time an ‘and’ sentence is true is when both subsentences are true. So, here's what you should think:

$$ \begin{gather} \cssId{s91}{\overbrace{\strut |x - 2|}^{\text{want numbers $x$ whose distance from $2\ \ldots$ } }} \cssId{s92}{\overbrace{\strut \ \ \gt 0\ \ }^{\text{is greater than $0$} }}\cr\cr \cssId{s93}{\overbrace{\strut \text{ and }}^{\text{ and }}}\cr\cr \cssId{s94}{\overbrace{\strut |x - 2|}^{\text{ whose distance from $2\ \ldots$ } }} \cssId{s95}{\overbrace{\strut \lt \delta}^{\text{is less than delta}}} \end{gather} $$

That is, the solutions to ‘$\,0 \lt |x - 2| \lt \delta\,$’ are all numbers that are within $\,\delta\,$ units of $\,2\,,$ but not equal to $\,2\,.$

More precisely, study the number lines below:

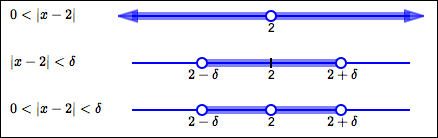
The top number line (labeled ‘$\,0 \lt |x - 2|\,$’) has everything shaded except $\,2\,.$ These are the numbers whose distance from $\,2\,$ is strictly greater than zero.
The middle number line (labeled ‘$\,|x - 2| \lt \delta\,$’) shades all numbers that are less than $\,\delta\,$ units from $\,2\,$:
- Starting at $\,2\,,$ go $\,\delta\,$ to the right; mark $\,2+\delta\,$ on the number line.
- Starting at $\,2\,,$ go $\,\delta\,$ to the left; mark $\,2 - \delta\,$ on the number line.
- Shade everything between $\,2-\delta\,$ and $\,2+\delta\,.$
The bottom number line (labeled ‘$\,0 \lt |x-2| \lt \delta\,$’) shows the intersection (the overlap) of the shaded sets on the top and middle, which is the desired solution set.

The resulting solution set is often called a ‘punctured neighborhood of $\,2\,$’:

It is a neighborhood of $\,2\,$ (an open set that contains $\,2\,$) ...
... except that the $\,2\,$ is missing—it is punctured at $\,2\,.$

Now that you've seen all the details, you should never have to do this much work again! You should merely think:

The ‘$\,|x-2| \lt \delta\,$’ part gives all the numbers between $\,2-\delta\,$ and $\,2+\delta\,.$ (Mark the $\,2\,,$ go $\,\delta\,$ to the left and $\,\delta\,$ to the right, shade everything in between.)
The ‘$\,0 \lt |x-2|\,$’ part takes away the $\,2\,.$ (Put a hollow dot at $\,2\,.$)

Easy!

Interval notation for solution set: $$(2-\delta,2) \cup (2,2+\delta)$$

Sentence form of solution: $$2-\delta \lt x \lt 2 \ \ \text{ or }\ \ 2 \lt x \lt 2+\delta$$

Equivalent sentence form of solution: $$2-\delta \lt x \lt 2+\delta \ \ \text{ and }\ \ x\ne 2$$

Solving Absolute Value Sentences at WolframAlpha

For fun, zip up to WolframAlpha and type in any of these:

|x - 1| < 2
(Look carefully—the vertical bar used for absolute value should be somewhere on your keyboard.)
|x + 3| ≥ 1
0 < |x - 2| < 0.3