 Doubling Time, Half-Life
Doubling Time, Half-Life
Exponential behavior (growth/decay) is defined by: equal changes in the input cause the output to be multiplied by a constant.
Once you've recognized exponential behavior then you can always use $\,P(t) = P_0\,{\text{e}}^{rt}\,$ as your model. Here, $\,P(t)\,$ is the population at time $\,t\,,$ $\,P_{0}\,$ is the population at time zero, and $\,r\,$ is the relative growth rate.
However, if an (equal change, constant multiplier) = $\,(\Delta t,b)\,$ pair is readily available, then the model $\,P(t) = P_0\,b^{t/\Delta t}\,$ is more natural and easier to use.
A variety of problems involving exponential functions were explored in Solving Exponential Growth and Decay Problems. This current section focuses on doubling time, half-life, and related problems.
-
Doubling Time ($\,d\,$):
- Doubling time formula derived from $\,P(t) = P_0\,{\text{e}}^{rt}\,$: $$\cssId{s10}{d = \frac{\ln 2}{r}}$$
- Doubling time formula derived from $\,P(t) = P_0\,b^{t/\Delta t}\,$: $$\cssId{s12}{d = \frac{\ln 2}{\ln b}\cdot \Delta t}$$
-
What is the relative growth rate
for $\,P_0b^{t/\Delta t}\,$?
Answer: $$r = \frac{\ln b}{\Delta t}$$
- Compatibility of the two doubling time formulas
-
Half-Life ($\,h\,$):
- Half-life formula derived from $\,P(t) = P_0\,{\text{e}}^{rt}\,$: $$\cssId{s18}{h = \frac{\ln 0.5}{r} = -\frac{\ln 2}{r}}$$
- Half-life formula derived from $\,P(t) = P_0\,b^{t/\Delta t}\,$: $$\cssId{s20}{h = \frac{\ln 0.5}{\ln b}\cdot \Delta t = -\frac{\ln 2}{\ln b}\cdot \Delta t}$$
-
Generalization: How long ($\,g\,$) does it take for a population to go from $\,P(t)\,$ to $\,kP(t)\,,$ for $\,k \gt 0\,$? Answer:
- For $\,P(t) = P_0\,{\text{e}}^{rt}\,$: $$\cssId{s25}{g = \frac{\ln k}{r}}$$
- For $\,P(t) = P_0\,b^{t/\Delta t}\,$: $$\cssId{s27}{g = \frac{\ln k}{\ln b}\cdot \Delta t}$$
Doubling Time
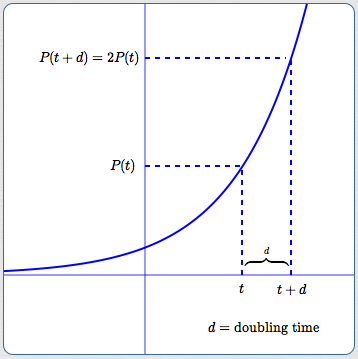
Doubling Time Formula Derived From $\,P(t) = P_0\,{\text{e}}^{rt}$
Doubling time $\,d\,$ depends only on the relative growth rate, $\,r\,.$ It does not depend on time!
Consequently, for exponential functions, the current population size doesn't matter; it always takes the same amount of time for a population to double.
Let $\,P(t) = P_{0}{\text{e}}^{rt}\,$ for $\,r \gt0\,$ (so this is exponential growth). Let $\,d\,$ denote the doubling time, so that $\,P(t+d) = 2P(t)\,$:
$\displaystyle\,\overbrace{\cancel{P_{0}}{\text{e}}^{r(t+d)}}^{P(t+d)} = \overbrace{2\cancel{P_{0}}{\text{e}}^{rt}}^{2P(t)}\,$
Solve for $\,d\,$ by dividing both sides by $\,r\,.$
Doubling Time Formula Derived From $\,P(t) = P_0\,b^{t/\Delta t}$
As above, doubling time does not depend on time! It depends only on the (equal change, constant multiplier) = $\,(\Delta t,b)\,$ pair.
Let $\,P(t) = P_{0}b^{t/\Delta t}\,$ for $\,b \gt 1\,$ (so this is exponential growth). Let $\,d\,$ denote the doubling time, so that $\,P(t+d) = 2P(t)\,$:
$$\cssId{s57}{\overbrace{\cancel{P_0}b^{(t+d)/\Delta t}}^{P(t+d)} = \overbrace{2\cancel{P_0}b^{t/\Delta t}}^{2P(t)}}$$ $$\begin{gather} \cssId{s58}{\cancel{b^{t/\Delta t}} b^{d/\Delta t} = 2\cancel{b^{t/\Delta t}}}\cr \cssId{s59}{\text{(Note that $\,t\,$ disappears at this step!)}} \end{gather} $$ $$\cssId{s60}{b^{d/\Delta t} = 2}$$ $$\cssId{s61}{\ln b^{d/\Delta t} = \ln 2}$$ $$\cssId{s62}{\frac{d}{\Delta t}\ln b = \ln 2}$$ $$\cssId{s63}{ d = \frac{\ln 2}{\ln b}\cdot \Delta t}$$What is the Relative Growth Rate for $\,P_{0}b^{t/\Delta t}\,$?
Putting $\,P(t) = P_{0}b^{t/\Delta t}\,$ in the form $\,P(t) = P_{0}{\text{e}}^{rt}\,$ yields:
$$ \begin{align} &\cssId{s68}{P_{0}\,b^{t/\Delta t}}\cr\cr &\quad \cssId{s69}{= P_{0}\,{\text{e}}^{\ln( b^{t/\Delta t})}}\cr\cr &\quad \cssId{s70}{= P_{0}\,{\text{e}}^{(t/\Delta t)\ln b}}\cr\cr &\quad \cssId{s71}{= P_{0}\,{\text{e}}^{t\,\overbrace{(\ln b)/\Delta t}^{r}}} \end{align} $$Compatibility of the Two Doubling Time Formulas
Using the fact that $\displaystyle\,r = \frac{\ln b}{\Delta t}\,,$ we have:
$$\begin{align} d \ &=\ \cssId{s75}{\frac{\ln 2}{\ln b}\cdot \Delta t}\cr &\quad \text{(the doubling time for $P_0\,b^{\frac{t}{\Delta t}})$}\cr\cr &\ \cssId{s76}{= \frac{\ln 2}{(\ln b/\Delta t)}}\cr &\quad \text{(use the fact that $\Delta t = \frac{1}{1/\Delta t}$)}\cr\cr &\ \cssId{s77}{= \frac{\ln 2}{r}}\cr &\quad \text{(the doubling time for $P_0\,{\text{e}}^{rt}$)} \end{align} $$Half-Life
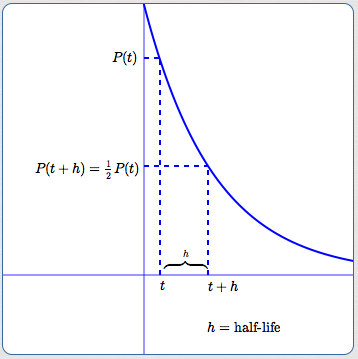
Half-life is the time it takes for a current amount to be cut in half.
Half-Life Formula Derived From $\,P(t) = P_{0}{\text{e}}^{rt}$
Again, half-life depends only on the relative growth rate, $\,r\,.$ It does not depend on time!
Let $\,P(t) = P_{0}{\text{e}}^{rt}\,$ for $\,r \lt 0\,$ (so this is exponential decay). Let $\,h\,$ denote the half-life, so $\,P(t+h) = \frac 12P(t)\,$:
$$ \begin{gather} \cssId{s85}{\overbrace{\cancel{P_{0}}{\text{e}}^{r(t+h)}}^{P(t+h)} = \overbrace{\frac 12\cancel{P_{0}}{\text{e}}^{rt}}^{\frac 12P(t)}}\cr\cr \cssId{s86}{\bcancel{{\text{e}}^{rt}}{\text{e}}^{rh} = \frac 12\bcancel{{\text{e}}^{rt}}}\cr \cssId{s87}{\text{(Note that $\,t\,$ disappears at this step!)}}\cr\cr \cssId{s88}{\ln {\text{e}}^{rh} = \ln \frac 12 = \ln 0.5}\cr\cr \cssId{s89}{rh = \ln 0.5}\cr\cr \cssId{s90}{h = \frac{\ln 0.5}{r} = \frac{\ln 2^{-1}}{r} = -\frac{\ln 2}{r}}\cr\cr \end{gather} $$Note that since $\,r \lt 0\,$ for exponential decay, we have $\displaystyle \,h = -\frac{\ln 2}{r} \gt 0\,.$
Half-Life Formula Derived From $\,P(t) = P_{0}b^{t/\Delta t}$
As above, half-life does not depend on time! It depends only on the (equal change, constant multiplier) = $\,(\Delta t,b)\,$ pair.
Let $\,P(t) = P_{0}b^{t/\Delta t}\,$ for $\,0 \lt b \lt 1\,$ (so this is exponential decay). Let $\,h\,$ denote the half-life, so that $\,P(t+h) = \frac 12P(t)\,$:
$$ \begin{gather} \cssId{s99}{\overbrace{\cancel{P_0}b^{(t+h)/\Delta t}}^{P(t+h)} = \overbrace{\frac 12\cancel{P_0}b^{t/\Delta t}}^{\frac 12P(t)}}\cr\cr \cssId{s100}{\cancel{b^{t/\Delta t}} b^{h/\Delta t} = \frac 12\cancel{b^{t/\Delta t}}}\cr \cssId{s101}{\text{(Note that $\,t\,$ disappears at this step!)}}\cr\cr \cssId{s102}{b^{h/\Delta t} = \frac 12 = 0.5}\cr\cr \cssId{s103}{\ln b^{h/\Delta t} = \ln 0.5}\cr\cr \cssId{s104}{\frac{h}{\Delta t}\ln b = \ln 0.5} \end{gather} $$Note that since $\,0 \lt b \lt 1\,$ for exponential decay, we have $\,\ln b \lt 0\,,$ and thus $\displaystyle h = -\frac{\ln 2}{\ln b}\cdot \Delta t \gt 0\,.$
Generalization: How Long Does it Take for a Population to Go From $\,P(t)\,$ to $\,kP(t)\,$?
Let $\,g\,$ be the time it takes to go from $\,P(t)\,$ to $\,kP(t)\,$ for any $\,k \gt 0\,.$ The derivation is identical to those above, hence is greatly abbreviated here: