Shifting Graphs Up/Down Left/Right

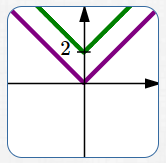
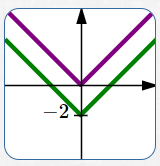
$y = f(x)$ $y = f(x) + 2$ Up $2$	$y = f(x)$ $y = f(x) - 2$ Down $2$
Movements up and down change the $y$-values of points. Transformations that affect the $y$-values are intuitive. For example, to move up $\,2\,,$ you add $\,2\,$ to the previous $y$-value.

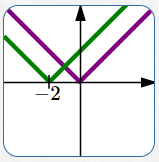
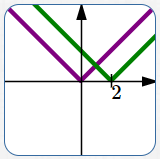
$y = f(x)$ $y = f(x+2)\,$ Left $2$	$y = f(x)$ $y = f(x-2)\,$ Right $2$
Movements left and right change the $x$-values of points. Transformations that affect the $x$-values are counter-intuitive. For example, to move left $\,2\,,$ you replace every $\,x\,$ by $\,x+2\,,$ not $\,x-2\,.$

The lesson Graphing Tools: Vertical and Horizontal Translations in the Algebra II curriculum gives a thorough discussion of shifting graphs up/down left/right. The key concepts are repeated here.

The exercises in this lesson duplicate those in Graphing Tools: Vertical and Horizontal Translations.

• Points on the graph of $\,y=f(x)\,$ are of the form $\,\bigl(x,f(x)\bigr)\,.$

  Points on the graph of $\,y=f(x)+3\,$ are of the form $\,\bigl(x,f(x)+3\bigr)\,.$

  Thus, the graph of $\,y=f(x)+3\,$ is the same as the graph of $\,y=f(x)\,,$ shifted UP three units.

• Transformations involving $\,y\,$ work the way you would expect them to work—they are intuitive.

• Here is the thought process you should use when you are given the graph of $\,y=f(x)\,$ and asked about the graph of $\,y=f(x)+3\,$:

Summary of Vertical Translations

Let $\,p\,$ be a positive number.

Start with the equation $\,\color{purple}{y=f(x)}\,.$ Adding $\,\color{green}{p}\,$ to the previous $\color{green}{y}$-values gives the new equation $\,\color{green}{y=f(x)+p}\,.$ This shifts the graph UP $\,\color{green}{p}\,$ units.

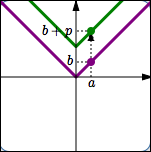
A point $\,\color{purple}{(a,b)}\,$ on the graph of $\,\color{purple}{y=f(x)}\,$ moves to a point $\,\color{green}{(a,b+p)}\,$ on the graph of $\,\color{green}{y=f(x)+p}\,.$

Additionally:

Start with the equation $\,\color{purple}{y=f(x)}\,.$ Subtracting $\,\color{green}{p}\,$ from the previous $\color{green}{y}$-values gives the new equation $\,\color{green}{y=f(x)-p}\,.$ This shifts the graph DOWN $\,\color{green}{p}\,$ units.

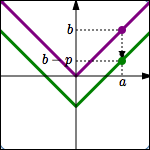
A point $\,\color{purple}{(a,b)}\,$ on the graph of $\,\color{purple}{y=f(x)}\,$ moves to a point $\,\color{green}{(a,b-p)}\,$ on the graph of $\,\color{green}{y=f(x)-p}\,.$

This transformation type (shifting up and down) is formally called vertical translation.

Ideas Regarding Horizontal Translations (Moving Left/Right)

• Points on the graph of $\,y=f(x)\,$ are of the form $\,\bigl(x,f(x)\bigr)\,.$

  Points on the graph of $\,y=f(x+3)\,$ are of the form $\,\bigl(x,f(x+3)\bigr)\,.$

• How can we locate these desired points $\,\bigl(x,f(x+3)\bigr)\,$?

  First, go to the point $\,\color{red}{P\bigl(x+3\,,\,f(x+3)\bigr)}\,$ on the graph of $\,\color{red}{y=f(x)}\,.$

  

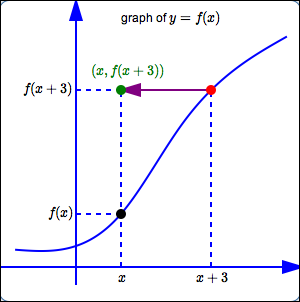
  This point has the $y$-value that we want, but it has the wrong $x$-value.

  Move this point $\,\color{purple}{3}\,$ units to the left. Thus, the $y$-value stays the same, but the $x$-value is decreased by $\,3\,.$ This gives the desired point $\,\color{green}{\bigl(x,f(x+3)\bigr)}\,.$

  Thus, the graph of $\,y=f(x+3)\,$ is the same as the graph of $\,y=f(x)\,,$ shifted LEFT three units.

  Thus, replacing $\,x\,$ by $\,x+3\,$ moved the graph LEFT (not right, as might have been expected!)

• Transformations involving $\,x\,$ do NOT work the way you would expect them to work! They are counter-intuitive—they are against your intuition.

• Here is the thought process you should use when you are given the graph of $\,y=f(x)\,$ and asked about the graph of $\,y=f(x+3)\,$:

  $$ \begin{align} \text{original equation:} &\quad y=f(x)\cr \text{new equation:} &\quad y=f(x+3) \end{align} $$
  $$ \begin{gather} \text{Interpretation of new equation:}\cr\cr y = f( \overset{\text{replace $x$ by $x+3$}}{\overbrace{ x+3}} ) \end{gather} $$

  Replacing every $\,x\,$ by $\,x+3\,$ in an equation moves the graph $\,3\,$ units TO THE LEFT.

Summary of Horizontal Translations

Let $\,p\,$ be a positive number.

Start with the equation $\,\color{purple}{y=f(x)}\,.$ Replace every $\,\color{green}{x}\,$ by $\,\color{green}{x+p}\,$ to give the new equation $\,\color{green}{y=f(x+p)}\,.$ This shifts the graph LEFT $\,\color{green}{p}\,$ units.

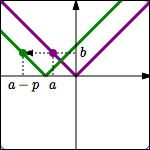
A point $\,\color{purple}{(a,b)}\,$ on the graph of $\,\color{purple}{y=f(x)}\,$ moves to a point $\,\color{green}{(a-p,b)}\,$ on the graph of $\,\color{green}{y=f(x+p)}\,.$

Additionally:

Start with the equation $\,\color{purple}{y=f(x)}\,.$ Replace every $\,\color{green}{x}\,$ by $\,\color{green}{x-p}\,$ to give the new equation $\,\color{green}{y=f(x-p)}\,.$ This shifts the graph RIGHT $\,\color{green}{p}\,$ units.

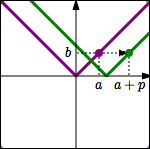
A point $\,\color{purple}{(a,b)}\,$ on the graph of $\,\color{purple}{y=f(x)}\,$ moves to a point $\,\color{green}{(a+p,b)}\,$ on the graph of $\,\color{green}{y=f(x-p)}\,.$

Different Words Used to Talk About Transformations Involving $\,y\,$ and $\,x\,$

Notice that different words are used when talking about transformations involving $\,y\,,$ and transformations involving $\,x\,.$

For transformations involving $\,y\,$ (that is, transformations that change the $y$-values of the points), we say:

DO THIS to the previous $y$-value

For transformations involving $\,x\,$ (that is, transformations that change the $x$-values of the points), we say:

REPLACE the previous $x$-values by $\ldots$

Make Sure You See the Difference!

Vertical translations:
Going from $\,y=f(x)\,$ to $\,y = f(x) \pm c\,$

Horizontal translations:
Going from $\,y = f(x)\,$ to $\,y = f(x\pm c)\,$

Make sure you see the difference between (say) $\,y = f(x) + 3\,$ and $\,y = f(x+3)\,$!

In the case of $\,y = f(x) + 3\,,$ the $\,3\,$ is ‘on the outside’: we're dropping $\,x\,$ in the $\,f\,$ box, getting the corresponding output, and then adding $\,3\,$ to it. This is a vertical translation.

In the case of $\,y = f(x + 3)\,,$ the $\,3\,$ is ‘on the inside’: we're adding $\,3\,$ to $\,x\,$ before dropping it into the $\,f\,$ box. This is a horizontal translation.

Examples