Turning Points of Polynomials

Imagine yourself traveling along the graph of a polynomial, moving from left to right. Sometimes you go ‘uphill’, sometimes ‘downhill’, and sometimes you change direction. Such a change of direction is called a turning point.

The purpose of this section is to make this concept more precise.

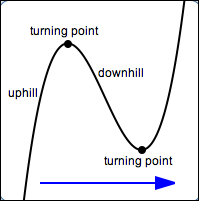
Roughly, a local maximum is a point on a curve where there is a ‘local high spot’. That is, if you ‘stand on’ the point and don't look too far away, then everything you see is lower (or at the same height).

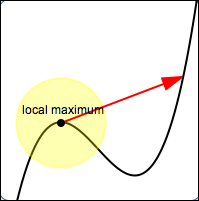
If you look too far away (as the red arrow indicates, above) then you may see points that are higher.

People often say ‘local max’ instead of ‘local maximum’, for brevity.

(The precise definition of a local max is a bit complicated, and is usually covered in a Calculus course.)

There is an analogous description for a local minimum (‘local min’, for short).

Notes about Turning Points

• You ‘turn’ (change directions) at a turning point, so the name is appropriate.

  At a local max, you stop going up, and start going down. At a local min, you stop going down, and start going up.

• For polynomials, a local max or min always occurs at a horizontal tangent line. Thus, a turning point of a polynomial always occurs at a horizontal tangent line.

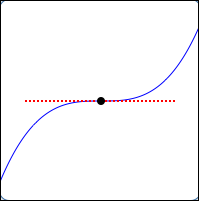
• It's possible to have a horizontal tangent line on a polynomial that is not a turning point, as shown below.

  At the black point below, you don't change direction: you travel uphill to the left of the black point; you also travel uphill to the right of the black point.

A Horizontal Tangent Line that is not a Turning Point

The following fact is easily proved in a Calculus course:

Notes

• Recall:  ‘$\,x\,$ is at most $\,c\,$’ is equivalent to ‘$\,x \le c\,$’. For example, ‘at most $\,3\,$’ means less than or equal to $\,3\,.$
• If you see the graph of a polynomial with (say) $\,5\,$ turning points, then it must have degree at least $\,6\,.$

• Not all numbers less than or equal to $\,n-1\,$ are possible.

  To illustrate, consider the class of cubic (degree $\,3\,$) polynomials. The fact above states that every member of this class has two or fewer turning points.

The polynomial $\,y = x^3\,$ has no turning points.

It has a horizontal tangent line at $\,(0,0)\,,$ which is not a turning point.

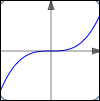
$y = x^3$
no turning points

The polynomial $\,y = x^3 - x\,$ has two turning points.

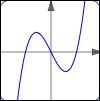
$y = x^3 - x$
two turning points

Does there exist a cubic polynomial with exactly one turning point?

Analysis of end behavior shows that the answer is no, as follows:

• If the leading coefficient of a cubic polynomial is positive, then:

  as $\,x\rightarrow-\infty\,,$  $\,y\rightarrow-\infty$
  as $\,x\rightarrow\infty\,,$  $\,y\rightarrow\infty$

• If the leading coefficient of a cubic polynomial is negative, then:

  as $\,x\rightarrow-\infty\,,$  $\,y\rightarrow\infty$
  as $\,x\rightarrow\infty\,,$  $\,y\rightarrow -\infty$

In both cases, one ‘end’ is going to infinity, and the other to negative infinity.

If a polynomial turns exactly once, then both the right-hand and left-hand end behaviors must be the same. Hence, a cubic polynomial cannot have exactly one turning point.

There does not exist a cubic polynomial with exactly one turning point.

Calculus results about derivatives, together with the Fundamental Theorem of Algebra, will eventually firm up the concepts in this section.