Finding Horizontal Asymptotes

As you age, you grow taller—but not without bound! Eventually, each person settles at a particular height.

Turn off an oven and open up the door—the oven cools down. But it doesn't keep getting colder and colder! Eventually, it settles at room temperature.

Tie an object to the end of a spring, and give it a tug. It bounces ^up and _down, ^up and _down, ^up and _down . Eventually, though, it settles at a particular height.

If you model these real-life scenarios using mathematics, then you'll find yourself dealing with horizontal asymptotes!

As discussed in Introduction to Asymptotes, an asymptote is a curve (usually a line) that another curve gets arbitrarily close to as $\,x\,$ approaches $\,+\infty\,,$ $\,-\infty\,,$ or a finite number.

Here's how this general definition is ‘specialized’ to get a horizontal asymptote:

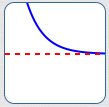
A ‘horizontal asymptote’ is a horizontal line that another curve gets arbitrarily close to as $\,x\,$ approaches $\,+\infty\,$ or $\,-\infty\,.$ (See image below.)

What's the key to a horizontal asymptote situation?

Outputs approach a specific finite number as inputs get arbitrarily large (big and positive, or big and negative).

A situation where something ‘levels out’ or reaches a steady-state is likely to be a situation involving a horizontal asymptote.

This section gives a precise discussion of horizontal asymptotes, as well as conditions under which a rational function has a horizontal asymptote.

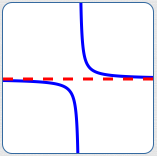
The red line is a horizontal asymptote for the blue curve.

As $\,x\rightarrow\pm\infty\,,$ the blue curve approaches the red line.

That is, as $\,x\rightarrow\pm\infty\,,$ the blue curve outputs approach a specific finite number.

Notes About Horizontal Asymptotes

Equation of a Horizontal Line

Recall that the equation of a horizontal line is ‘$\,y = c\,$’. For example, $\,y = 2\,$ is the horizontal line that crosses the $y$-axis at $\,2\,.$

When asked for a horizontal asymptote, you should give the equation of the desired horizontal line.

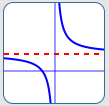
Rational Functions Can Exhibit Horizontal Asymptote Behavior

For example, $\displaystyle\,y = \frac{2x+1}{x}\,$ has horizontal asymptote $\,y = 2\,.$

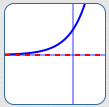
Functions Other Than Rational Functions Can Exhibit Horizontal Asymptote Behavior

For example, $\,y = {\text{e}}^x\,$ has horizontal asymptote $\,y = 0\,.$

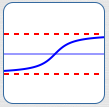
A Function Can Have Exactly One Horizontal Asymptote

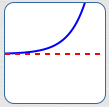
As $\,x\rightarrow -\infty\,,$
$\,y\,$ approaches a finite number

As $\,x\rightarrow \infty\,,$
$\,y\,$ approaches a finite number

As $\,x\rightarrow \pm\infty\,,$
$\,y\,$ approaches the same finite number

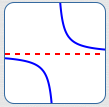
A Function Can Have Two Horizontal Asymptotes

For example, the arctangent function has two horizontal asymptotes, as shown below.

As $\,x\,$ approaches infinity, the $y$-values approach a finite number. As $\,x\,$ approaches negative infinity, the $y$-values approach a different finite number.

A function cannot have more than two horizontal asymptotes.

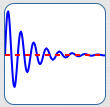
The Graph of a Function Can Cross (Touch) Its Horizontal Asymptote Any Number of Times

For example, the function $\,y = {\text{e}}^{-x}\sin(x)\,$ has horizontal asymptote $\,y = 0\,,$ and its graph crosses this asymptote infinitely many times!

Example 1

Checking a Rational Function For a Horizontal Asymptote: Degree of Denominator Greater Than Degree of Numerator

Let $\displaystyle\,R(x) = \frac{3x-1}{5x^2 + 2x - 1}\,.$

To examine $\,R\,$ for horizontal asymptote behavior, you must understand what the outputs look like when the inputs are very big. More precisely, you must understand what the outputs look like as $\,x\rightarrow\pm\infty\,.$

Let's investigate what happens when $\,x\,$ is big and positive.

As $\,x\rightarrow\infty\,,$ the numerator goes to infinity. (Plug big positive numbers into $\,3x - 1\,.$ ) As $\,x\rightarrow\infty\,,$ the denominator goes to infinity. (Plug big positive numbers into $\,5x^2 + 2x - 1\,.$ )

So, as $\,x\rightarrow\infty\,,$ we have something like looks like $\,\frac{\text{big positive}}{\text{big positive}}\,.$ How useful is this? Not very useful at all!

Let's see if we can rename the function to better understand what happens when $\,x\,$ is big.

The highest power that appears on any $\,x\,$ is $\,\color{red}{2}\,.$ So, the technique we'll use is to multiply both numerator and denominator by $\,\frac{1}{x^{\color{red}{2}}}\,.$ Notice that we're not changing any output values, since we're just multiplying by one!

At first glance, it may look like our renaming has made things more complicated. However, for the purpose of understanding what the outputs look like when $\,x\,$ is big, this is a much better name!

Why? As $\,x\rightarrow\infty\,$ (or as $\,x\rightarrow -\infty\,$), most everything in sight tends to zero!

Therefore, as $\,x\,$ tends to $\,\pm\infty\,,$

So now we know! When $\,x\,$ is big, the outputs are close to zero. Thus, ‘$\,y = 0\,$’ is a horizontal asymptote.

Here's an easier (but less precise) way to think about what is happening:

• The degree of the numerator ($\,3x - 1\,$) is $\,1\,.$
• The degree of the denominator ($\,5x^2 + 2x - 1\,$) is $\,2\,.$
• The degree of the denominator is greater than the degree of the numerator.
• The denominator is getting bigger faster than the numerator.
• This is producing a ‘bottom-heavy’ fraction.
• The fraction is tending to zero!

Example 2

Checking a Rational Function For a Horizontal Asymptote: Degree of Denominator Equal to Degree of Numerator

Let $\displaystyle\,R(x) = \frac{3x-1}{5x + 2}\,.$

Again, as $\,x\rightarrow \infty\,,$ the fraction looks like $\,\frac{\text{big positive}}{\text{big positive}}\,.$   Not very useful in this form!

The highest power that appears on any $\,x\,$ is $\,\color{red}{1}\,$: the technique to use is to multiply both numerator and denominator by  $\,\frac{1}{x^{\color{red}{1}}} = \frac 1x\,.$   No output values are being changed in the following renaming, since we're just multiplying by one!

As $\,x\rightarrow\pm\infty\,,$ both $\,\frac{1}{x}\,$ and $\,\frac{2}{x}\,$ tend to zero. Therefore, as $\,x\,$ tends to $\,\pm\infty\,$:

So now we know! When $\,x\,$ is big, the outputs are close to the finite number $\,\frac{3}{5}\,.$ Thus, ‘$\,y = \frac{3}{5}\,$’ is a horizontal asymptote.

Note that $\,\frac{3}{5}\,$ is the ratio of the leading coefficients of the numerator and denominator:   $\displaystyle\,R(x) = \frac{\boldsymbol{3}x-1}{\boldsymbol{5}x + 2}$

Here's an easier (but less precise) way to think about what is happening:

• The degree of the numerator ($\,3x - 1\,$) is $\,1\,.$
• The degree of the denominator ($\,5x + 2\,$) is $\,1\,.$
• The degree of the denominator is equal to the degree of the numerator.
• Roughly, the numerator and denominator are getting big ‘at the same rates’.
• The outputs approach the ratio of the leading coefficients of the numerator and denominator.

Here's yet another easy (but less precise) way to think about what is happening:

• When inputs are large, a polynomial is well approximated by its highest power term. This highest power term ‘washes out’ the lower-power terms.
• So, when inputs are large, $\,3x - 1\approx 3x\,$ and $\,5x + 2\approx 5x\,\,.$
• So, when inputs are large, $\,\frac{3x-1}{5x-2}\approx \frac{3x}{5x} = \frac{3}{5}\,.$ There's the horizontal asymptote!

In summary, we have:

Conditions Under Which a Rational Function Has a Horizontal Asymptote