 Special Triangles and Common Trigonometric Values
Special Triangles and Common Trigonometric Values
Some students spend hours memorizing tables of common trigonometric values, like (say) $\,\sin 30^\circ = \frac 12\,$ and $\,\cos 45^\circ = \frac 1{\sqrt 2} = \frac{\sqrt{2}}2\,.$ Don't do this! Spend your time in more useful and enjoyable ways!
With just two special triangles, and the right triangle and unit circle approaches, all the common trigonometric values are at your fingertips.
The $\,30^\circ{-}60^\circ{-}90^\circ\,$ and $\,45^\circ{-}45^\circ{-}90^\circ\,$ triangles were introduced in Two Special Triangles. For finding trigonometric values, any size triangle will work—make the shortest side(s) length $\,1\,$ to get the simplest numbers (see below). Memorize (just) these two triangles, and study the examples below for the needed techniques.
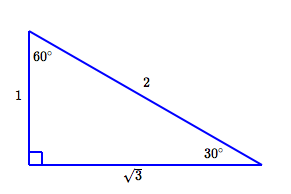
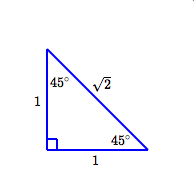
Trigonometric Values for $\,30^\circ\,,$ $\,45^\circ\,,$ and $\,60^\circ$
Whenever you need the sine, cosine or tangent of $\,30^\circ\,,$ $\,45^\circ\,$ or $\,60^\circ\,,$ use these special triangles and (if necessary) the memory device ‘SOHCAHTOA’ (pronounced ‘sew-ca-toe-uh’):
Sine Opposite Hypotenuse Cosine Adjacent Hypotenuse Tangent Opposite Adjacent
SINE COSINE TANGENT
| $30^\circ$ | $\displaystyle\sin 30^\circ = \frac{\text{OPP}}{\text{HYP}} = \frac 12$ |
| $\displaystyle\cos 30^\circ = \frac{\text{ADJ}}{\text{HYP}} = \frac{\sqrt 3}2$ | |
| $\displaystyle\tan 30^\circ = \frac{\text{OPP}}{\text{ADJ}} = \frac1{\sqrt 3} = \frac{\sqrt 3}{3} $ |
| $45^\circ$ | $\displaystyle\sin 45^\circ = \frac{\text{OPP}}{\text{HYP}} = \frac 1{\sqrt 2} = \frac{\sqrt 2}{2}$ |
| $\displaystyle\cos 45^\circ = \frac{\text{ADJ}}{\text{HYP}} = \frac 1{\sqrt 2} = \frac{\sqrt 2}{2}$ | |
| $\displaystyle\tan 45^\circ = \frac{\text{OPP}}{\text{ADJ}} = \frac{1}{1} = 1$ |
| $60^\circ$ | $\displaystyle\sin 60^\circ = \frac{\text{OPP}}{\text{HYP}} = \frac{\sqrt 3}{2}$ |
| $\displaystyle\cos 60^\circ = \frac{\text{ADJ}}{\text{HYP}} = \frac{1}{2}$ | |
| $\displaystyle\tan 60^\circ = \frac{\text{OPP}}{\text{ADJ}} = \frac{\sqrt 3}{1} = \sqrt 3$ |
Which Name to Use: $\,\displaystyle\frac{1}{\sqrt 2}\,$ or $\,\displaystyle\frac{\sqrt 2}{2}\,$?
You'll notice that two different names are given in the tables above for some of the trigonometric values—those that initially have a square root in the denominator.
For example, the number $\,\frac{1}{\sqrt 2}\,$ has a radical in the denominator, so a second name is offered: $\frac{1}{\sqrt 2} = \frac{\sqrt 2}{2}\,.$
The process of going from the name $\,\frac{1}{\sqrt 2}\,$ to the name $\,\frac{\sqrt 2}2\,$ is called ‘rationalizing the denominator’, which means to ‘get rid of the radical in the denominator’.
The radical doesn't disappear—it just moves up to the numerator. It's a beautiful application of ‘multiplying by $\,1\,$ in an appropriate form’:
$$ \cssId{s38}{\frac 1{\sqrt 2}} \ \ \cssId{s39}{=\ \ \frac 1{\sqrt 2}\cdot\frac{\sqrt 2}{\sqrt 2}} \ \ \cssId{s40}{=\ \ \frac{\sqrt 2}{2}} $$So, which name should you use? It depends!
There are computational advantages to the name $\,\frac{\sqrt 2}{2}\,$ when hand or slide rule calculations are being done, which justifies the historical renaming preference. With modern computers and calculators, that advantage is long gone.
I zipped up to wolframalpha.com to see if it produced any difference at all between the two names (perhaps in those far-right decimal places), but it didn't:
| $\displaystyle\frac{\sqrt 2}{2}$ |
 |
| $\displaystyle\frac1{\sqrt 2}$ |
 |
Old habits often die hard. For example, I'm quite certain the words ‘clockwise’ and ‘counterclockwise’ will hang around, even though it's already rare to see a clock with rotating hands.
Some teachers may like (and insist upon) the consistency of always getting the same ‘name’ for an answer. Most text books still insist upon rationalizing the denominator to match the answers in the back of the book.
So, your teacher may require that you get rid of any radicals in the denominator. For this web site, however, answers are usually reported as they arise naturally in problem-solving, and are not renamed unless there is a compelling reason to do so.
Trigonometric Values For Arbitrary Special Angles (Including Multiples of $\,30^\circ\,$ and $\,45^\circ\,$)
By combining the special triangles with the unit circle approach, you have easy access to special angles in all four quadrants.
The next example illustrates the technique by finding the trigonometric values of $\,330^\circ\,.$ The three basic steps are LOCATE, SHRINK/SIZE, and SIGNS.
LOCATE:
Lay off the desired (special) angle. Recall that positive angles are swept out in a counterclockwise direction; start by going up. Negative angles are swept out in a clockwise direction; start by going down.
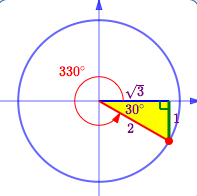
Drop a perpendicular from the terminal point to the $x$-axis. Of course, it really isn't the terminal point until the triangle is ‘shrunk’ in the next step. But, you know what I mean!
Notice how a special triangle appears! Label the (acute) angle between the $x$-axis and hypotenuse, and the (memorized) lengths of the sides.
SHRINK/SIZE:
‘Shrink’ the triangle so it fits in the unit circle, by dividing all the sides by the hypotenuse . The leg lengths now give the correct size of the coordinates of the terminal point, but the signs may be wrong.
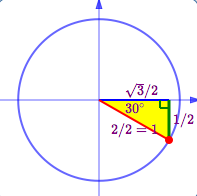
SIGNS:
Determine the correct signs (plus or minus) of the $x$-value and $y$-value of the terminal point. Review Locating Points in Quadrants and On Axes as needed.
The most common mistake is getting the wrong sign! To prevent this error, write down the sign ($\pm$) first, then write the correct size.
The statement above about the ‘terminal point’ not really being the terminal point brought to mind something I've said many times during my lectures over three decades of teaching. Not quite sure where I picked it up, or who I got it from, but it goes like this:
If I say it correctly and write it incorrectly,
then believe what I say.
If I say it incorrectly and write it correctly,
then believe what I write.
If I say it incorrectly and write it incorrectly,
then—well, you know what I meant anyway!