Logarithmic Functions: Review and Additional Properties
A logarithmic function is a function of the form $\,f(x) = \log_b x\,$ for $\,b \gt 0\,$ and $\,b\ne 1\,.$
‘log base $\,b\,$ of $\,x\,$’
‘$\,\log_b\,$’ (read aloud as ‘log base $\,b\,$’) is the name of the function, and it acts on the input $\,x\,.$
When there's no confusion about order of operations, mathematical convention dictates that we can drop the parentheses used to ‘hold’ the input, and write ‘$\,\log_b x\,$’ (without parentheses) instead of the more cumbersome ‘$\,\log_b(x)\,$’.
If order of operations becomes ambiguous, be sure to include parentheses for clarification. Thus, for example, you should write either $\,\log_b(x + 1)\,$ or $\,(\log_b x) + 1\,,$ but never the ambiguous ‘$\,\log_b x + 1\,$’. (Notice, however, that there is no ambiguity in the expression ‘$\,1 + \log_b x\,$’.)
The number $\,b\,$ in $\,\log_b x \,$ is called the base of the logarithm.
When the base is $\,\text{e}\,,$ the function is called the natural logarithm, and can be written as $\,y = \ln x\,.$ (Note: $\text{e}\approx 2.71828\,$)
When the base is $\,10\,,$ the function is called the common logarithm, and can be written as $\,y = \log x\,.$
Logarithmic functions and their graphs were introduced in the Algebra II curriculum:
- Thoroughly study this earlier section: Introduction to Logarithmic Functions
- Print out an 18-question worksheet to make sure you've mastered all the different problem types.
Additional higher-level information that is important for Precalculus is presented below.
Increasing/Decreasing Properties of Logarithmic Functions
Increasing Logarithmic Functions
When $\,b \gt 1\,,$ $\,f(x) = \log_b x\,$ is an increasing function. That is, for all positive real numbers $\,x\,$ and $\,y\,$:
$$ \cssId{s23}{x \lt y \ \ \Rightarrow\ \ \log_b x \lt \log_b y} $$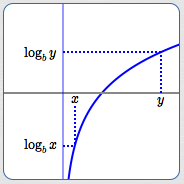
It is clear from the graph that the other direction is also true:
$$ \cssId{s25}{\log_b x \lt \log_b y \ \ \Rightarrow\ \ x \lt y} $$Together, we have that for all positive real numbers $\,x\,$ and $\,y\,,$ and for $\,b \gt 1\,$:
Notice that when the base of the logarithm is greater than one, the inequality symbols that compare the inputs ($\,x\,$ and $\,y\,$) and their corresponding outputs ($\,\log_b x\,$ and $\,\log_b y\,$) have the same direction:
This equivalence can be alternatively stated as:
$y = \log_b x\,,$
for $\,b \gt 1\,$
An increasing
logarithmic function
$x \lt y \ \iff\ \log_b x \lt \log_b y$
Decreasing Logarithmic Functions
When $\,0 \lt b \lt 1\,,$ $\,f(x) = \log_b x\,$ is a decreasing function. That is, for all positive real numbers $\,x\,$ and $\,y\,$:
$$ \cssId{s40}{x \lt y \ \ \Rightarrow\ \ \log_b x \gt \log_b y} $$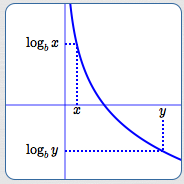
It is clear from the graph that the other direction is also true:
$$ \cssId{s42}{\log_b x \gt \log_b y \ \ \Rightarrow\ \ x \lt y} $$Together, we have that for all positive real numbers $\,x\,$ and $\,y\,,$ and for $\,0 \lt b \lt 1\,$:
Notice that when the base of the logarithm is between zero and one, the inequality symbols that compare the inputs ($\,x\,$ and $\,y\,$) and their corresponding outputs ($\,\log_b x\,$ and $\,\log_b y\,$) have different directions:
This equivalence can be alternatively stated as:
$y = \log_b x\,,$
for $\,0 \lt b \lt 1\,$
A decreasing
logarithmic function
$x \lt y \ \iff\ \log_b x \gt \log_b y$
Logarithmic Functions are One-to-One
The graphs of logarithmic functions pass both vertical and horizontal lines tests, so they are one-to-one functions. Thus, for all positive real numbers $\,x\,$ and $\,y\,$:
Consequently, logarithmic functions have inverses.
Logarithmic Functions and Exponential Functions are Inverses
Logarithmic functions and exponential functions with the same bases are inverses—they ‘undo’ each other. Roughly:
- If the exponential function with base ‘$\,a\,$’ does something, then the logarithmic function with base ‘$\,a\,$’ undoes it.
- If the logarithmic function with base ‘$\,a\,$’ does something, then the exponential function with base ‘$\,a\,$’ undoes it.
These relationships are firmed up mathematically below.
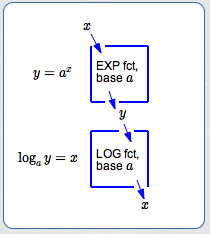
Drop $\,x\,$ in the ‘exponential function with base $\,a\,$’ box; get $\,y\,$ out the bottom. (See the top box in the diagram above.) This is expressed mathematically as:
$$\cssId{s71}{y = a^x}$$Drop $\,y\,$ in the ‘logarithmic function with base $\,a\,$’ box; get $\,x\,$ out the bottom. (See the bottom box in the diagram above.) This is expressed mathematically as:
$$\cssId{s76}{\log_a y = x}$$Since the exponential and logarithmic functions with base $\,a\,$ are inverses, these two operations are equivalent:
$$\cssId{s78}{y = a^x\ \ \iff\ \ \log_a y = x}$$If one is true, so is the other. If one is false, so is the other. They are true and false at the same time. In other words:
- If the exponential function with base $\,a\,$ takes $\,x\,$ to $\,y\,,$ then the logarithmic function with base $\,a\,$ takes $\,y\,$ back to $\,x\,.$
- If the logarithmic function with base $\,a\,$ takes $\,y\,$ to $\,x\,,$ then the exponential function with base $\,a\,$ takes $\,x\,$ back to $\,y\,.$
‘$\,y = a^x\,$’ is called the exponential form of the equation.
‘$\log_a y = x\,$’ is called the logarithmic form of the equation.
The exponential and logarithmic functions with the same bases ‘undo’ each other!
When
‘EXP fct, base $\,a\,$’
takes $\,x\,$ to $\,y\,,$
then
‘LOG fct, base $\,a\,$’
takes $\,y\,$ back to $\,x\,.$
Read-Through, Part 2
Going from Logarithmic Form to Exponential Form
Going from logarithmic form ‘$\,\log_a y = x\,$’ to the equivalent exponential form ‘$\,y = a^x\,$’ is easy! Start with the base ‘$\,a\,$’, circle counterclockwise to $\,x\,,$ and then to $\,y\,$:
This circular motion actually gives ‘$\,a^x = y\,$’. Then, write it again from right-to-left to get ‘$\,y = a^x\,$’ !
Going from Exponential Form to Logarithmic Form
Here's a thought process to go from exponential form ‘$\,y = a^x\,$’ to the equivalent logarithmic form ‘$\,\log_a y = x\,$’:
- We want a logarithmic form, so start by writing: $\,\color{red}{\log}$
- The base of the logarithm is the same as the base of the exponential function, so add in the base: $\,\color{red}{\log_a}$
-
A logarithm is an exponent! The word ‘is’ translates as ‘$\,=\,$’.
The only exponent in ‘$\,y = a^x\,$’ is $\,x\,.$
Leaving a space for the input, add in ‘$\,= x\,$’: $$\color{red}{\log_a\ \ \ = x}$$
-
There's only one variable left in ‘$\,y = a^x\,$’ , and only one place to put it!
Finish by putting in the ‘$\,y\,$’ : $$\color{red}{\log_a y= x}$$
Domain/Range Considerations for Logarithmic and Exponential Functions
Let $\,a \gt 0\,,$ $\,a \ne 1\,.$ These are the allowable bases for logarithmic and exponential functions.
For exponential functions, $\,y = a^x\,$:
- the domain is the set of all real numbers
- the range is the set of positive real numbers
For logarithmic functions, $\,y = \log_a x\,$:
- the domain is the set of positive real numbers
- the range is the set of all real numbers
Observe that:
- the domain of $\,y = a^x\,$ is the range of $\,y = \log_a x\,$
- the range of $\,y = a^x\,$ is the domain of $\,y = \log_a x\,$
The input/output sets for inverses are switched! The input set for one is the output set for the other. The output set for one is the input set for the other.
Two Important Views of Logarithms
Now, you should be comfortable with both important views of logarithms:
-
A Logarithm Is An Exponent: What is $\,\log_a x\,$?
It is the power (the exponent) that ‘$\,a\,$’ must be raised to, in order to get $\,x\,.$
-
Logarithms ‘Undo’ Exponents: If the exponential function with base $\,a\,$ takes input $\,x\,$ to output $\,y\,,$ then what function takes $\,y\,$ back to $\,x\,$?
Answer: the logarithmic function with base $\,a\,$
Solving Inequalities Involving Logarithmic Functions
Equivalences (1), (2), and (3) can be used to solve certain types of mathematical sentences involving logarithms, as illustrated in the following examples.
IMPORTANT: Whenever you have an expression of the form ‘$\,\log_a (\text{stuff})\,$’, the ‘stuff ’ must be positive!
Example 1
SOLVE:
$$ \cssId{sb47}{\log_2(3x-1) \lt \log_2(5x)} $$This is an inequality of the form
$$\cssId{sb49}{\log_b(\text{stuff1}) \lt \log_b(\text{stuff2})}$$where the base of the logarithm, $\,b\,,$ is $\,2\,.$
Notice that the logarithmic functions on both sides use the same base.
In this example, the base is greater than one, so we'll use equivalence $(1)$:
$$\cssId{sb53}{x \lt y \ \ \iff\ \ \log_b x \lt \log_b y}$$SOLUTION:
Since logarithms only act on positive numbers, we must also have:
Putting everything together:
The solution set of this inequality is:
$$ \cssId{sb61}{\underbrace{\{x\ |\ x > \frac 13\}}_{\text{set-builder notation}} = \underbrace{(\frac 13,\infty)}_{\text{interval notation}}} $$
Blue curve: $y = \log_2 (3x - 1)$
Red curve: $y = \log_2 (5x)$
The blue curve is only defined for $\,x \gt \frac 13\,.$
The blue curve lies below the red curve
everywhere that it
is defined.
Head up to wolframalpha.com and type in:
log_2 (3x -1) < log_2 (5x)
Voila!
Example 2
SOLVE:
$$ \cssId{sb71}{\log_{0.3}(7) - \log_{0.3}(1 - 6x) \gt 0} $$This is an inequality that can be easily transformed to
$$\cssId{sb73}{\log_b(\text{stuff1}) > \log_b(\text{stuff2})}$$where the base of the logarithm, $\,b\,,$ is $\,0.3\,.$ Notice that the logarithmic functions use the same base.
In this example, the base is between zero and one, so we'll use equivalence $(2)$:
$$\cssId{sb77}{x \lt y \ \ \iff\ \ \log_b x \gt \log_b y}$$Compare the solution below to what you get at wolframalpha.com:
log_(0.3) (7) - log_(0.3) (1 - 6x) > 0
SOLUTION:
Here are the reasons for each step:
- Original inequality
- Addition property for inequalities
- Equivalence $(2)$—inequality symbol changes direction; inputs to logs must be positive
- Addition property for inequalities
- Multiplication property for inequalities
-
How can a number be both less than $\,-1\,$ and less than $\,\frac 16\,$ at the same time?
Answer: By being less than $\,-1\,$!
Notice in the third step that the inequality symbol changed direction, since equivalence $(2)$ is being used.
Example 3
SOLVE:
$$ \cssId{sb94}{\ln(2x + 1) = \ln(7x - 3)} $$Here's a screenshot from wolframalpha.com:
Writing a list of equivalent mathematical sentences: