audio read-through Solving Exponential Growth and Decay Problems

This section presents a variety of problems, utilizing ideas and techniques covered in:

Once you've recognized exponential behavior (equal changes in the input cause the output to be multiplied by a constant) then you can always use $\,P(t) = P_{0}{\text{e}}^{rt}\,$ as your model. However, it is often more natural and easier to use a different base.

Examples

Initial Population and Relative Growth Rate Given; Find a Future Population Size

Example:  Suppose the population of a city was $\,680{,}000\,$ in $\,1992$; the relative growth rate is $\,12\%\,$ per year. What is the population $\,t\,$ years after $\,1992$? In the year $\,2000$?

Let $\,t = 0\,$ in $\,1992\,,$ and measure $\,t\,$ in years.

Choose $\,t = 0\,.$ Here, the year corresponding to the earliest known population size is chosen.

Since the given relative growth rate is ‘$\,12\%\,$ per year’, you need to use units of ‘year’ for time when using the model $\,P(t) = P_{0}{\text{e}}^{rt}\,.$

Let $\,P(t)\,$ have units of thousands.

For example, $\,P(t) = 680\,$ means that the population at time $\,t\,$ is $\,680{,}000\,.$

Choose the units for the output. By using units of thousands, you can work with smaller numbers.

Let $\,P(t) = P_{0}{\text{e}}^{rt}\,,$ where:

  • $\,r = \text{the relative growth rate} = 12\% = 0.12\,$ per year
  • $P_{0} = \text{the population at time zero} = 680\,$

Thus, $\,P(t) = 680{\text{e}}^{0.12t}\,$ gives the population $\,t\,$ years after $\,1992\,.$

Whenever you see the phrase relative growth rate, continuous growth rate, or exponential growth rate, you know you're dealing with exponential behavior.

As discussed in Exponential Growth and Decay: Introduction, all exponential growth/decay problems can be modeled using $\,P(t) = P_{0}{\text{e}}^{rt}\,,$ where $\,r\,$ is the relative growth rate.

The year $\,2000\,$ corresponds to:

$\,t = 2000-1992 = 8\,$

$P(8) = 680{\text{e}}^{(0.12)(8)} \approx 1775.954\,$

In the year $\,2000\,,$ the population will be about $\,1{,}775{,}954\,$ people.

Be careful with units! Here, $\,P(8) \approx 1775.954\,$ has units of thousands. Thus, the output of $\,1775.954\,$ from the function $\,P\,$ corresponds to a population of $\,(1775.954)(1000) = 1{,}775{,}954\,.$

Be Careful! These are not the same thing!

‘A relative growth rate of $\,12\%\,$ per year’

‘Growing at the rate of $\,12\%\,$ per year’ (an annual growth rate)

As the next example shows, an annual growth rate of $\,12\%\,$ corresponds to a relative growth rate of approximately $\,11.33\%\,$ per year.

Initial Population and Annual Growth Rate Given; Find a Future Population Size

Example:  Suppose the population of a city was $\,680{,}000\,$ in $\,1992$; it is growing at the rate of $\,12\%\,$ per year. What is the population $\,t\,$ years after $\,1992$? In the year $\,2000$?

Let $\,t = 0\,$ in $\,1992\,,$ and measure $\,t\,$ in years.
Choose $\,t = 0\,$ and units for the input.
Let $\,P(t)\,$ have units of thousands.
Choose the units for the output.

Recognize exponential growth: equal changes in the input (every year) cause the output to be multiplied by a constant ($\,1.12\,$).

Let $\,P(t) = P_{0}{\text{e}}^{rt}\,,$ where:

  • $P_{0} = \text{the population at time zero} = 680\,$
  • We must find the relative growth rate, $\,r\,$
After one year, the population is: $$ \begin{align} &P_{0} + (12\%)(P_{0})\cr &\quad = 1\,P_{0} + (0.12)(P_{0})\cr &\quad = 1.12P_{0} \end{align} $$

A growth rate of $\,12\%\,$ per year corresponds to a yearly multiplier of $\,1.12\,.$

Once exponential behavior has been identified, you can always use the model $\,P(t) = P_{0}{\text{e}}^{rt}\,.$ However, it is not always easiest.

Exponential behavior is defined by equal changes in the input causing the output to be multiplied by a constant. Whenever an (equal change,constant multiplier) pair is known, then there is a more natural exponential model to use, as shown below.

Use $\,P(1) = (1.12)P_{0}\,$ to solve for $\,r\,$:

$\overbrace{P_{0}\,{\text{e}}^{r\cdot 1}}^{P(1)} = 1.12P_{0}$

${\text{e}}^r = 1.12$   (divide by $\,P_{0}\,$)

$r = \ln 1.12$

Thus:

$\,P(t) = 680{\text{e}}^{t\ln 1.12}\,$

$\,P(8) = 680{\text{e}}^{8\cdot \ln 1.12} \approx 1683.655\,$

In the year $\,2000\,,$ the population will be about $\,1{,}683{,}655\,$ people. (An annual growth rate of $\,12\%\,$ is slightly slower than a relative growth rate of $\,12\%\,.$ )

Notice that an annual growth rate of $\,12\% = 0.12\,$ corresponds to a relative growth rate of: $$\ln 1.12 \approx 0.1133 = 11.33\%$$

Similarly, an annual growth rate of $\,g\,$ corresponds to a relative growth rate of $\,\ln(1 + g)\,.$

The graph below shows the annual growth rate in blue, and the relative growth rate in red. For growth rates up to about $\,5\%\,$ they are almost indistinguishable. (Note: the horizontal axis is $\,g\,.$)

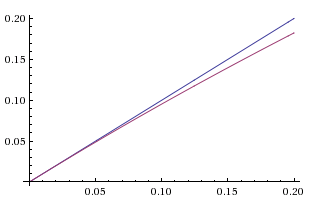
annual growth rate versus relative growth rate

$\,y = g\,$ (blue)
$\,y = \ln (1 + g)\,$ (red)

Alternative Solution (Easiest)

Let $\,t = 0\,$ in $\,1992\,,$ and measure $\,t\,$ in years.

Let $\,P(t)\,$ have units of thousands.

Then:

$\,P(t) = 680(1.12)^t\,$

$\,P(8) = 680(1.12)^8 \approx 1683.655\,$
(Of course, this is the same answer as above!)

Much easier!

Looking at a few years of population, a pattern quickly emerges:

$t = 0$$P(0) = 680 = 680t^0$
$t = 1$$P(1) = 680(1.12) = 680(1.12)^1$
$t = 2$$P(2) = 680(1.12)^2$
$t$$P(t) = 680(1.12)^t$

So, even though you always have the option of using the exponential model $\,P(t) = P_{0}{\text{e}}^{rt}\,,$ it is not always in your best interest to do so!

More Alternative Solutions

Different choices (for time zero, for input/output units) will cause the solution steps to look different. As long as you're consistent with your choices, though, you'll always end up at exactly the same place!

To illustrate, here are a couple more ways of doing the previous problem. These are not recommended choices—they just illustrate possibilities.

The problem is repeated here for your convenience: Suppose the population of a city was $\,680{,}000\,$ in $\,1992$; it is growing at the rate of $\,12\%\,$ per year. What is the population $\,t\,$ years after $\,1992$? In the year $\,2000$?

(First Alternative Solution: Not Recommended!)

Let $\,t = 0\,$ in $\,2000\,,$ and measure $\,t\,$ in years.

Let $\,P(t) = P_{0}{\text{e}}^{rt}\,$; both $\,P_{0}\,$ and $\,r\,$ must be found.

Since $P(1) = (1.12)P(0)$:

$$ \begin{gather} \cssId{s112}{P_{0}{\text{e}}^r = (1.12)P_{0}}\cr \,\cssId{s113}{r = \ln (1.12)} \end{gather} $$

Since $P(-8) = 680{,}000\,$:

$$ \cssId{s115}{P_{0}{\text{e}}^{-8\ln(1.12)} = 680{,}000} $$ $$ \begin{align} P_{0}\ &\cssId{s116}{= \frac{680{,}000}{ {\text{e}}^{-8\ln(1.12)} } }\cr\cr &\cssId{s117}{= \frac{680{,}000}{1.12^{-8}}}\cr\cr &\cssId{s118}{= 680{,}000(1.12)^8}\cr\cr &\cssId{s119}{\approx 1{,}683{,}655} \end{align} $$ Note that $\,P_{0}\,$ is the population in the year $\,2000\,.$

The population $\,t\,$ years after $\,1992\,$ (which is $\,t-8\,$ years after $\,2000\,$) is: $$\cssId{s123}{P(t-8) = 1{,}683{,}655{\text{e}}^{(t-8)\ln(1.12)}}$$

(Second Alternative Solution: Not Recommended!)

Let $\,t = 0\,$ in $\,1992\,,$ and measure $\,t\,$ in weeks.

Let $\,P(t)\,$ have units of hundred-thousands.

Then $\,P(t) = 6.8{\text{e}}^{rt}\,$; $\,r\,$ must be found.

Since $P(52) = (1.12)P(0)\,$:

$$ \begin{gather} \cssId{s129}{P_{0}{\text{e}}^{52r} = (1.12)P_{0}}\cr\cr \cssId{s130}{52r = \ln (1.12)}\cr\cr \cssId{s131}{r = \frac{\ln(1.12)}{52}} \end{gather} $$

So:

$$\cssId{s133}{P(t) = 6.8\ {\text{e}}^{t\ln(1.12)/52}}$$

Finally:

$$ \cssId{s135}{P(8\cdot 52) = 6.8\ {\text{e}}^{8\cdot 52\cdot \ln(1.12)/52} \approx 16.83655} $$

Therefore, the population in the year $\,2000\,$ is:

$$\cssId{s137}{(16.83655)(100{,}000) = 1{,}683{,}655}$$

Yuck!  These are certainly not good choices to make for this problem!

(Equal Change,Constant Multiplier) Pair Known

Exponential behavior is defined by equal changes in the input causing the output to be multiplied by a constant. Whenever an (equal change,constant multiplier) pair is known, then there is a natural exponential model to use, as discussed next.

Suppose that a time change of $\,\Delta t\,$ (read as ‘delta $\,t\,$’) causes the output to successively be multiplied by a constant $\,b\,.$ Thus, we are considering the (equal change,constant multiplier) pair to be $\,(\Delta t,b)\,.$

Letting $\,P_{0}\,$ denote the starting amount and $\,P(t)\,$ the amount at time $\,t\,,$ a pattern quickly emerges:

Starting amount:  amount at $\,t = 0$ $P(0) = P_{0} = P_{0}b^0$
Amount at time $\Delta t$

(one time period elapses)

 Prior amount gets multiplied by $\,b$ $\begin{align} P(\Delta t) &= b\cdot P_{0}b^0\cr &= P_{0}b^1 \end{align}$
Amount at time $2\Delta t$

(another time period elapses) 		Prior amount gets multiplied by $\,b$ $\begin{align} P(2\Delta t) &= b\cdot P_{0}b^1\cr &= P_{0}b^2 \end{align}$
Amount at time $3\Delta t$

(another time period elapses)		 Prior amount gets multiplied by $\,b\,$ $\begin{align} P(3\Delta t) &= b\cdot P_{0}b^2\cr &= P_{0}b^3 \end{align}$

In general, we have $\,P(\color{red}{k\Delta t}) = P_{0}b^{k}\,.$ But, what is the amount at an arbitrary time $\,t\,$?

Let $\,t = \color{red}{k\Delta t}\,,$ so that $k = t/\Delta t\,.$ Then we have:

$$\cssId{s163}{\large P(t) = P_{0}\,b^{t/\Delta t}}$$

is an exponential model corresponding to an (equal change,constant multiplier) pair $\,(\Delta t,b)\,$ and initial amount $\,P_{0}$

Note that:

  • The constant multiplier becomes the base of the exponential function.
  • In the exponent, time gets divided by the ‘equal change’.

Here are examples:

First Example

Suppose something doubles every $\,3\,$ seconds. ‘Doubling’ is multiplying by $\,2\,.$

Then, the (equal change,constant multiplier) pair is $\,(3,2)\,.$

The model is

$$P(t) = P_{0}\,2^{t/3}\,,$$ where $\,t\,$ is measured in seconds.

Second Example

Suppose something gets halved every $\,7\,$ minutes. ‘Halving’ is multiplying by $\,0.5\,.$

Then, the (equal change,constant multiplier) pair is $\,(7,0.5)\,.$

The model is

$$P(t) = P_{0}(0.5)^{t/7}\,,$$ where $\,t\,$ is measured in minutes.

A variety of other names are possible:

$$ \begin{align} P(t)\ &\cssId{s180}{=\ P_0 (0.5)^{t/7}}\cr\cr &\cssId{s181}{=\ P_0 \bigl(\frac 12\bigr)^{t/7}}\cr\cr &\cssId{s182}{=\ \frac{P_0}{2^{t/7}}}\cr\cr &\cssId{s183}{=\ P_0\, 2^{-t/7}}\cr\cr &\cssId{s184}{=\ \cdots} \end{align} $$

Non-Uniqueness of (equal change,constant multiplier ) Pair

Note:  An (equal change,constant multiplier) pair is not unique! If $\,(\Delta t,b)\,$ is such a pair, then so is $\displaystyle\,(k\Delta t,b^k)\,$ for every nonzero real number $\,k\,,$ since: $$ \begin{align} P(t)\ &\cssId{s188}{= P_{0}(b^k)^{\frac{t}{k\Delta t}}}\cr\cr &\cssId{s189}{= P_{0}\,b^{k\,\cdot\,\frac{t}{k\Delta t}}}\cr\cr &\cssId{s190}{= P_{0}\,b^{t/\Delta t}} \end{align} $$

Concept Practice