Inverse Trigonometric Function: Arcsine (Part 2)

(This page is Part 2. Click here for Part 1.)

Formal Name Versus Function Notation Abbreviations

The formal name of the function being discussed in this section is ‘arcsine’. It has an ‘e’ on the end, and is pronounced ARC-sine (with a long ‘i’ in ‘sine’).

When using function notation, ‘arcsine’ is abbreviated as ‘$\,\arcsin\,$’. It has no ‘e’ on the end, but is pronounced the same as ‘arcsine’. Thus, ‘$\,\arcsin x\,$’ is read aloud as ‘arcsine of $\,x\,$’.

An alternative notation for the arcsine function is ‘$\,\sin^{-1}\,$’. This alternative notation is modeled on the standard notation for inverse functions: if $\,f\,$ is one-to-one, then its inverse is called $\,f^{-1}\,.$

The function notation ‘$\,\sin^{-1} x\,$’ can be read aloud as ‘arcsine of $\,x\,$’ or ‘the inverse sine of $\,x\,$’. DON'T read ‘$\,\sin^{-1} x\,$’ as ‘sine to the negative one of $\,x\,$’! There is no reciprocal operation going on here—it's just standard notation for an inverse function.

Convention for Multi-Letter Function Names

Since both ‘$\,\arcsin\,$’ and ‘$\,\sin^{-1}\,$’ are multi-letter function names, the standard convention applies: the parentheses that typically hold the input can be removed, if there is no possible confusion about order of operations.

Thus, you usually see  ‘$\,\arcsin x\,$’  and  ‘$\,\sin^{-1} x\,$’  (no parentheses), instead of the more cumbersome  ‘$\,\arcsin (x)\,$’  and  ‘$\,\sin^{-1} (x)\,$’  (with parentheses).

Function Name Versus Output From the Function

The function name is ‘$\,\arcsin\,$’. The number ‘$\,\arcsin x\,$’ is the output from the function ‘$\,\arcsin\,$’ when the input is $\,x\,.$

Similarly, the function name is ‘$\,\sin^{-1}\,$’. The number ‘$\,\sin^{-1} x\,$’ is the output from the function ‘$\,\sin^{-1}\,$’ when the input is $\,x\,.$

Preferred Notation

Since the sine function does not have a true inverse, this author believes the notation ‘$\,\sin^{-1}\,$’ is misleading and lends itself to errors. This author strongly prefers the notation ‘$\,\arcsin\,$’.

Alternate Definition, Using Degrees Instead of Radians

Inputs to trigonometric functions can be viewed as real numbers (radian measure) or degrees.

For example, $\,\sin \frac{\pi}{2} = 1\,$:  here, $\,\frac{\pi}{2}\,$ is radian measure.

Equivalently, $\,\sin 90^\circ = 1\,$:  here, $\,90^\circ\,$ is degree measure.

Here's what the definition of arcsine looks like, using degree measure instead of radian measure:

Calculator Skills

If a calculator is in degree mode, then $\,\arcsin x\,$ is reported in degrees. If a calculator is in radian mode, then $\,\arcsin x\,$ is reported in radians.

Graph of the Arcsine Function

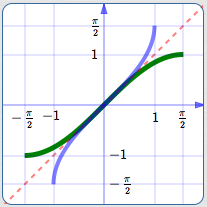
For a one-to-one function $\,f\,,$ the graph of its inverse, $\,f^{-1}\,,$ is found by reflecting the graph of $\,f\,$ about the line $\,y = x\,.$ Below, this technique is used to construct the graph of the arcsine function:

Here's the piece of the sine curve that is used to define the arcsine function:

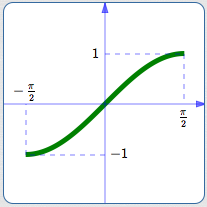
Domain:  $\,[-\frac{\pi}{2},\frac{\pi}{2}]$

Range:  $\,[-1,1]$

Here's the same curve, together with its reflection about the line $\,\color{red}{y = x}$

The Graph of the Arcsine Function

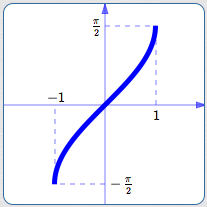
Domain:  $\,[-1,1]$

Range:  $\,[-\frac{\pi}{2},\frac{\pi}{2}]$

Notice that the domain and range of a function and its inverse are switched! The domain of one is the range of the other. The range of one is the domain of the other.

Relationship Between the Sine and Arcsine Functions

For a one-to-one function $\,f\,$ and its inverse $\,f^{-1}\,,$ there is a simple ‘undoing’ relationship between the two:

• $f^{-1}\bigl(f(x)\bigr) = x\,$ for all $\,x\,$ in the domain of $\,f\,$:  the function $\,f\,$ does something, and $\,f^{-1}\,$ undoes it
• $f\bigl(f^{-1}(x)\bigr) = x\,$ for all $\,x\,$ in the range of $\,f\,$:   the function $\,f^{-1}\,$ does something, and $\,f\,$ undoes it

Since the sine and arcsine functions are not true inverses of each other, the relationship between them is a bit more complicated.

The Direction Where Sine and Arcsine ‘Undo’ Each Other Nicely

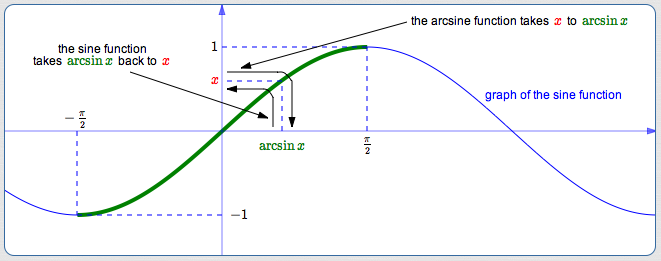
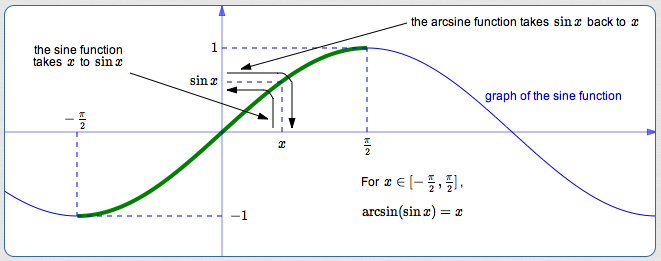
Here's the direction where they do ‘undo’ each other nicely:   Start with a number, first apply the arcsine function, then apply the sine function, and end up right where you started.

Here are the details:  For all $\,x\in [-1,1]\,,$

• Start with $\,\color{red}{x}\in [-1,1]$
• The arcsine function takes $\,\color{red}{x}\,$ to $\,\color{green}{\arcsin x}\,$ in the interval $\,[-\frac{\pi}2,\frac{\pi}2]$
• The sine function takes $\,\color{green}{\arcsin x}\,$ back to $\,\color{red}{x}$

The Direction Where Sine and Arcsine Don't Necessarily ‘Undo’ Each Other Nicely

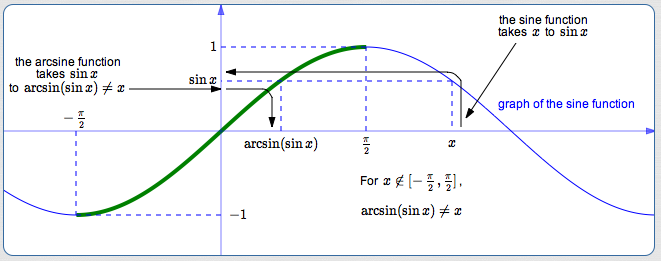
Here's the direction where they don't necessarily ‘undo’ each other nicely. Start with a number, first apply the sine function, then apply the arcsine function. If the number you started with is outside the interval $\,[-\frac{\pi}2,\frac{\pi}2]\,,$ then you don't end up where you started!

Here are the details:

For all $\,x\in [-\frac{\pi}2,\frac{\pi}2]\,,$

(See the top graph above.)

For all $\,x\not\in [-\frac{\pi}2,\frac{\pi}2]\,,$

(See the bottom graph above.)

Example: Find the Exact Value of $\,\arcsin(-0.5)\,$

Use both the unit circle and a special triangle.

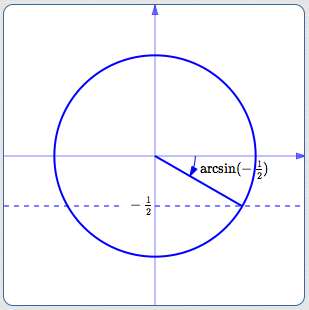
Using the degree definition:  $\,\arcsin (-\frac 12)\,$ is the angle between $\,-90^\circ\,$ and $\,90^\circ\,$ whose sine is $\,-\frac 12\,.$

Recall:  Sine is the $y$-value of points on the unit circle.

Draw a unit circle. Mark $\,-\frac 12\,$ on the $y$-axis. Mark the unique angle between $\,-90^\circ\,$ and $\,90^\circ\,$ that has this sine value. This (negative) angle is $\,\arcsin(-\frac 12)\,.$

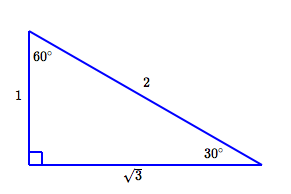
Does any special triangle tell us an acute angle whose sine is $\,\frac12\,$? Yes! The sine of $\,30^\circ\,$ is $\,\frac 12\,.$

Thus, $\,\arcsin(-\frac 12) = -30^\circ\,.$

Using radian measure, $\,\arcsin(-\frac 12) = -\frac{\pi}6\,.$