Trying to ‘Undo’ Trigonometric Functions

Doing and Undoing

You DO things. In math (as in life), only sometimes can you ‘undo’ what you did. Sometimes you can't fully or reliably ‘undo’ something, but you do the best you can.

In math, functions are a common tool to do things. You feed an input into a function. The function does something to the input to produce a unique output.

For example, feed $\,x\,$ into the sine function (‘$\,\sin\,$’, pronounced ‘sine’—long i) and the unique output ‘$\,\sin x\,$’ (sine of $\,x\,$) results, as shown below.

Recall that $\ \sin x\ $ (no parentheses) is a shorthand for $\ \sin(x)\ $ (with parentheses). For multi-letter function names, you can drop the parentheses that hold the input, as long as there is no confusion about order of operations.

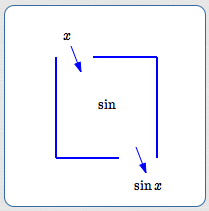
The sine function: input $\,x\,$ gives output $\,\sin x\,$

Going from inputs to outputs is the most common way to use functions. However, sometimes you need to (try and) use functions ‘backwards’.

You want to start with an output and try to get back to an input. Functions do something; you want to try and undo what the function did.

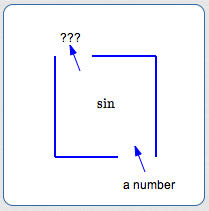
When you try to go from outputs to inputs, you're in the realm of inverse functions.

The questions to be explored in this section are:

• Can the trigonometric functions be ‘undone’?
• Given an output from a trigonometric function (like sine, cosine, or tangent), can we know what input it came from?
• Do the trigonometric functions have (true) inverses?

Trying to use the sine function ‘backwards’

If We Know That $\,\sin x = 0.5\,,$ Can We Know What $\,x\,$ Is?

To illustrate the idea, suppose there's an unknown number $\,x\,.$ All we know about $\,x\,$ is that it's a real number, and when it gets dropped into the sine function, the number $\,0.5\,$ is the corresponding output. Thus, we know that $\,\sin x = 0.5\,.$

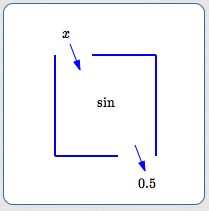
Does this output information uniquely identify the input? That is, does knowing ‘$\,\sin x = 0.5\,$’ uniquely identify $\,x\,$?

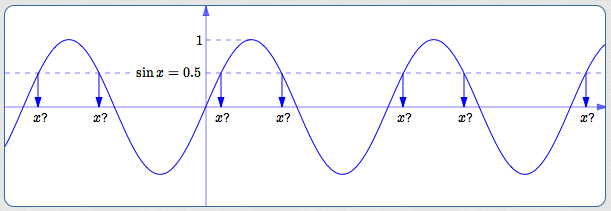
The graph of the sine function (above) shows that the answer is a resounding no!

All the values of $\,x\,$ shown (and infinitely many more, by continuing the pattern to the right and left) satisfy $\,\sin x = 0.5\,.$

Any of these values of $\,x\,$ could have been dropped into the sine function to give the output $\,0.5\,.$ Without additional information, there's no way to know precisely which value of $\,x\,$ produced the output $\,0.5\,.$

The Sine Function Is Not One-To-One, So It Doesn't Have a True Inverse

For the sine function, an output does not uniquely identify an input.

For the sine function, any output (between $\,-1\,$ and $\,1\,$) has infinitely many corresponding inputs. The graph of the sine function does not pass a horizontal line test. The sine function is not one-to-one.

The same problem holds with all the trigonometric functions: sine, cosine, tangent, cotangent, secant, and cosecant. None of them are one-to-one. None of them have true inverses.

This is so important, that it is worth repeating:

Feeling a bit rusty on one-to-one functions and inverse functions? If so, you may want to review the prior sections listed below before continuing:

• Using a Function Box ‘Backwards’
  Some functions can be ‘undone’—others can't. What is the key factor in deciding which are which?
• One-to-One Functions
  Only one-to-one functions can be ‘undone’; only one-to-one functions have inverses. The inverse of a function (when it exists) undoes what the function did.
• Undoing a One-to-One Function; Inverse Functions
  When a function $\,f\,$ is one-to-one, then there exists a unique function $\,f^{-1}\,$ that ‘undoes’ what $\,f\,$ did. The function $\,f^{-1}\,$ is called the inverse of $\,f\,.$
• Properties of Inverse Functions
• The Graph of an Inverse Function

‘Undoing’ Trigonometric Functions—What's The Best We Can Do?

For a function to have an inverse, it must be one-to-one. Trigonometric functions aren't one-to-one, so they don't have true inverses.

However, we still want to be able to go from any output to a corresponding input; it's just that we'll have to choose one particular input from the infinitely-many that are available.

To accomplish this, we'll throw away most of the graph, leaving just a piece that provides us with exactly one input for each of the possible outputs.

More precisely, we need to restrict the domain of the original trigonometric function. We want a ‘restricted version’ that has these three properties:

• Outputs Covered:  The output set for the original trigonometric function and the restricted version must be the same.
• One-To-One:  The restricted version must be one-to-one.
• Close To Origin:  The restricted version should be as close to the origin as possible.

To better understand these three conditions, let's investigate the potential ‘restricted versions of the sine function’ suggested below. For each, answer these questions:

• Does it meet the ‘outputs covered’ condition?
• Does it meet the ‘one-to-one’ condition?
• Does it meet the ‘close to origin’ condition?

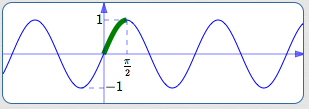
Restrict to the interval $\,[0,\frac{\pi}{2}]$

Outputs covered?	No	(only $\,[0,1]\,$ is covered)
One-to-one?	Yes
Close to origin?	Yes

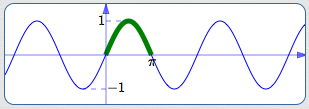
Restrict to the interval $\,[0,\pi]$

Outputs covered?	No	(only $\,[0,1]\,$ is covered)
One-to-one?	No
Close to origin?	Yes

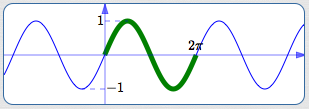
Restrict to the interval $\,[0,2\pi]\,$

Outputs covered?	Yes	(all of $\,[-1,1]\,$)
One-to-one?	No
Close to origin?	Yes

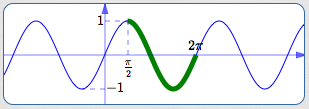
Restrict to the interval $\,[\frac{\pi}{2},2\pi]\,$

Outputs covered?	Yes
One-to-one?	No
Close to origin?	No

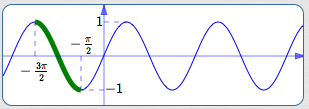
Restrict to the interval $\,[-\frac{3\pi}{2},-\frac{\pi}{2}]$

Outputs covered?	Yes
One-to-one?	Yes
Close to origin?	No

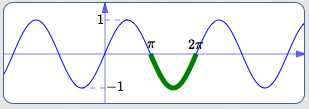
Restrict to the interval $\,[\pi,2\pi]$

Outputs covered?	No	(only $\,[-1,0]\,$ is covered)
One-to-one?	No
Close to origin?	No

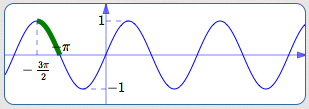
Restrict to the interval $\,[-\frac{3\pi}{2},-\pi]$

Outputs covered?	No	(only $\,[0,1]\,$ is covered)
One-to-one?	Yes
Close to origin?	No

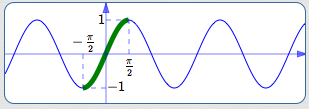
Restrict to the interval $\,[-\frac{\pi}{2},\frac{\pi}{2}]$

Outputs covered?	Yes	(all of $\,[-1,1]\,$)
One-to-one?	Yes
Close to origin?	Yes

The interval $\,[-\frac{\pi}{2},\frac{\pi}{2}]\,$ is the only interval that satisfies all three conditions! Thus, restriction to the interval $\,[-\frac{\pi}{2},\frac{\pi}{2}]\,$ is used to define the inverse sine function.

Given any output (say, $\,0.5\,$) from the sine function, there are infinitely many inputs $\,x\,$ for which $\,\sin x = 0.5\,.$ However, there is only one value of $\,x\,$ between $\,-\frac{\pi}{2}\,$ and $\,\frac{\pi}{2}\,$ that works!

Summary

• The sine function is not one-to-one, hence does not have a true inverse.
• However, given an output (like $\,0.5\,$), we still want a convenient way to produce an input $\,x\,$ for which $\,\sin x = 0.5\,.$
• The problem is that there are infinitely many values of $\,x\,$ for which $\,\sin x = 0.5\,$!
• However, there is only one value of $\,x\,$ between $-\frac{\pi}{2}\,$ and $\,\frac{\pi}{2}\,$ for which $\,\sin x = 0.5\,.$
• Indeed, for any real number $\,y\,$ between $\,-1\,$ and $\,1\,,$ there is only one value of $\,x\,$ between $-\frac{\pi}{2}\,$ and $\,\frac{\pi}{2}\,$ for which $\,\sin x = y\,.$
• The function that the mathematical community calls ‘the inverse sine function’ is actually the inverse of the sine function, restricted to $\,[-\frac{\pi}{2},\frac{\pi}{2}]\,.$ This restriction is one-to-one, hence has a true inverse.
• The inverse sine function is covered precisely in the next section.