Summary: Solving Triangles, All Types (Part 1)

(This page is Part 1. Click here for Part 2.)

To solve a triangle means to find all the angles and all the side lengths.

This section summarizes information related to solving triangles, and presents ‘safe’ solution approaches for all triangle types.

Complete discussions are offered in the sections listed below; consult them as needed.

• Law of Sines
• Given Two Sides and a Non-Included Angle, How Many Triangles?
• Law of Cosines
• Using the Law of Cosines in the SSS Case (& Introduction to the Arccosine Function)

Notation

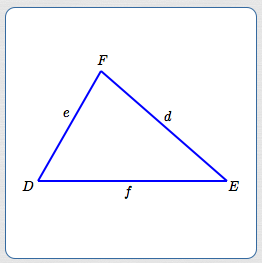
Capital letters are used to denote angles/vertices. Corresponding lowercase letters are used to denote lengths of opposite sides. Thus:

• angle $\,D\,$ is opposite side $\,d$
• angle $\,E\,$ is opposite side $\,e$
• angle $\,F\,$ is opposite side $\,f$

Easy-To-Use Triangle Solver

If you just need to solve a triangle reliably, here's an easy-to-use triangle solver. It can also be used to check your work.

Basic Tools/Ideas Useful for Solving Triangles

In Any Triangle:

• the angles sum to $\,180^\circ\,$
• angles are strictly between $\,0^\circ\,$ and $\,180^\circ$
• there is at most one angle that is $\,\ge 90^\circ$

• If a triangle has longest/medium/shortest sides, then:

  • the longest side is opposite the biggest angle
  • the medium side is opposite the medium angle
  • the shortest side is opposite the smallest angle
• sides opposite equal angles are equal
• angles opposite equal sides are equal

Law of Sines

• Law of Sines: In any triangle, the ratio of the sine of an angle to the length of its opposite side is constant:

  $$\cssId{s32}{\frac{\sin D}{d} = \frac{\sin E}{e} = \frac{\sin F}{f}}$$
• To use the Law of Sines, you must know an angle and its opposite side.
• If an unknown angle is ‘inside’ a sine, then you will ‘undo’ the sine with the arcsine function (abbreviated ‘$\,\arcsin\,$’).

• By definition, for $\,-1 \le x\le 1\,$:   $\,\arcsin(x) := $ the angle between $\,-90^\circ\,$ and $\,90^\circ\,$ whose sine is $\,x\,.$

• In the context of solving triangles, $\,\arcsin(x)\,$ is always an angle in the interval $\,(0^\circ,90^\circ]\,.$

• If a calculator is in degree mode, then $\,\arcsin(x)\,$ is reported in degrees.

  If a calculator is in radian mode, then $\,\arcsin(x)\,$ is reported in radians.

• If $\,D \le 90^\circ\,,$ then $\,D = \arcsin(\sin D)\,.$

  If $\,D\,$ is obtuse, then $\,D = 180^\circ - \arcsin(\sin D)\,.$

• Caution: If $\,D\,$ is an unknown angle in a triangle and you know $\,\sin D\,,$ then $\,\arcsin(\sin D)\,$ may not give you the angle you want!

• Good Habit: To avoid problems associated with the Law of Sines and the arcsine, always use the Law of Sines with the shortest side available.

  Memory device:  Law of Sines/Shorter

Law of Cosines

• Law of Cosines: In any triangle, the square of a side is the sum of the squares of the other two sides, minus twice the product of the other two sides times the cosine of the included angle:

  $$\cssId{s53}{d^2 = e^2 + f^2 - 2ef\cos D}$$

  (There are two other versions.)

• To use the Law of Cosines, you must know at least two sides.

  Know two sides and the included angle? Solve for the remaining side.

  Know three sides? Solve for an angle. (Good habit: solve for the biggest angle.)

• If an unknown angle is ‘inside’ a cosine, then you will ‘undo’ the cosine with the arccosine function (abbreviated ‘$\,\arccos\,$’).

• By definition, for $\,-1 \le x\le 1\,$:   $\arccos(x) :=$ the angle between $\,0^\circ\,$ and $\,180^\circ\,$ whose cosine is $\,x\,.$

• If a calculator is in degree mode, then $\,\arccos(x)\,$ is reported in degrees.

  If a calculator is in radian mode, then $\,\arccos(x)\,$ is reported in radians.

• For all angles in triangles, $\,D = \arccos(\cos D)\,.$
• If $\,D\,$ is an unknown angle in a triangle and you know $\,\cos D\,,$ then $\,\arccos(\cos D)\,$ is always the angle you want!
• The Law of Cosines is ‘safer’ to use than the Law of Sines when solving triangles.

• Good Habit: Use the Law of Cosines with the biggest angle available (i.e., the angle opposite a longest side).

  If a triangle has an obtuse angle, then the Law of Cosines will find it correctly, leaving only acute angles to be used with the Law of Sines.

  This can help prevent ‘impossible’ triangles caused by an ‘uninformed’ use of the Law of Sines. See What Can Go Wrong? in Part 2.

Special Tools for Right Triangles

• The Pythagorean Theorem:  In a right triangle, the square of the hypotenuse is the sum of the squares of the other two sides:

  $$\cssId{s75}{d^2 = e^2 + f^2}$$

  Here, $\,d\,$ is the hypotenuse (the side opposite the right angle).

  It works the other direction, too: if a triangle satisfies $\,d^2 = e^2 + f^2\,,$ then it's a right triangle.

• Right Triangle Definitions (SOHCAHTOA):

  $$\begin{gather} \cssId{s80}{\sin\theta = \frac{\text{OPP}}{\text{HYP}}}\cr\cr \cssId{s81}{\cos\theta = \frac{\text{ADJ}}{\text{HYP}}}\cr\cr \cssId{s82}{\tan\theta = \frac{\text{OPP}}{\text{ADJ}}} \end{gather} $$

• There's a function that ‘undoes’ the tangent, similar to how the $\,\text{arcsin}\,$ ‘undoes’ the sine, and the $\,\text{arccos}\,$ ‘undoes’ the cosine.

  By definition, for all real numbers $\,x\,$:   $\arctan(x) :=\,$ the angle strictly between $\,-90^\circ\,$ and $\,90^\circ\,$ whose tangent is $\,x\,.$

  In the context of solving triangles, $\,\arctan(x)\,$ is always an angle in the interval $\,(0^\circ,90^\circ)\,.$

  Arctan is ‘safe’ to use if you know the angle you're working with is acute.

Computational Considerations

Good Habit:  When solving triangles, select tools that use exact values, whenever possible.

For example, suppose you're solving the right triangle shown below.

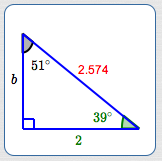
Green numbers are given (exact) values ($\,\color{green}{2}\,$ and $\,\color{green}{39^\circ}\,$).

Black numbers are computed exact values ($\,51^\circ\,$).

Red numbers are computed approximate values ( $\,\color{red}{2.574}\,$).

To compute $\,b\,,$ you should use

since they use only exact values.

since they use computed approximate values, which introduce more computational error.

Good Habit:  Use the full accuracy of your calculator, whenever possible. For example, if you've computed $\,2.574...\,$ and must use it later on, then use your calculator features (e.g., memory, recent values) to use all the calculator digits. Don't just type in the four digits $\,2.574\,$!

Special Triangles

Be on the lookout for these special triangles. When you recognize them, you should be able to fill in values from memory (no computations).

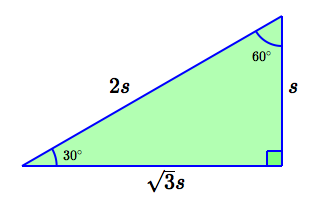
$30^\circ\,$-$\,60^\circ\,$-$\,90^\circ\,$ triangle

Shortest side:	opposite $\,30^\circ\,$ angle
Hypotenuse:	twice the shortest side
Medium side:	$\,\sqrt{3}\,$ times the shortest side

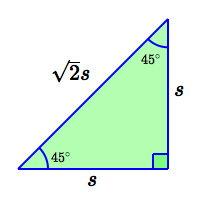
$45^\circ\,$-$\,45^\circ\,$-$\,90^\circ\,$ triangle

Hypotenuse is $\,\sqrt{2}\,$ times the length of the leg