Given Two Sides and a Non-Included Angle, How Many Triangles? (Part 1)

(This page is Part 1. Click here for Part 2.)

The ‘SSA’ triangle condition (two sides and a non-included angle), does not uniquely identify a triangle.

Given two positive real numbers (two side lengths) and a degree measure strictly between $\,0^\circ\,$ and $\,180^\circ\,$ (the angle), there may be no triangle, exactly one triangle, or two triangles that match the SSA information.

The information in Is there an ‘SSA’ congruence theorem? No! is re-visited, adding details to determine precisely when you have zero, one, or two triangles.
The arcsine function is quickly introduced (in Part 2), since it is needed to solve an SSA situation.
Examples are given (in Part 2), using the Law of Sines to investigate SSA situations.

When Will You Have Zero, One, or Two Triangles in an ‘SSA’ Situation?

Let $\,a\,$ and $\,b\,$ be positive real numbers, used to denote lengths of two sides of a triangle. Let $\,\theta\,$ denote the measure of a non-included angle.

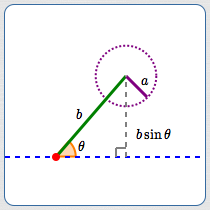
illustrating the SSA condition for triangles

As shown above, $\,a\,,$ $\,b\,$ and $\,\theta\,$ form an ‘SSA’ situation—two sides and a non-included angle.

To significantly cut down on words, I say things like:

‘$\,a\,$ attaches to $\,b\,$’

instead of the more correct (but much wordier):

‘The side of length $\,a\,$ attaches to the side of length $\,b\,$’

Note that:

‘SSA’ corresponds to ‘$\,a\,b\,\theta\,$’
$b\,$ attaches to $\,a\,$ at one end and has $\,\theta\,$ at the other end
$a\,$ is opposite $\,\theta$

To sketch an SSA situation for given values of $\,a\,,$ $\,b\,$ and $\,\theta\,$:

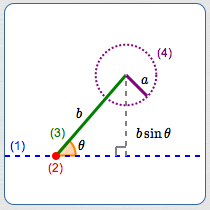
Start by drawing a dashed line that will ‘hold’ the third (unknown) side of the triangle.
Choose a point on the dashed line as the vertex for $\,\theta\,.$
Attach the side of length $\,\color{green}{b}\,$ to the chosen vertex at angle $\,\color{orange}{\theta}\,.$
At the other end of $\,b\,,$ attach a circle of radius $\,\color{purple}{a}\,$; the angle at which $\,b\,$ attaches to $\,a\,$ is initially unknown.

The altitude shown (which has length $\,b\sin\theta\,$) is an important boundary between different behaviors—keep reading!

In the following progression of sketches, $\,b\,$ and $\,\theta\,$ are held constant, and $\,\theta\,$ is an acute angle. The side of length $\,a\,$ gets bigger and bigger:

$0 \lt a \lt b\sin\theta$

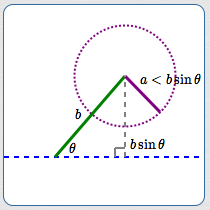
NO triangle determined by an SSA condition

When $\,a\,$ is less than $\,b\sin\theta\,,$ it is too short to reach the dashed line. No matter what the angle is between $\,a\,$ and $\,b\,,$ the triangle cannot be completed.

For $\,0 \lt a \lt b\sin\theta\,,$ there is no triangle determined by sides $\,a\,$ and $\,b\,$ and a non-included angle $\,\theta\,.$

$0 \lt a \lt b\sin\theta$
No triangle determined by $\,a\,,$ $\,b\,$ and $\,\theta\,$

$a = b\sin\theta$

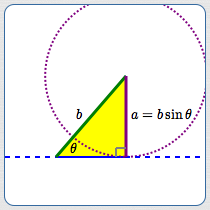
EXACTLY ONE triangle determined by an SSA condition

When $\,a\,$ reaches the altitude length ($\,a = b\sin\theta\,$) then it is just long enough to hit the dashed line and form a (right) triangle.

For $\,a = b\sin\theta\,,$ there is exactly one (right) triangle determined by sides $\,a\,$ and $\,b\,$ and a non-included angle $\,\theta\,.$

$a = b\sin\theta$
Exactly one (right) triangle determined by $\,a\,,$ $\,b\,$ and $\,\theta$

$b\sin\theta \lt a \lt b$

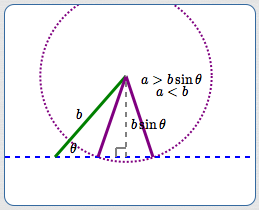
TWO triangles determined by an SSA condition

This is the most interesting case! This case is the reason there is no ‘SSA’ congruence theorem.

For values of $\,a\,$ strictly between $\,b\sin\theta\,$ and $\,b\,,$ the circle of radius $\,a\,$ intersects the dashed line at two different points.

Therefore, there are two different triangles that meet the SSA information.

For $\,b\sin\theta \lt a \lt b\,,$ there are two different triangles determined by sides $\,a\,$ and $\,b\,$ and a non-included angle $\,\theta\,.$

The two triangles determined by $\,a\,,$ $\,b\,$ and $\,\theta\,$:

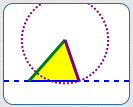
one of the two triangles determined in an SSA situation

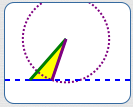
another of the two triangles determined in an SSA situation

$\,b\sin\theta \lt a \lt b\,$
Two different triangles determined by $\,a\,,$ $\,b\,$ and $\,\theta\,$

$a = b$

For $\,a = b\,,$ there is exactly one isosceles triangle determined by sides $\,a\,$ and $\,b\,$ and a non-included angle $\,\theta\,.$

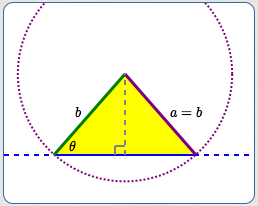
exactly one triangle in an SSA situation

$a = b$
Exactly one isosceles triangle

$a \gt b$

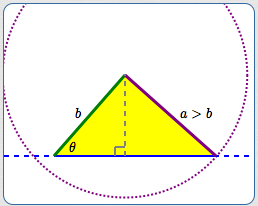
exactly one triangle determined in an SSA situation

When $\,a\,$ is greater than $\,b\,,$ then the circle of radius $\,a\,$ intersects the dashed line at two different points. However, only one of these points gives a triangle with interior angle $\,\theta\,.$

For $\,a \gt b\,,$ there is exactly one triangle determined by sides $\,a\,$ and $\,b\,$ and a non-included angle $\,\theta\,.$

$a \gt b$
Exactly one triangle

Summary: Boundaries for Zero, One, Two Triangles in an SSA Configuration

This graphic summarizes the ‘SSA’ situations discussed above.

Side $\,b\,$ and angle $\,\theta \lt 90^\circ\,$ are fixed. The number line shows the values of $\,a\,$ corresponding to no, one, and two triangles.

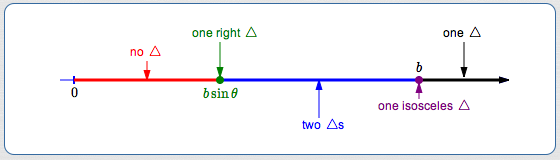
Summary: Boundaries for zero, one, two triangles in an SSA configuration

The red (no $\,\triangle\,$), blue (two $\,\triangle\,$s), and black (one $\,\triangle\,$) intervals change depending upon the values of $\,b\,$ and $\,\theta\,.$

Put in your own values for $\,b\,$ and $\,\theta\,$ below—have fun!

Play With SSA Configurations

Type in desired values for $\,b\,$ and $\,\theta\,$ below. Then, click the ‘Create Number Line Summary’ and ‘See the Triangle’ buttons.

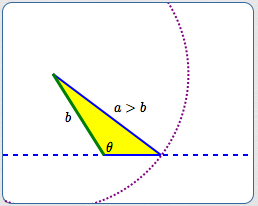
Note: If $\,\theta\,$ is an obtuse angle (or a right angle), then the situation is different. In this case, no triangle exists until $\,a \gt b\,,$ at which point there is a unique triangle:

what SSA looks like with an obtuse angle

Practice Sketching SSA Cases

Get a random SSA situation by clicking below. Sketch the given situation on a piece of paper—make it roughly to scale, but don't actually measure anything. Based on your sketch, make a conjecture as to how many triangle(s) meet this SSA configuration. Then, check your conjecture.