 Summary: Solving Triangles, All Types (Part 2)
Summary: Solving Triangles, All Types (Part 2)
(This page is Part 2. Click here for Part 1.)
Solving Triangles: What Can Go Wrong?
The following example illustrates what can go wrong when solving triangles, if good habits are not followed.
Example
Consider a triangle with sides of length $\,3\,,$ $\,4\,$ and $\,6\,.$ Solve the triangle.
Faulty Solution
Let $\,D,\, E,\, F\,$ be the angles across from the sides of length $\,3,\, 4,\, 6\,.$ Note that $\,6 \lt 3 + 4\,.$ By SSS, the triangle is unique.
By the Law of Cosines:
$$ \begin{gather} \cssId{s8}{ 3^2 = 4^2 + 6^2 - 2\cdot 4\cdot 6\cdot\cos D}\cr\cr \cssId{s9}{\cos D \approx 0.8958} \cr\cr \cssId{s10}{ D = \arccos(\cos D) \approx 26.38^\circ} \end{gather} $$By the Law of Sines:
$$ \begin{gather} \cssId{s12}{\frac{\sin 26.38^\circ}{3} = \frac{\sin F}{6}}\cr\cr \cssId{s13}{\sin F = \frac{6\sin 26.38^\circ}{3} \approx 0.8886}\cr\cr \cssId{s14}{F = \arcsin(0.8886) \approx 62.70^\circ}\cr \color{red}{\text{(The mistake is here!)}}\cr\cr \end{gather} $$Summary:
| Angles | Opposite Sides |
| $D = 26.38^\circ$ | $d = 3$ |
| $E = 90.92^\circ$ | $e = 4$ |
| $F = 62.70^\circ$ | $f = 6$ |
This is an ‘impossible triangle’!
- The longest side is not opposite the biggest angle.
- The Law of Sines ratios are not all equal: $$ \begin{gather} \cssId{s28}{\frac{\sin 26.38^\circ}{3} \approx 0.1481} \cr\cr \cssId{s29}{\frac{\sin 90.92^\circ}{4} \approx 0.2500} \end{gather} $$
An application of just one of the two recommended ‘good habits’ would have prevented the impossible triangle. Here, both good habits are applied:
Correct Solution
Let $\,D,\, E,\, F\,$ be the angles across from the sides of length $\,3,\, 4,\, 6\,.$ Note that $\,6 \lt 3 + 4\,.$ By SSS, the triangle is unique.
Use the Law of Cosines with the longest side:
$$ \begin{gather} \cssId{s36}{6^2 = 3^2 + 4^2 - 2\cdot 3\cdot 4\cdot\cos F}\cr\cr \cssId{s37}{\cos F \approx -0.4583} \cr\cr \cssId{s38}{F = \arccos(\cos F) \approx 117.3^\circ} \end{gather} $$Use the Law of Sines with the shortest side:
$$ \begin{gather} \cssId{s40}{\frac{\sin 117.3^\circ}{6} = \frac{\sin D}{3}}\cr\cr \cssId{s41}{\sin D = \frac{3\sin 117.3^\circ}{6} \approx 0.4443}\cr\cr \cssId{s42}{D = \arcsin(0.4443) \approx 26.38^\circ} \end{gather} $$Summary:
| Angles | Opposite Sides |
| $D = 26.38^\circ$ | $d = 3$ |
| $E = 36.32^\circ$ | $e = 4$ |
| $F = 117.3^\circ$ | $f = 6$ |
This is the correct triangle!
Corrections From the Faulty Solution
Note: The corrections would be:
Congruence Theorems
Congruence Theorems
A unique triangle is determined by each of these configurations:
SAS
Side-Angle-Side
(Two Sides and an Included Angle)
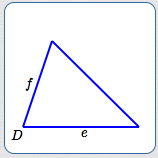
If
$$\begin{gather} \cssId{s65}{e \gt 0}\cr \cssId{s66}{f \gt 0}\cr \cssId{s67}{0^\circ \lt D \lt 180^\circ} \end{gather} $$then there exists a unique triangle having the two sides and included angle.
SSS
Side-Side-Side
(Three Sides)
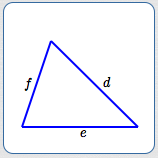
Name the sides so that:
$$\cssId{s73}{0 \lt f \le e \le d}$$Then, if
$$\cssId{s75}{d \lt e + f}$$the triangle exists and is unique.
That is: the longest side (if there is one) must be strictly less than the sum of the two other sides.
AAS/SAA
Angle-Angle-Side
(or, Side-Angle-Angle)
(Two Angles and a Non-Included Side)
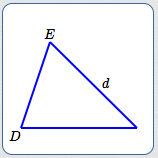
If
$$ \begin{gather} \cssId{s84}{0^\circ \lt D \lt 180^\circ}\cr \cssId{s85}{0^\circ \lt E \lt 180^\circ}\cr \cssId{s86}{D + E \lt 180^\circ}\cr \cssId{s87}{d \gt 0} \end{gather} $$then there exists a unique triangle having the two angles and non-included side.
Note: Two angles uniquely determine the third, and uniquely define the shape. One side uniquely defines the size.
ASA
Angle-Side-Angle
(Two Angles and an Included Side)
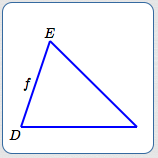
If
$$ \begin{gather} \cssId{s97}{0^\circ \lt D \lt 180^\circ}\cr \cssId{s98}{0^\circ \lt E \lt 180^\circ}\cr \cssId{s99}{D + E \lt 180^\circ}\cr \cssId{s100}{f \gt 0} \end{gather} $$then there exists a unique triangle having the two angles and included side.
Note: Two angles uniquely determine the third, and uniquely define the shape. One side uniquely defines the size.
‘Safe’ Approaches for Solving Triangles
‘Safe’ Triangle-Solving Strategies
By using the guidelines here, you will avoid a mistake leading to an ‘impossible’ triangle.
When it is safe to do so, the Law of Sines is preferred over the Law of Cosines, since it requires fewer computations.
Once two angles are known, find the third angle using the fact that the angles sum to $\,180^\circ\,.$
SAS

Step 1: Use the Law of Cosines to find $\,d\,.$
Step 2: Use the Law of Sines with the shorter of $\,e\,$ or $\,f\,.$
Why? A triangle can have at most one obtuse angle. Therefore, at most one of $\,E\,$ or $\,F\,$ is obtuse. Whichever is opposite the shorter side is guaranteed to be acute.
For acute angles:
$$\cssId{s119}{D = \arcsin(\sin D)}$$SSS

Step 1: Let $\,d\,$ denote the longest side (if there is one).
Step 2: Use the Law of Cosines to find $\,D\,.$ If there is an obtuse angle, the Law of Cosines will find it correctly, and the remaining two angles will be acute.
Step 3: Use the Law of Sines to find a second angle.
AAS/SAA

Step 1: Use the angle sum property to find the third angle.
Step 2: Use the Law of Sines twice to find the remaining two sides.
Note: There is no danger in using the Law of Sines when the unknown is a side.
ASA

Step 1: Use the angle sum property to find the third angle.
Step 2: Use the Law of Sines twice to find the remaining two sides.
Note: There is no danger in using the Law of Sines when the unknown is a side.
Other Triangle Configurations
AAA (Angle Angle Angle)
Infinitely many triangles have the same three angles. Therefore, you cannot ‘solve’ an AAA triangle.
Triangles with the same angles are called similar triangles.
Similar triangles have the same shape, but not necessarily the same size.
Specifying the length of just one side determines the size. This is the justification for the AAS and ASA congruence theorems.
SSA/ASS (Side Side Angle, Angle Side Side)
The ‘SSA’ triangle condition (two sides and a non-included angle), does not uniquely identify a triangle.
Given two positive real numbers (two side lengths) and a degree measure strictly between $\,0^\circ\,$ and $\,180^\circ\,$ (the angle), there may be no triangle, exactly one triangle, or two triangles that match the SSA information.
The cut-off points for different behaviors are summarized below. See Given Two Sides and a Non-Included Angle, How Many Triangles? for details.
You don't need to (and shouldn't) memorize the table below! The mathematics will tell you which situation you're in (zero, one, or two triangles), providing you do the mathematics correctly!
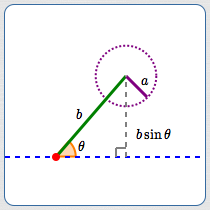
Let:
$$\begin{gather} \cssId{s155}{a \gt 0}\cr \cssId{s156}{b \gt 0}\cr \cssId{s157}{0^\circ \lt \theta \lt 180^\circ} \end{gather} $$Note: the side of length $\,a\,$ is opposite the known angle $\,\theta\,.$
$\theta \lt 90^\circ$
|
|
| $0 \lt a \lt b\sin\theta$ | no triangle |
| $a = b\sin\theta$ | exactly one right triangle |
| $b\sin\theta \lt a \lt b$ | two different triangles |
| $a = b$ | exactly one isosceles triangle |
| $a > b$ | exactly one triangle |
$\theta \ge 90^\circ$
|
|
| $0 \lt a \le b$ | no triangle |
| $a \gt b$ | exactly one triangle |
Solving SSA Configurations: Two Approaches
Each approach is illustrated with this example: Suppose a triangle has a $\,50^\circ\,$ angle opposite a side of length $\,6\,.$ A second side has length $\,7\,.$ Solve the triangle.
Start by defining notation: Let $\,E\,$ be the angle opposite the side of length $\,7\,.$ Let $\,F,\,f\,$ be the remaining unknown angle and opposite side.
First Approach: Use the Law of Sines—Just Be Careful
Recognize the SSA configuration. Be aware of the potential for zero, one, or two triangles.
Use the Law of Sines to get both potential angles:
$$ \cssId{s190}{\frac{\sin 50^\circ}{6} = \frac{\sin E}{7}} $$Get both potential third angles:
(Of course, discard a situation that results in a nonpositive angle.)
Use the Law of Sines to find the remaining side(s):
$$ \begin{gather} \cssId{s199}{\frac{\sin 50^\circ}{6} = \frac{\sin 66.66^\circ}{f_1}}\cr \cssId{s200}{\text{so}}\cr \cssId{s201}{f_1 \approx 7.19}\cr\cr\cr \cssId{s202}{\frac{\sin 50^\circ}{6} = \frac{\sin 13.34^\circ}{f_2}}\cr \cssId{s203}{\text{so}}\cr \cssId{s204}{f_2 \approx 1.81} \end{gather} $$Compare the results of both approaches. Different approaches may yield slightly different results. Greater accuracy at intermediate steps will help to minimize differences.
Second Approach: Use the Law of Cosines—Solve a Quadratic Equation
Recognize the SSA configuration. Be aware of the potential for zero, one, or two triangles.
Use the Law of Cosines starting with the side across from the known angle:
$$ \cssId{s212}{6^2 = 7^2 + f^2 - 2\cdot 7\cdot f\cos 50^\circ} $$Solve the quadratic equation. It may give zero, one, or two solutions for $\,f\,$:
$$ \begin{gather} \cssId{s215}{f^2 - (14\cos 50^\circ)f + 13 = 0}\cr\cr \cssId{s216}{f = \frac{14\cos 50^\circ \pm \sqrt{14^2\cos^2 50^\circ - 4(13)}}{2}}\cr\cr \cssId{s217}{f_1 \approx 7.19}\cr \cssId{s218}{f_2 \approx 1.81} \end{gather} $$Use the Law of Sines on each configuration. Choose the shortest available side for each configuration.
Note:
First configuration: $\,e_1 = 7\,$ and $\,f_1 = 7.19\,,$ so $\,\color{red}{7} \lt 7.19$
Second configuration: $\,e_2 = 7\,$ and $\,f_2 = 1.81\,,$ so $\,\color{green}{1.81} \lt 7$
$$ \begin{gather} \cssId{s226}{\frac{\sin 50^\circ}{6} = \frac{\sin E_1}{\color{red}{7}}}\cr \cssId{s227}{\text{so}}\cr \cssId{s228}{E_1 \approx 63.34^\circ}\cr\cr\cr \cssId{s229}{\frac{\sin 50^\circ}{6} = \frac{\sin F_2}{\color{green}{1.81}}}\cr \cssId{s230}{\text{so}}\cr \cssId{s231}{F_2 \approx 13.36^\circ} \end{gather} $$Compute the remaining angles: