The Pythagorean Theorem

A $\,90^\circ$ angle is called a right angle. A right triangle is a triangle with a $\,90^\circ\,$ angle.

In a right triangle, the side opposite the $\,90^\circ$ angle is called the hypotenuse and the remaining two sides are called the legs.

The angles in any triangle add up to $\,180^\circ\,.$

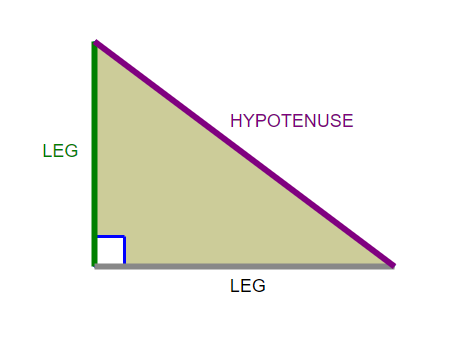
In any triangle, the longest side is opposite the largest angle, and the shortest side is opposite the smallest angle. Thus, in a right triangle, the hypotenuse is always the longest side.

The Pythagorean Theorem gives a beautiful relationship between the lengths of the sides in a right triangle: the sum of the squares of the shorter sides is equal to the square of the hypotenuse. Furthermore, if a triangle has this kind of relationship between the lengths of its sides, then it must be a right triangle!

THEOREM The Pythagorean Theorem

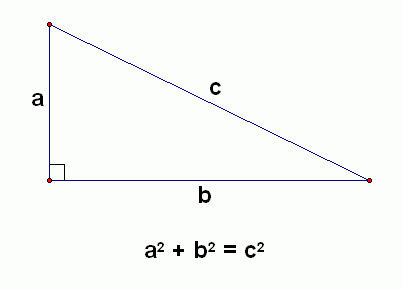
Let $\,\,T\,\,$ be a triangle with sides of lengths $\,a\,,$ $\,b\,,$ and $\,c\,,$ where $\,c\,$ is the longest side (if there is a longest side). Then: $$ \begin{gather} \cssId{s15}{\text{$T\,$ is a right triangle}}\cr\cr \cssId{s16}{\text{if and only if}}\cr\cr \cssId{s17}{a^2 + b^2 = c^2} \end{gather} $$

Have fun with many proofs of the Pythagorean Theorem! This applet (you'll need Java) is one of my favorites. Let it load, then keep pressing ‘Next’.

Examples

Question: Suppose that two angles in a triangle are $\,60^\circ$ and $\,30^\circ.$ Is it a right triangle? Answer YES, NO, or MAYBE.

Solution: Yes. The third angle must be $\,180^\circ - 60^\circ - 30^\circ = 90^\circ\,.$

Question: Suppose that a triangle has a $\,100^\circ$ angle. Is it a right triangle? Answer YES, NO, or MAYBE.

Solution: No. The remaining two angles must sum to $\,80^\circ,$ so neither remaining angle is a $\,90^\circ$ angle.

Question: Suppose that a triangle has a $\,70^\circ$ angle. Is it a right triangle? Answer YES, NO, or MAYBE.

Solution: Maybe. The remaining two angles must sum to $\,110^\circ,$ so one of the remaining angles could be a $\,90^\circ$ angle.

Question: Suppose the legs of a right triangle have lengths $\,3\,$ and $\,x\,,$ and the hypotenuse has length $\,5\,.$ Find $\,x\,.$

Solution: $$ \begin{gather} \cssId{s48}{3^2 + x^2 = 5^2}\cr \cssId{s49}{9 + x^2 = 25}\cr \cssId{s50}{x^2 = 16}\cr \cssId{s51}{x = 4} \end{gather} $$

Note: $x\,$ cannot equal $\,-4\,,$ because lengths are always positive.

The $\,3{-}4{-}5\,$ triangle is a well-known right triangle. Multiplying all the sides of a triangle by the same positive number does not change the angles. Thus, if you multiply the sides of a $\,3{-}4{-}5\,$ triangle by any positive real number $\,k\,,$ then you will still have a right triangle. For example, these are all right triangles:

$6{-}8{-}10$	($\,k = 2\,$)
$9{-}12{-}15$	($\,k = 3\,$)
$1.5{-}2{-}2.5$	( $\,k = 0.5\,$ )
$3\pi{-}4\pi{-}5\pi$	($\,k = \pi\,$ )
and so on!

Question: Suppose a triangle has sides of lengths $\,1\,,$ $\,\sqrt{3}\,,$ and $\,2\,.$ Is it a right triangle?

Solution: Yes. Since $\,2 \gt \sqrt{3}\,,$ the longest side has length $\,2\,.$ And: $$ \cssId{s76}{1^2 + {(\sqrt{3})}^2} \cssId{s77}{= 1 + 3} \cssId{s78}{= 4} \cssId{s79}{= 2^2} $$

The Pythagorean Theorem

Examples

Concept Practice