TWO SPECIAL TRIANGLES

• PRACTICE (online exercises and printable worksheets)

You should know the relationship between the lengths of the sides in two special triangles:

• $\,30^\circ{-}60^\circ{-}90^\circ\,$ triangles
• $\,45^\circ{-}45^\circ{-}90^\circ\,$ triangles

$\,30^\circ\text{-}60^\circ\text{-}90^\circ\,$ TRIANGLE

Lengths of Sides in a $\,30^\circ\text{-}60^\circ\text{-}90^\circ\,$ Triangle Let $\,s\,$ denote the length of the shortest side. Then, the hypotenuse has length $\,2s\,$. The side opposite the $\,60^\circ\,$ angle has length $\,\sqrt{3}s\,$. Conversely, if a triangle has sides of lengths $\,s\,$, $\,\sqrt{3}s\,$, and $\,2s\,$, then it is a $\,30^\circ\text{-}60^\circ\text{-}90^\circ\,$ triangle. Since $\,\sqrt{3}\approx 1.7\,$, it follows that the side opposite the $\,60^\circ\,$ angle is a little more than one and a half times the shortest side.

$\,45^\circ\text{-}45^\circ\text{-}90^\circ\,$ TRIANGLE

Lengths of Sides in a $\,45^\circ\text{-}45^\circ\text{-}90^\circ\,$ Triangle Let $\,s\,$ denote the length of the two shorter sides. Then, the hypotenuse has length $\,\sqrt{2}s\,$. Conversely, if a triangle has sides of lengths $\,s\,$, $\,s\,$, and $\,\sqrt{2}s\,$, then it is a $\,45^\circ\text{-}45^\circ\text{-}90^\circ\,$ triangle. Since $\,\sqrt{2}\approx 1.4\,$, it follows that the hypotenuse is a little less than one and a half times the shortest side.

It's easy to see that these are the correct relationships between the lengths of the sides, as follows:

Start with an equiangular (hence equilateral) triangle, where each side has length $\,2\,$.
Notice that all the angles must be $\,\frac{180^\circ}{3} = 60^\circ\,$.
Drop a perpendicular, as shown below.
The purple and green triangles are $\,30^\circ\text{-}60^\circ\text{-}90^\circ\,$ triangles, where the length of the shortest side is $\,1\,$.
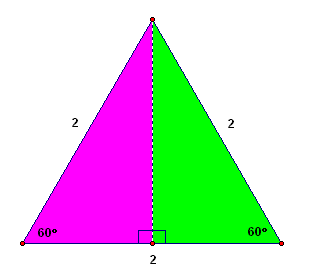
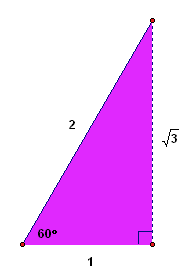
A quick application of the Pythagorean Theorem shows that the remaining side has length $\,\sqrt{3}\,$.
Then, scale all sides by $\,s\,$.

Create a triangle with two sides of length $\,1\,$ and a $\,90^\circ\,$ angle, as shown below.
Since angles opposite equal sides must be equal,
and since the two remaining angles must add to $\,90^\circ\,$,
they must each be $\,45^\circ\,$.
A quick application of the Pythagorean Theorem shows that the remaining side must equal $\,\sqrt{2}\,$.
Then, scale all sides by $\,s\,$.

On this exercise, you will not key in your answer. However, you can check to see if your answer is correct.

PROBLEM TYPES: 1 2 3 4 5 6 7 8 9 10 11 12 13 AVAILABLE MASTERED IN PROGRESS