Similarity, Ratios, and Proportions

Here's a real-life ratio problem that was prompted by a Facebook post: Hummingbirds versus Bees

Suppose you have a triangle that you'd like to enlarge. That is, you want to keep the shape exactly the same, but you want it to be bigger.

Perhaps you want an enlarged copy where the length of each side is three times the size of the original, as shown below:

Or, perhaps you have a quadrilateral that you'd like to reduce. That is, you want to keep the shape exactly the same, but you want it to be smaller.

Perhaps you want a reduced copy where the length of each side is half the size of the original, as shown below:

In both cases, you are keeping the angles exactly the same, and you are multiplying all the sides by an appropriate scaling factor. When you made it three times as big, the scaling factor was $\,3\,.$ When you made it half as big, the scaling factor was $\,0.5\,.$

This idea of keeping the shape the same, but changing the size is made precise by the concept of similarity. Very roughly, two geometric figures are said to be similar when they have the same shape, but not necessarily the same size.

To make the concept of similarity precise, we first need to review ratios and proportions.

DEFINITION ratio

Let $\,a\,$ and $\,b\,$ be real numbers, with $\,b\neq 0\,.$

The ‘ratio of $\,a\,$ to $\,b\,$’ is the quotient $\displaystyle\,\frac{a}{b}\,.$

A ratio automatically brings a scaling factor into the picture, as follows.

Start by giving the ‘ratio of $\,a\,$ to $\,b\,$’ a simpler name, $\,s\,.$ (We're calling it $\,s\,$ because it will be our scaling factor.)

$$\cssId{s22}{s := \frac{a}{b}}$$

(The notation ‘$\,:=\,$’ is frequently used in mathematics to mean equals, by definition.)

Solving for $\,a\,$ gives $\,a=sb\,.$ So, $\,b\,$ has been scaled by $\,s\,$ to give $\,a\,.$

If $\,s=3\,,$ then $\,a=3b\,,$ so that $\,a\,$ is three times bigger than $\,b\,.$ If $\,s=0.5\,,$ then $\,a=0.5b\,,$ so that $\,a\,$ is half as big as $\,b\,.$

When we scale geometric figures, equal ratios automatically enter the picture.

Consider the picture below, where a quadrilateral has been scaled by a factor of $\,s\,$ (here, $\,s\,$ is greater than one) to get a new quadrilateral:

Notice that $\,A=sa\,$ and $\,B=sb\,$ and $\,C=sc\,$ and $\,D=sd\,.$

Solving for $\,s\,$ in each of these four equations gives an equality of four ratios:

$$ \cssId{s38}{s = \frac{A}{a}} \cssId{s39}{= \frac{B}{b}} \cssId{s40}{= \frac{C}{c}} \cssId{s41}{= \frac{D}{d}} $$

Thus, equality of ratios arises very naturally in any scaling situation. An equality of ratios is called a proportion:

DEFINITION proportion

A proportion is an equality of ratios.

Therefore, a proportion takes the form:

$$ \cssId{s48}{\frac{A}{a} = \frac{B}{b}} $$

Using just a little bit of algebra, many useful equalities arise from proportions:

THEOREM equivalent proportions

Let $\,a\,,$ $\,b\,,$ $\,A\,,$ and $\,B\,$ be nonzero real numbers.

Then, the following are equivalent:

$\displaystyle\frac{A}{a} = \frac{B}{b}$
$\displaystyle\frac{a}{A} = \frac{b}{B}$
$\displaystyle\frac{a}{b} = \frac{A}{B}$
$\displaystyle\frac{b}{a} = \frac{B}{A}$

Think about these proportions in the context of a scaled quadrilateral:

Some of the proportions, like $$ \cssId{s60}{\frac{A}{a} = \frac{B}{b}}\ \ \cssId{s61}{\text{ and }}\ \ \cssId{s62}{\frac{a}{A} = \frac{b}{B}} $$ compare ratios between the two quadrilaterals.

Some of the proportions, like $$ \cssId{s65}{\frac{a}{b} = \frac{A}{B}}\ \ \cssId{s66}{\text{ and }}\ \ \cssId{s67}{\frac{b}{a} = \frac{B}{A}} $$ compare ratios within the two quadrilaterals.

In both cases, attaching words to the proportions may be useful. For example, you can read

$$\cssId{s71}{\frac{A}{a} = \frac{B}{b}}$$

as:

‘$\,A\,$ is to $\,a\,$ as $\,B\,$ is to $\,b\,$’

Cross-multiplying is a useful technique whenever you find yourself working with proportions:

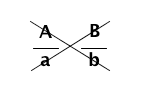
DEFINITION cross-multiplying

The process of going from the proportion $$\cssId{s77}{\frac{A}{a} = \frac{B}{b}}$$ to the equivalent statement $$\cssId{s79}{Ab = aB}$$ is called cross-multiplying.

Cross-multiplying is nothing other than an application of the Multiplication Property of Equality, where both sides of the equation are multiplied by the product of the original denominators: $$ \begin{gather} \cssId{s83}{\frac{A}{a} = \frac{B}{b}}\cr\cr \cssId{s84}{\frac{A}{a}\cdot (ab) = \frac{B}{b}\cdot (ab)}\cr\cr \cssId{s85}{Ab = Ba} \end{gather} $$

DEFINITION the phrase: ‘corresponding sides are proportional’

Suppose a triangle with sides $\,a\,,$ $\,b\,,$ and $\,c\,$ is scaled to get a new triangle with corresponding sides $\,A\,,$ $\,B\,,$ and $\,C\,.$

In this situation, the phrase corresponding sides are proportional is used to describe the equality of ratios:

$$ \cssId{s90}{\frac{A}{a} = \frac{B}{b} = \frac{C}{c}} $$

This same terminology is used when scaling any polygon.

Finally, we are ready for the precise definition of similar polygons:

DEFINITION similar polygons

Two polygons are similar if and only if there exists a correspondence between their vertices such that corresponding sides are proportional and corresponding angles are equal.

In general, to prove that two polygons are similar, you must check two different things:

that corresponding angles are equal
that corresponding sides are proportional

It is an extremely useful result that for triangles (and triangles alone!) it suffices to check only that angles are equal; you then get the corresponding sides proportional for free. Of course, if two angles are equal, then the third angles must be equal, and so we have the (unproved) theorem:

AA SIMILARITY THEOREM

Two triangles are similar if and only if two angles of one triangle are equal to two angles of the other triangle.

This is not true for polygons other than triangles. For example, look at the pictures below. All the angles are the same, but the polygons are not similar.