|
Create a Child for Wolf
To fully illustrate new concepts, we need Wolf to have a child:
|
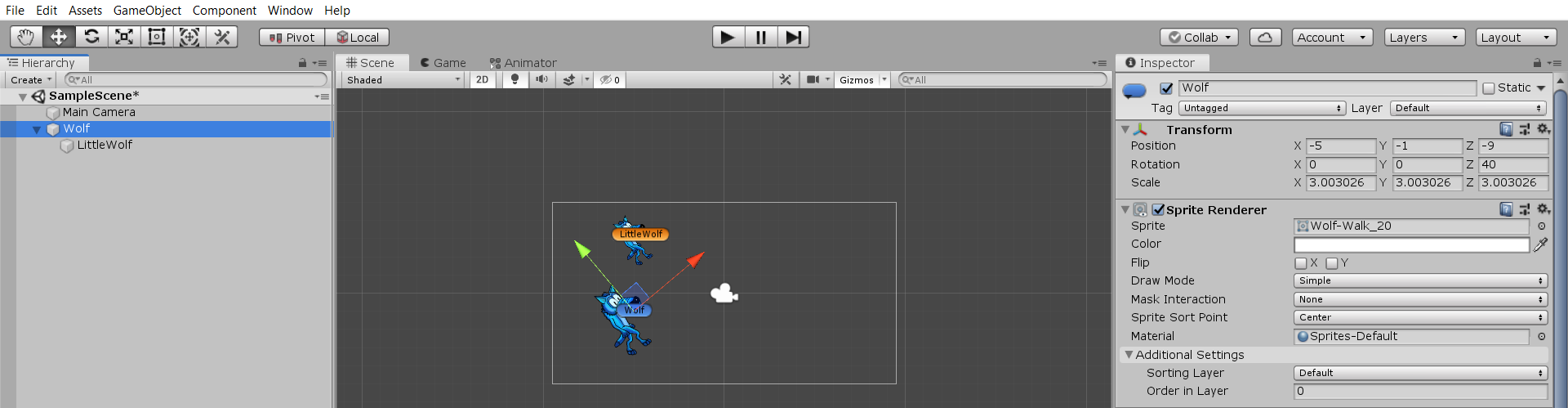 (1a) create a child for 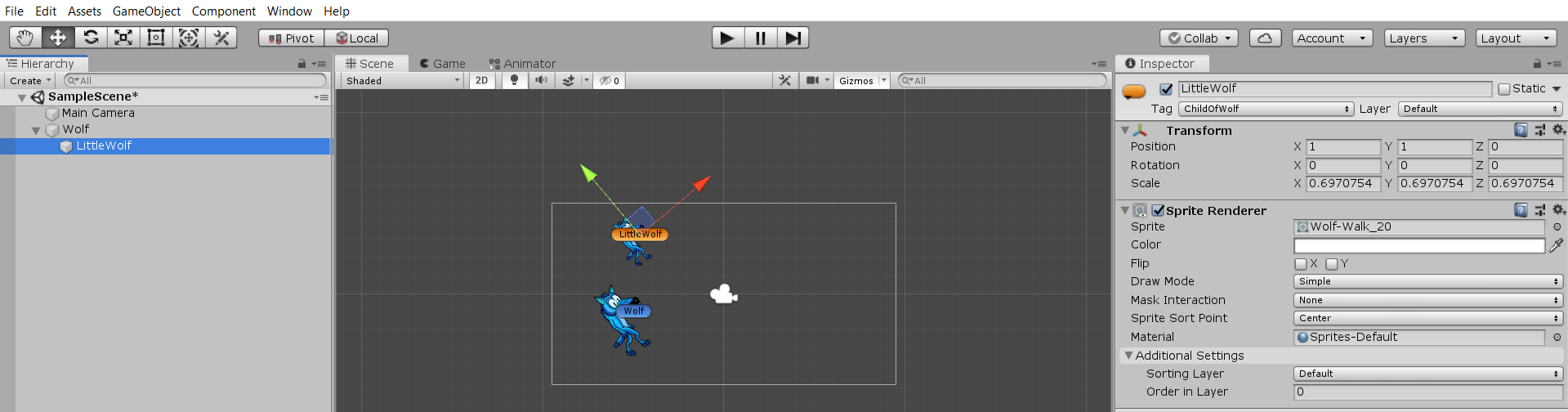 (1b) settings for |
|
Create a Child for Wolf
To fully illustrate new concepts, we need Wolf to have a child:
|
 (1a) create a child for  (1b) settings for |
|
Rectangular Coordinate Systems
Quantifying (i.e., assigning numbers to) any movement/position requires a coordinate system.A coordinate system uses one or more numbers (usually called coordinates) to uniquely determine position. The most common type of coordinate system is a rectangular coordinate system. A rectangular coordinate system consists of intersecting number lines (called the axes) that are perpendicular to each other. The single point that all axes have in common is called the origin of the rectangular coordinate system. It's important to note that every number line has a specified unit, determined by the distance between (say) $\,0\,$ and $\,1\,.$ By knowing where is $\,1\,$ located in relation to $\,0\,,$ every real number can then be uniquely positioned on the number line. Thus, every rectanglar coordinate system has these vital components (see (1) at right):
Together, the axes/origin/units allow you to uniquely position any point. The entire set of ‘coordinate-endowed’ points is often called a ‘space’. Situations That Use More Than One Rectangular Coordinate System
Sometimes (like in Unity game development!) you find yourself in a situation whereIn such cases, you ‘Relative To’
The phrase ‘relative to’ is used in the context of ‘competing’ coordinate systems.‘Relative to ...’ means ‘using the axes/origin/units of ...’ Here's an example. Let's name two different 2D rectangular coordinate systems $\,A\,$ and $\,B\,.$ See (2) at right. Either coordinate system equally well assigns unique ‘names’ to every point in the plane. However, points get different names, depending on which coordinate system we use. Consider the coordinates $\,(1,2)\,.$ To plot this point relative to $\,A\,$:
|
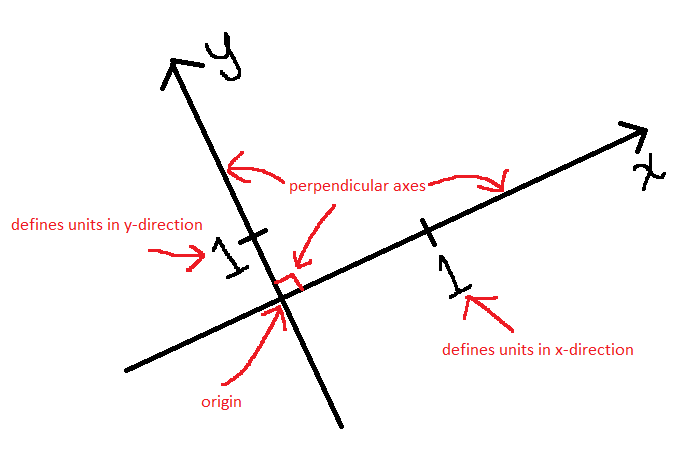 (1) common features of a rectangular coordinate system 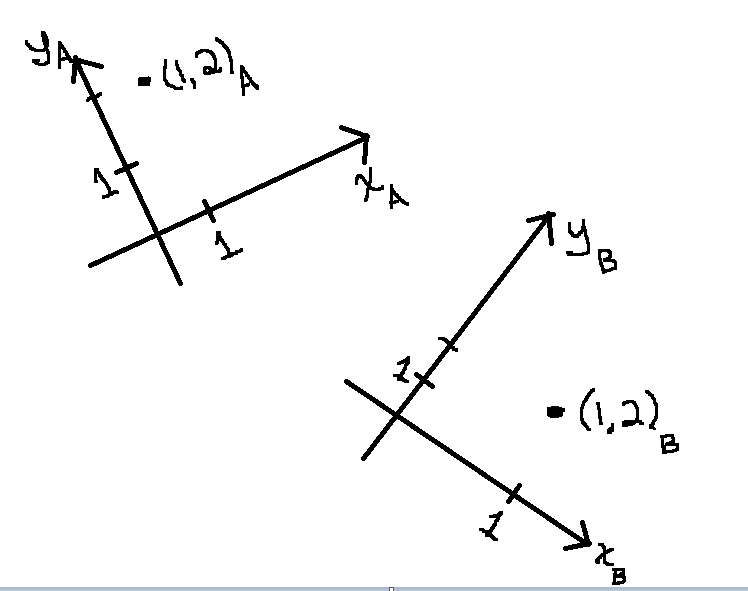 (2) plotting points relative to different coordinate systems |
| If you rotate a GameObject via its fields, then that GameObject's Object Space origin is the pivot point for the rotation. See (2de) at right. |
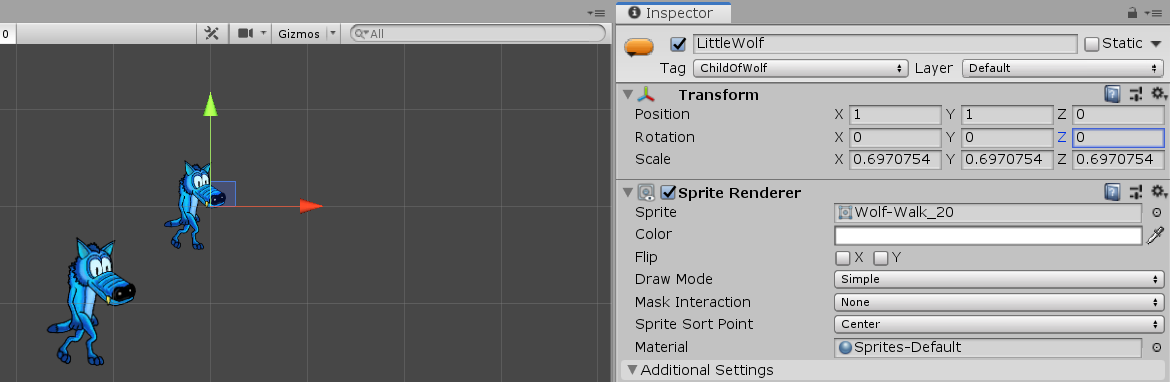 (2d) LittleWolf, before rotation |
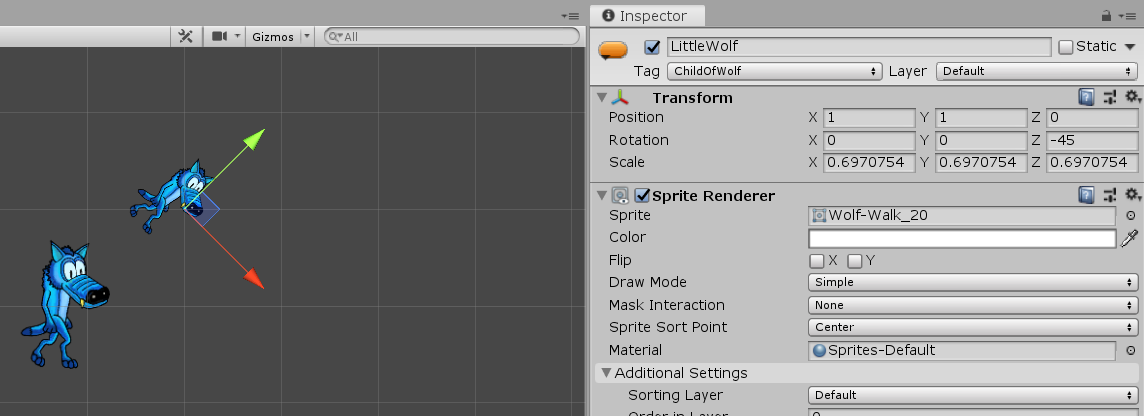 (2e) LittleWolf, after a $\,-45^\circ\,$ rotation |
|
A GameObject's Object Space can't be used to position itself, since
Object Space moves with its GameObject. A GameObject's Object Space is vitally important to the GameObject's children (and children of children, etc.) Keep reading! |
The table below gives some sample calculations.
Verify these calculations (as desired) in the Unity Engine, or just study the table.
The scale values in this table will distort your sprites; they are merely for illustrative purposes.
All GameObject rotations have been set to $\,(0,0,0)\,,$ to simplify calculations.
| GameObject | info | Transform-Position values |
Transform-Scale values |
World Space Coordinates |
| Wolf | top level | (1a) $$(-5,-1,-9)$$ | (2a) $$(3\,,\,2\,,\,1)$$ | (3a) $$(-5,-1,-9)$$ |
| LittleWolf | child of Wolf |
(1b)
$$(1.5\,,\,0.5\,,\,0)$$
|
(2b) $$(0.6\,,\,0.7\,,\,0.8)$$ |
(3b) Below, the $\,\color{red}{\bigstar}\,$ operation between (2a) and (1b) denotes component-by-component multiplication. $$ \begin{align} \text{(3a)} \ &+\ \text{(2a)}\color{red}{\bigstar}\text{(1b)}\cr &= (-5,-1,-9) + (3\,,\,2\,,\,1)\color{red}{\bigstar} (1.5\,,\,0.5\,,\,0)\cr &= (-5,-1,-9) + (3\cdot 1.5\,,\, 2\cdot 0.5\,,\, 1\cdot 0)\cr &= (-5,-1,-9) + (4.5\,,\,1\,,\,0)\cr &= (-5+4.5\,,\, -1+1\,,\, -9+0)\cr &= (-0.5\,,\,0\,,\,-9) \end{align} $$ |
| LittlestWolf | child of LittleWolf |
(1c)
$$(1\,,\,1\,,\,1)$$
|
$$ \text{not needed} $$ | $$ \begin{align} \text{(3b)} \ &+\ \text{(2a)}\color{red}{\bigstar}\text{(2b)}\color{red}{\bigstar}\text{(1c)}\cr &= (-0.5\,,\,0\,,-9) + (3\,,\,2\,,\,1)\color{red}{\bigstar} (0.6\,,\,0.7\,,\,0.8)\color{red}{\bigstar}(1\,,\,1\,,\,1)\cr &= (-0.5\,,\,0\,,-9) + (3\cdot 0.6\cdot 1\,,\, 2\cdot 0.7\cdot 1\,,\, 1\cdot 0.8\cdot 1)\cr &= (-0.5\,,\,0\,,-9) + (1.8\,,\,1.4\,,\,0.8)\cr &= (-0.5+1.8\,,\, 0+1.4\,,\, -9+0.8)\cr &= (1.3\,,\,1.4\,,\,-8.2) \end{align} $$ |

transform.position
transform.position always returns the World Space coordinates of any GameObject.Use the table above to set and and values. Write the script shown in (1a), and pull it onto . Note that in line 11, tag is used to ‘find’ . See (1b) at right for the script output. The World Space coordinates for are indeed as predicted! |
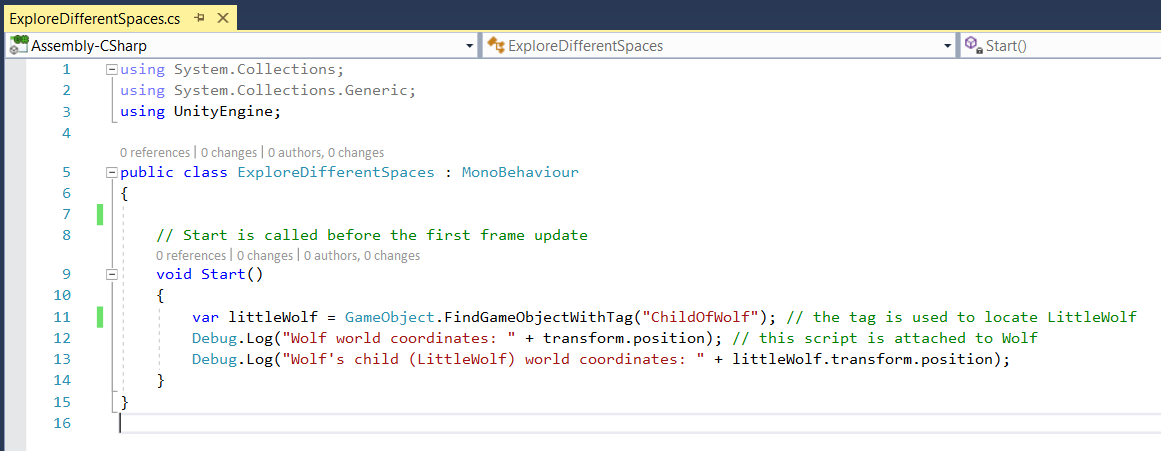 (1a) script to explore world coordinates for parent () and child () a text file containing this ExploreDifferentSpaces code 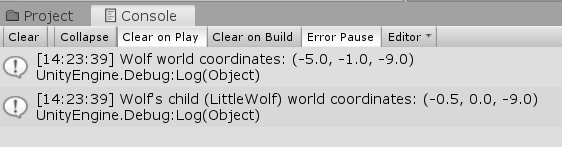 (1b) output from the code above |
|
Understanding Frame Rate Dependence
The units of our
previously-coded motion
are ‘WorldUnits per frame’.However, Unity frame rate is not constant:
Time.deltaTimeTime.deltaTime gives the time (in seconds) between the current frame and the previous frame.The current frame rate (which changes from frame-to-frame) is: $$\text{current frame rate} \ =\ \frac{1}{\text{Time.deltaTime}}$$ The simple program in (1) at right will help you explore: number of frames rendered per second during Unity game play? Below (2a–2c) are some console snapshots after I dragged onto Wolf, and then played the game: |
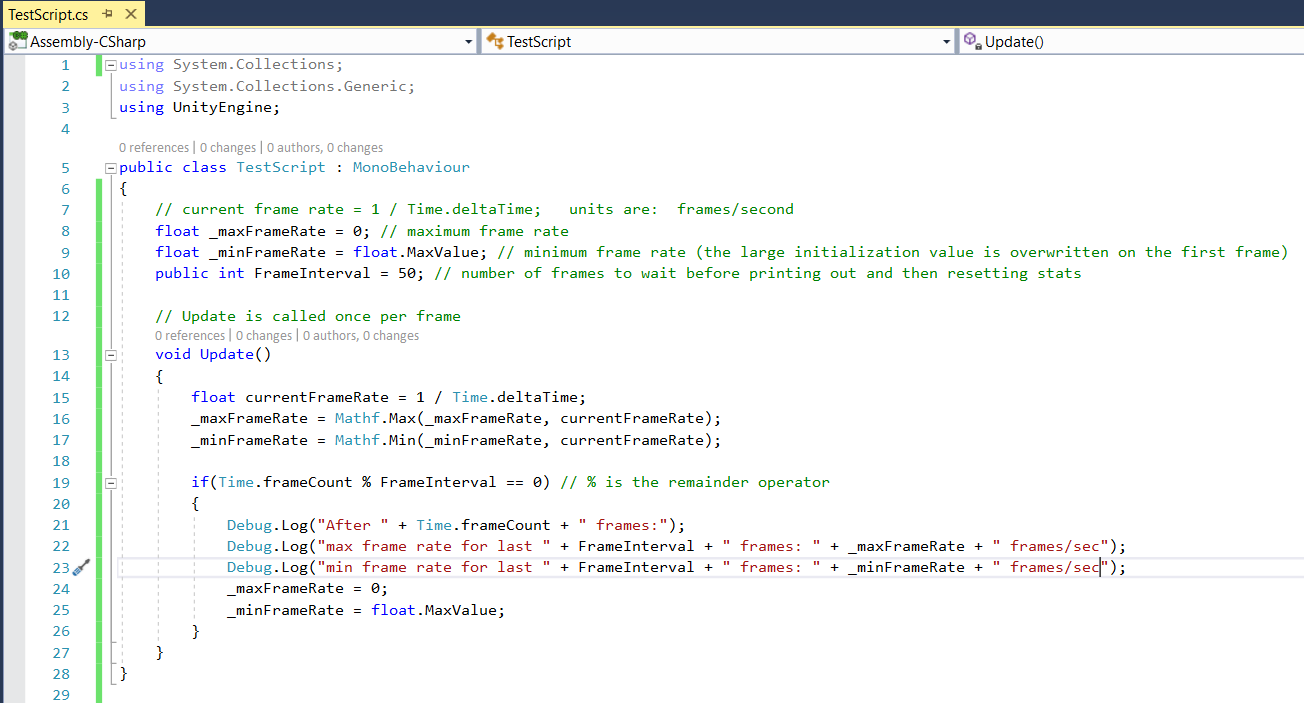 (1) code to better understand frame rate and Time.deltaTimea text file containing this TestScript code |
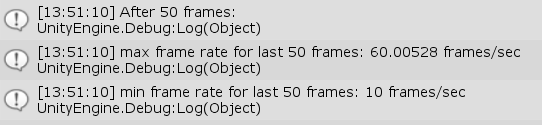 (2a) There is some ‘start-up’ slowness. |
 (2b) With nothing much going on, the frame rate was fairly constant for me. |
 (2c) I started playing a DVD to ‘stress’ the system. |
|
ILSpy
For experts only:Ray uses ILSpy to decompile C# code. Among other things, it shows the actual code that defines built-in methods. Notes on the Program in (1)
In what follows, green entries specialize concepts to
the code shown in (1).
|
var’ Keyword; Implicitly-Typed Variablesvar keyword is short for ‘variable’.var i = 5;int (integer) type.
var x = 5f;float type.
var keyword is called an implicitly-typed variable.var’var keyword.|
More Vector Concepts
Below is C# code to further understand uniform motion (and practice C# coding).To achieve uniform speed for movement in any direction, we need a few more vector concepts. If you want a complete discussion of vectors, start here in my online Precalculus course. Vector Magnitude; Unit Vectors
Let $\,(x,y,z)\,$ be a three-dimensional vector. (A similar discussion holds for two-dimensional vectors.)The magnitude of $\,(x,y,z)\,$ is the square root of the sum of the squares of its components. The magnitude gives the length of the arrow representing the vector. $$ \text{magnitude of the vector $\,(x,y,z)\,$ is: } \ \ \sqrt{x^2 + y^2 + z^2} $$ A vector with magnitude $\,1\,$ is called a unit vector. Note that $\,(1,0,0)\,$ and $\,(-1,0,0)\,$ are both unit vectors, since: $$ \sqrt{\strut 1^2 + 0^2 + 0^2} = 1\ \ \ \ \text{ and }\ \ \ \ \sqrt{\strut(-1)^2 + 0^2 + 0^2} = 1 $$ For convenience, Unity defines the following unit vectors:
Normalizing a Vector
If you take any vector and divide by its length, then a unit vector results.The process of dividing by the length (and thus achieving a unit vector) is called normalizing the vector. In C# scripts, if myVector is any vector (2D or 3D),
then myVector.normalized is a unit vector that points in the same direction.For example, $\,(-3,2,1)\,$ normalizes to (approximately) $\,(-0.802,0.535,0.267)\,$: $$ \sqrt{(-0.802)^2 + (0.535)^2 + (0.267)^2} \ \approx\ 1 $$ (WolframAlpha is a great online resource for computations!) |
|
Getting a Direction Vector from Point $\,A\,$ to Point $\,B\,$
Let $\,A(x_A,y_A)\,$ and $\,B(x_B,y_B)\,$ be points.Then, $\,B - A = (x_B - x_A\,,\,y_B - y_A)\,$ is a vector from $\,A\,$ to $\,B\,.$ The same thing works in 3D. This is an immediate consequence of vector addition, as follows. Travel from the origin to $\,B\,$ (the desired destination) in two different ways:
just take your destination point, and subtract your starting point. |
|
Going From a 2D Vector to an Angle Representing the Vector's Direction
Take a 2D vector $\,(x,y)\,$ and put its tail at the origin, as in (2ab) at right.The vector then naturally lies in one of the four quadrants (or on an axis). We will need to know the angle between the positive $\,x\,$-axis and the vector (denoted by $\,\theta\,$ at right). Fortunately, Unity (making good use of the arctangent function) gives an easy way to go from vector coordinates $\,(x,y)\,$ to a convenient angle representing its direction. For a given vector (x,y) :Mathf.Atan2(y,x)
returns an angle
that
represents the direction the vector is pointing
|
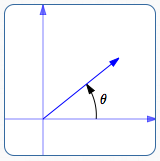 (2a) For vectors (x,y) in quadrants I and II, Mathf.Atan2(y,x)returns positive angles. |
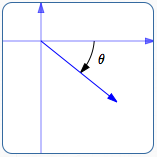 (2b) For vectors (x,y) in quadrants III and IV, Mathf.Atan2(y,x)returns negative angles. |
Here are details on Mathf.Atan2(y,x) :
|
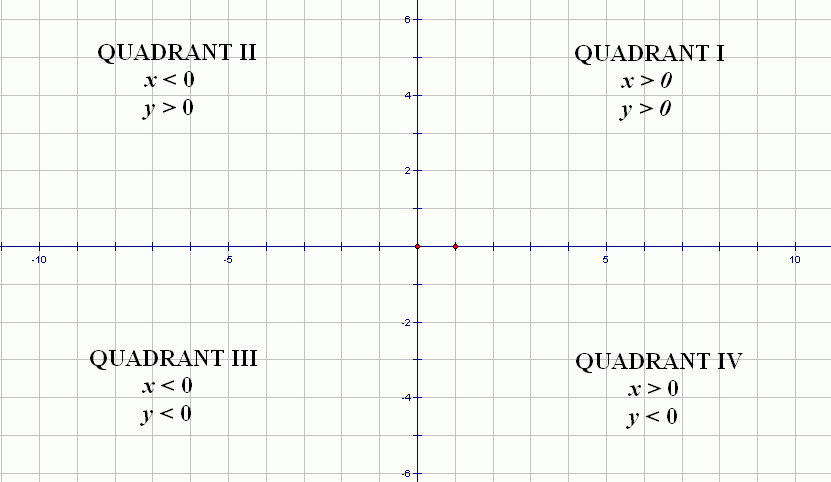 (3) the four quadrants |
|
C# Code for Uniform Motion in Any Direction
Create a new script, as shown at right.Drag the script onto . Only new or notable code features are discussed here:
|
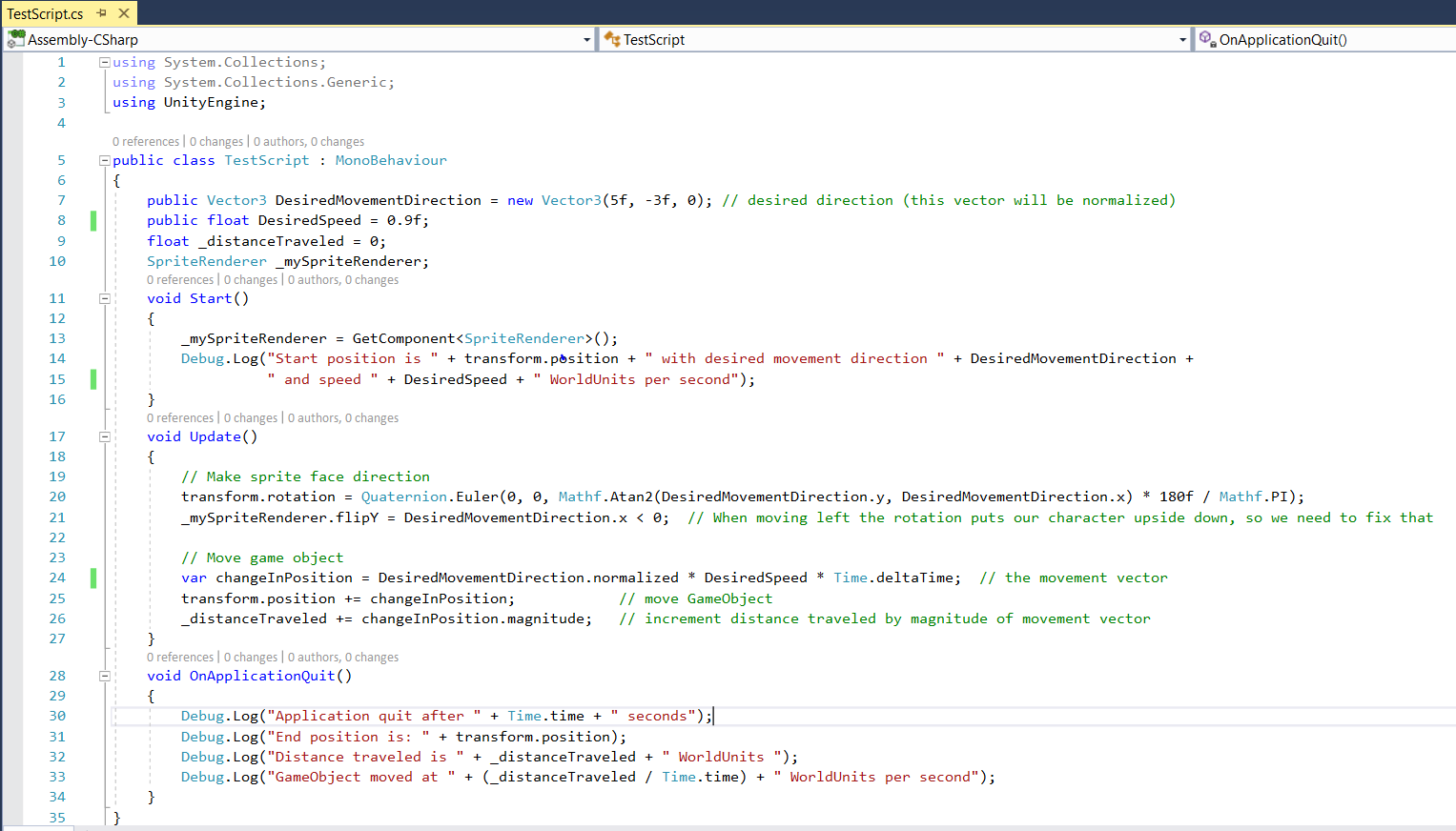 (1) move with uniform speed in a desired direction a text file containing this TestScript code 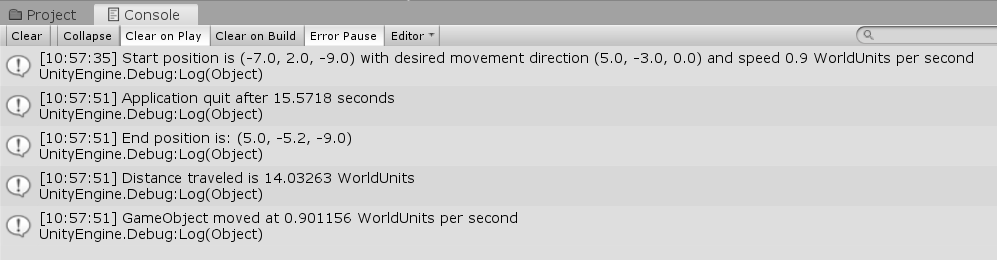 (2) console output from above code |
So, here are details on how line 21 behaves:
Analyzing the Code Output
Let's look at the console output, shown in (2) at right.All movement is done in 2D, so we can ignore the $\,z\,$ coordinate. The distance between the start point $\,(-7,2)\,$ and the end point $\,(5.0,-5.2)\,$ is: $$ \sqrt{(5-(-7))^2 + (-5.2-2)^2} \ \approx\ 14 $$ Since distance equals rate times time ($\,d = rt\,$), we have $$ \begin{gather} r = \frac{d}{t}\cr\cr r = \frac{14.03263}{15.5718} \approx 0.901156 \end{gather} $$ Not bad in matching the target speed of $\,0.9\,$! |