Inverse Trigonometric Function Problems: All Mixed Up

Thanks for your support!

 

Compute:   $\,\arcsin ( \sin 210^\circ)$

Solution:
Caution! Since the sine and arcsine functions are not true inverses, they do not necessarily ‘undo’ each other.
Indeed, $\,\arcsin( \sin 210^\circ)\,$ cannot equal $\,210^\circ\,,$ since the arcsine always returns an angle between $\,-90^\circ\,$ and $\,90^\circ\,.$

Work from the ‘inside’ of the expression to the ‘outside’: $$\cssId{s14}{ \overset{\text{step 3}} {\overbrace{\arcsin (\ \underset{\text{step 2}} { \underbrace{\sin \overset{\text{step 1}} {\overbrace{210^\circ}} }}\ )}}} $$

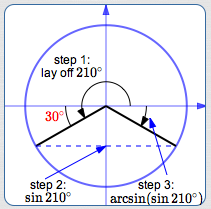
Step 1:	As shown at right, lay off a $\,210^\circ\,$ angle ($\,210^\circ = 180^\circ + 30^\circ\,$) in the unit circle. Recall that positive angles are laid off in a counterclockwise direction. Observe that the reference angle for $\,210^\circ\,$ is $\,\color{red}{30^\circ}\,.$
Step 2:	By definition of the sine function, $\,\sin 210^\circ\,$ is the $y$-value of the terminal point.
Step 3:	Apply the arcsine function: What angle between $\,-90^\circ\,$ and $\,90^\circ\,$ has this $y$-value? Answer: $\,-30^\circ$
Report the answer:	$\arcsin(\sin 210^\circ) = -30^\circ$

Example 2

Find:   $\,\tan(\arcsin \frac 45)\,$

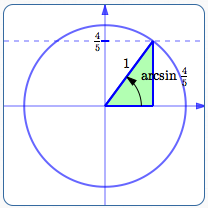
Step 1:	Show the angle   $\,\arcsin \frac{4}{5}\,$   on a unit circle. It is the unique angle between $\,-90^\circ\,$ and $\,90^\circ\,$ whose sine value is $\,\frac 45\,$; i.e., the unique angle (in the first quadrant) whose terminal point has $y$-value equal to $\,\frac 45\,.$
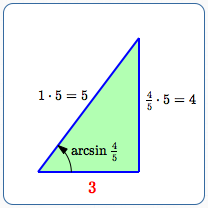
Step 2:	Take the green triangle (which has hypotenuse of length $\,1\,$ and vertical side of length $\,\frac 45\,$) and multiply all the side lengths by $\,5\,.$ This gives a similar triangle with side lengths that are much easier to work with! Alternative approach for steps 1 and 2: use the right triangle approach only: sine is opposite over hypotenuse draw a right triangle with an acute angle labeled $\,\arcsin \frac 45\,$ mark lengths on the opposite side and hypotenuse, using: $\,\text{sine} = \frac 45 = \frac{\text{OPP}}{\text{HYP}}$
Step 3:	Compute the remaining side length in the triangle: immediately recognize the special $\,\color{red}{3}{-}4{-}5\,$ right triangle or: use the Pythagorean theorem: $\,x^2 + 4^2 = 5^2\,,$   so $\,x = \color{red}{3}\,$
Step 4:	Tangent is opposite over adjacent:   $ \displaystyle\tan(\arcsin \frac 45) = \frac{\text{OPP}}{\text{ADJ}} = \frac 43 $

Example 3

Rewrite as an algebraic expression in $\,t\,$:   $\,\tan(\arcsin t)\,$

This is similar to the prior example, except for the variable $\,t\,$ instead of the constant $\,\frac 45\,.$
For what values of $\,t\,$ is $\,\arcsin t\,$ defined?   In other words, what is the domain of the arcsine function?   Answer:   $\,t\in[-1,1]\,$

Initially, we'll suppose that $\,0 < t < 1\,,$ so you can see the similarity to the prior example.
Then, we'll see that the formula obtained also works for $\,t = 0\,$ and $\,-1 < t < 0\,.$
Since both $\,\tan(\arcsin 1) = \tan(90^\circ)\,$ and $\,\tan(\arcsin(-1)) = \tan(-90^\circ)\,$ do not exist,
the expression $\,\tan(\arcsin t)\,$ is not defined at $\,t = \pm 1\,.$

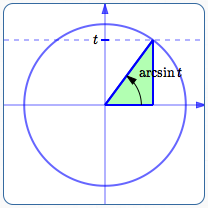
Step 1:	Let $\,0 < t < 1\,.$ Show the angle   $\,\arcsin t\,$   on a unit circle. It is the unique angle between $\,-90^\circ\,$ and $\,90^\circ\,$ whose sine value is $\,t\,$; i.e., the unique angle (in the first quadrant) whose terminal point has $y$-value equal to $\,t\,.$
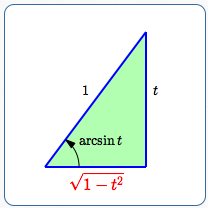
Step 2:	Or, use the right triangle approach: sine is opposite over hypotenuse, so $$ \cssId{s66}{\text{sine} = t = \frac {t}{1} = \frac{\text{OPP}}{\text{HYP}}} $$ Mark the opposite side as $\,t\,$ and the hypotenuse as $\,1\,.$
Step 3:	Compute the remaining side length in the triangle: $$ \begin{gather} \cssId{s70}{x^2 + t^2 = 1^2}\cr \cssId{s71}{x^2 = 1 - t^2}\cr \cssId{s72}{x = \pm\sqrt{1 - t^2}} \end{gather} $$ Since $\,x > 0\,$ in this initial discussion, choose the ‘$+$’ sign.
Step 4:	Tangent is opposite over adjacent:   $ \displaystyle\tan(\arcsin t) = \frac{\text{OPP}}{\text{ADJ}} = \frac{t}{\sqrt{1-t^2}} $
Step 5:	Note that the formula also works for $\,t = 0\,,$ as follows: $\tan (\arcsin 0) = \tan 0 = 0$ for $\,t = 0\,,$ $\frac{t}{\sqrt{1-t^2}} = \frac{0}{\sqrt{1 - 0^2}} = 0$
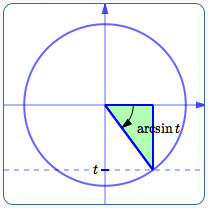
Step 6:	Note that the formula also works for $\,-1 < t < 0\,,$ as follows: In this case, $\,\arcsin t\,$ is in Quadrant IV. In Quadrant IV, the tangent is negative. The size of $\,\tan (\arcsin t)\,$ is the same as in Quadrant I. So, we want a formula that has the same size as $\,\frac{t}{\sqrt{1-t^2}}\,$ and is negative. Note that when $\,t\,$ is negative, so is $\,\frac{t}{\sqrt{1 - t^2}}\,$ (since it has a negative numerator and a positive denominator). Together, $\,\tan (\arcsin t) = \frac{t}{\sqrt{1-t^2}}\,$ for $\,-1 < t < 0\,.$
Step 7:	Combining all the cases: $$ \cssId{s92}{\tan (\arcsin t) = \frac{t}{\sqrt{1 - t^2}}\ \ \ \text{for}\ \ \ -1 \lt t\lt 1} $$

If you only need a reliable answer ...

Zip up to WolframAlpha and type in:

arcsin ( sin(210 deg) )

tan( arcsin (4/5) )

tan( arcsin t )

Master the ideas from this section
by practicing the exercise at the bottom of this page.

When you're done practicing, move on to:
Solving Trigonometric Equations