Inverse Trigonometric Function: Arccosine (Part 1)

(This page is Part 1. Click here for Part 2.)

Before studying this section, you are encouraged to read Trying to ‘Undo’ Trigonometric Functions.

This section is a copy of Inverse Trigonometric Function: Arcsine, with appropriate changes. If you've mastered the arcsine section, then this one should be quick and easy!

The arccosine function was informally introduced in Using the Law of Cosines in the SSS case (& Introduction to the Arccosine Function) . It is made precise here.

For a function to have an inverse, each output must have exactly one corresponding input. Thus, only one-to-one functions have inverses.

The cosine function doesn't have a true inverse, because the cosine function is not one-to-one. So, to try and define an ‘inverse cosine function’, we do the best we can.

We throw away most of the cosine curve, leaving us with a piece that has three properties:

• the piece is one-to-one (and hence has an inverse)
• the piece covers all the outputs from the cosine function (the interval $\,[-1,1]\,$)
• the piece is close to the origin

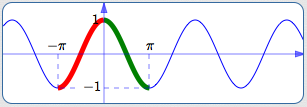
The cosine curve has two pieces that meet all three requirements:

• the green piece shown above
• the red piece shown above

The green piece is nicer, because it has positive $x$-values. Positive numbers are easier to work with than negative numbers. This green piece is the restriction of the cosine curve to the interval $\,[0,\pi]\,.$

The function that the mathematical community calls ‘the inverse cosine function’ is not actually the inverse of the cosine function, because the cosine function doesn't have a true inverse. Instead, the ‘inverse cosine function’ is the inverse of this green piece of the cosine curve.

Several Cycles of the Graph of the Cosine Function

The cosine function isn't one-to-one; it doesn't pass a horizontal line test. So, it doesn't have a true inverse.

To define an ‘inverse cosine function’, we do the best we can. Throw away most of the curve—leave only the green part.

This green part is one-to-one. This green part does have an inverse.

The inverse of this green part is what the mathematical community calls ‘the inverse cosine function’.

The arccosine function (precise definition below) is the best we can do in trying to get an inverse of the cosine function. The arccosine function is actually the inverse of the green piece shown above!

Here's a ‘function box’ view of what's going on:

The cosine function takes a real number as an input. It gives an output in the interval $\,[-1,1]\,.$

For example (as below), the output $\,0.5\,$ might come from the cosine function.

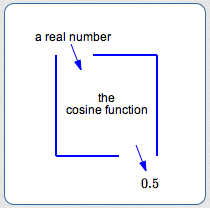
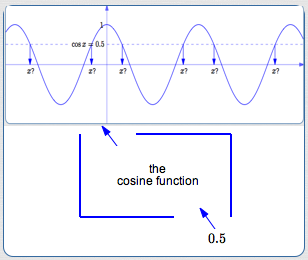
When we try to use the cosine function box ‘backwards’, we run into trouble.

The output $\,0.5\,$ could have come from any of the inputs shown.

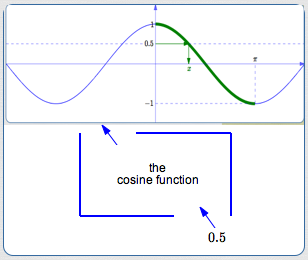
However, when we use the green piece of the cosine curve, the problem is solved!

Now, there's only one input that works. (It's the value of the green $\,\color{green}{x}\,.$ )

Observe that $\,\color{green}{x}\,$ is in the interval $\,[0,\pi]\,.$

It's a bit of a misnomer, but the arccosine function (precise definition below) is often referred to as the ‘inverse cosine function’. A better name would be something like ‘the inverse of an appropriately-restricted cosine function’. (It's no surprise, however, that people don't say something that long and cumbersome.)

So, what exactly is $\,\arccos 0.5\,$?

What Exactly is $\,\arccos x\,$?

More generally, let $\,x\,$ be any number in the interval $\,[-1,1]\,.$ Then:

In my own mind (author Dr. Carol Burns speaking here), the words I say are:

I personally know the endpoints are included, so this doesn't confuse me. However, the word ‘between’ is ambiguous—it can include the endpoints or not, depending on context. It can be clarified by saying:

... but then it loses its simplicity. Ah—issues with language. Choose words that work for you!

Precise Definition of the Arccosine Function

The precise definition of the arccosine function follows. It can look a bit intimidating—the notes following the definition should help.

Notes on the Definition of the Arccosine Function

Understanding the Definition

The definition precisely answers the question: ‘What is the number $\,\arccos x\,$?’ Here's how:

Recall that ‘ if and only if ’ means the same thing as is equivalent to. Equivalent sentences have identical truth values:  if one is true, so is the other;  if one is false, so is the other.

Thus, if the sentence  ‘$\,y = \arccos x\,$’  is true, then the compound sentence

must also be true.

If  ‘$\,y = \arccos x\,$’  is true, then ‘$\,y\,$’ is just another name for ‘$\,\arccos x\,$’.

If  ‘$\,y = \arccos x\,$’  is true, then two things must be true about $\,\arccos x\,$ (i.e., $\,y\,$):

• $\cos \overbrace{y}^{\arccos x} = x\,$:  its cosine must be $\,x$
• $0 \le \overbrace{y}^{\arccos x}\le \pi\,$:  it must be in the interval $\,[0,\pi]$

Combining these ideas:

That is: