 Graphing Hyperbolas
(Part 1)
Graphing Hyperbolas
(Part 1)
(This page is Part 1. Click here for Part 2.)
Hyperbolas were introduced in three prior lessons:
The purpose of this current section is to go from the equation of a hyperbola to its graph. In particular, we'll see that every hyperbola has a so-called central box that is helpful in determining its shape.
Short on time? Jump right to the summary!
This lesson includes lots of details. Once you understand things, it can be written more compactly.
For your convenience, the standard equations of hyperbolas (that were derived in the preceding section) are repeated here:
Equations of Hyperbolas: Center at the Origin
In both equations, $\,a \gt 0\,$ and $\,b \gt 0\,.$
Also, $\,c\,$ is the positive number for which $\,c^2 = a^2 + b^2\,.$
With the equations in standard form, $\,a^2\,$ is the denominator of the positive term on the left side.
Foci on the $x$-axis
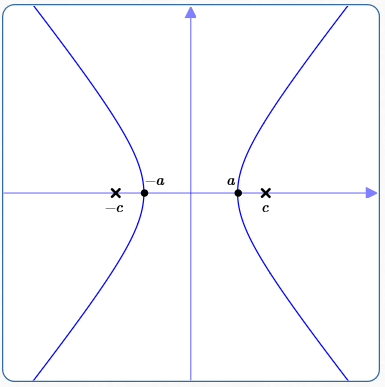 $$\cssId{s17}{\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1}$$
$$\cssId{s17}{\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1}$$
Vertices: $\,(-a,0)\,$ and $\,(a,0)$
Foci: $\,(-c,0)\,$ and $\,(c,0)$
Foci on the $y$-axis
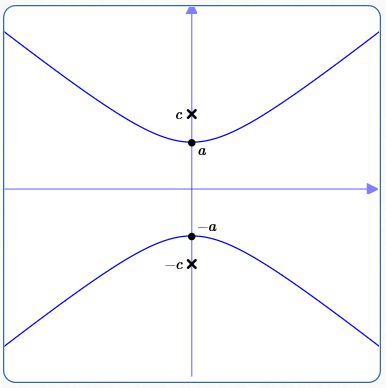 $$\cssId{s21}{\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1}$$
$$\cssId{s21}{\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1}$$
Vertices: $\,(0,-a)\,$ and $\,(0,a)$
Foci: $\,(0,-c)\,$ and $\,(0,c)$
Review
The following facts are used in this lesson:
The Square Root Function is Increasing
In particular, if $\,0 \le x \le y\,,$ then $\,0 \le \sqrt{x} \le \sqrt{y}\,.$
Renaming the Square Root of a Square
For all real numbers $\,x\,,$ $\sqrt{x^2} = |x|\,.$
The Absolute Value of a Nonnegative Number is Itself
If $\,x \ge 0\,,$ then $\,|x| = x\,.$
Squared Quantities are Nonnegative
For all real numbers $\,x\,,$ $\,x^2 \ge 0\,.$
Solving an Absolute Value Inequality
For all real numbers $\,x\,$ and for $\,k \gt 0\,$:
The Square Root of a Product is the Product of the Square Roots
Providing both $\,x\ge 0\,$ and $\,y\ge 0\,,$ then:
$$\sqrt{xy} = \sqrt{x}\,\sqrt{y}$$Solving an Absolute Value Equation
For all real numbers $\,x\,$ and for $\,k \ge 0\,$:
Important Information Given By the Equations of Hyperbolas
Many equations easily give you lots of information about their graphs, without any memorizing! This is certainly true with hyperbolas, as follows.
What Part of the Plane Do Hyperbolas Live In?
Let's rewrite and analyze the equation $\,\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\,$:
Thus:
$$ \cssId{s50}{\frac{x^2}{a^2}\ge 1} $$$$ \cssId{s51}{x^2\ge a^2} $$
Multiply both sides by $\,a^2 \gt 0$
Take note of this intermediate result: it follows that for any point on the hyperbola, $\,x^2 - a^2 \ge 0\,.$ We'll use this fact below.
Continuing:
$$ \cssId{s57}{\sqrt{\strut x^2} \ge \sqrt{\strut a^2}} $$The square root function is increasing
$$ \cssId{s59}{|x| \ge |a|} $$Since $\,\sqrt{x^2} = |x|$
$$ \cssId{s61}{|x| \ge a} $$Since $\,a \gt 0\,,$ $\,|a| = a$
$$ \cssId{s63}{x \ge a\ \ \ \text{ or }\ \ \ x\le -a} $$Solving the absolute value inequality
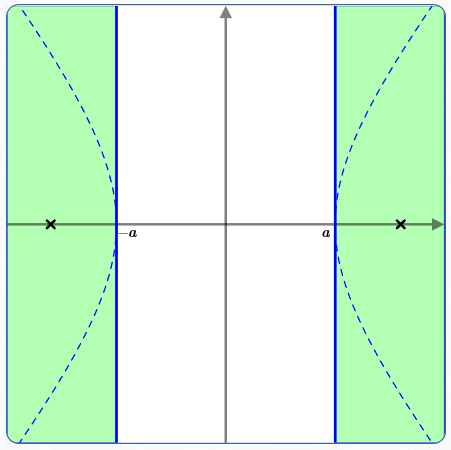
This confirms that any point $\,(x,y)\,$ satisfying $\,\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\,$ must lie in one of the two half-planes, $\,x \ge a\,$ or $\,x\le -a\,,$ shaded green below:
What Do Hyperbolas Look Like When $\,x\,$ is Big?
What happens to the graph of $\,\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\,$ for large values of $\,x\,$? To answer this question, first ‘re-name’ the equation by solving for $\,y\,$:
$$ \cssId{s69}{\frac{y^2}{b^2} = \frac{x^2}{a^2} - 1} $$Re-arrange
$$ \cssId{s71}{y^2 = b^2\left(\frac{x^2}{a^2} - 1\right)} $$Multiply both sides by $\,b^2$
$$ \cssId{s73}{y^2 = b^2\left(\frac{x^2}{a^2} - \frac{a^2}{a^2}\right)} $$Rename $\,1\,$ as $\,\frac{a^2}{a^2}$
$$ \cssId{s75}{y^2 = \frac{b^2}{a^2}(x^2 - a^2)} $$Factor out $\,\frac{1}{a^2}$
$$ \cssId{s77}{\sqrt{y^2} = \sqrt{\frac{b^2}{a^2}(x^2 - a^2)}} $$Take square roots of both sides
$$ \cssId{s79}{|y| = \sqrt{\frac{b^2}{a^2}(x^2 - a^2)}} $$Since $\sqrt{y^2} = |y|$
$$ \cssId{s81}{|y| = \sqrt{\frac{b^2}{a^2}} \sqrt{\strut x^2 - a^2}} $$As shown above, $\,x^2 - a^2\ge 0\,$ for all points on the hyperbola
$$ \cssId{s83}{|y| = \frac{b}{a}\sqrt{\strut x^2 - a^2}} $$Both $\,a \gt 0\,$ and $\,b \gt 0\,$
$$ \cssId{s85}{|y| = \frac{b}{a}\sqrt{\strut x^2\bigl(1 - \frac{a^2}{x^2}\bigr)}} $$Factor out $\,x^2\,$; we're exploring this equation for big $\,x\,$ right now, so $\,x\ne 0$
$$ \cssId{s87}{y = \pm\frac{b}{a}\sqrt{\strut x^2\bigl(1 - \frac{a^2}{x^2}\bigr)}} $$Solve the absolute value equation; notice that the prior right-hand side is nonnegative
This version of the equation might look harder than what we started with ($\,\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\,$), but it's better for understanding what happens when $\,x\,$ gets big.
Here's the key idea (which will be firmed up in Calculus):
More precisely:
As an example, let $\,x = 1000a\,.$ (Here, $\,x\,$ isn't particularly big—it's just one thousand times bigger than $\,a\,.$ ) Already, though:
$$\cssId{s100}{\frac{a^2}{x^2} = \frac{a^2}{(1000a)^2} = \frac{1}{1{,}000{,}000}}$$That's pretty close to zero!
When $\,x\,$ Gets Big...
So, here's what happens to the equation
$$y = \pm\frac{b}{a}\sqrt{\strut x^2\bigl(1 - \frac{a^2}{x^2}\bigr)}$$as $\,x\,$ gets big (big positive, or big negative):
As $\,x\,$ gets big, $\,\frac{a^2}{x^2}\,$ approaches $\,0\,.$
As $\,\frac{a^2}{x^2}\,$ approaches $\,0\,,$ $\,(1-\frac{a^2}{x^2})\,$ approaches $\,1\,.$
As $\,(1-\frac{a^2}{x^2})\,$ approaches $\,1\,,$ the expression $\,x^2(1-\frac{a^2}{x^2})\,$ looks more and more like $\,x^2\,.$
Thus, $\,y = \pm\frac{b}{a}\sqrt{\strut x^2\bigl(1 - \frac{a^2}{x^2}\bigr)}\,$ looks more and more like $\,y = \pm\frac{b}{a}\sqrt{x^2}\,,$ which simplifies to $\,y = \pm\frac{b}{a}|x|\,.$
It Cleans Up Even More!
This cleans up even more! Because of the ‘plus or minus’ sign, we can lose the absolute value. Here are the details:
If $\,x\ge 0\,,$ then $\,|x| = x\,.$ In this case, $\,y = \pm \frac{b}{a}|x|\,$ becomes $\,y = \pm \frac{b}{a}x\,.$
If $\,x \lt 0\,,$ then $\,|x| = -x\,.$ In this case, $\,y = \pm \frac{b}{a}|x|\,$ becomes $\,y = \pm \frac{b}{a}(-x) = \mp \frac{b}{a}x\,.$
‘$\,y = \pm \frac{b}{a}x\,$’ is a shorthand for ‘$\,y = \frac bax \ \text{ or } \ y = -\frac bax\,$’.
‘$\,y = \mp \frac{b}{a}x\,$’ is a shorthand for ‘$\,y = -\frac bax \ \text{ or }\ y = \frac bax\,$’.
The sentence ‘$\,A \text{ or } B\,$’ is equivalent to ‘$\,B\text{ or } A\,$’.
Thus, $\,y = \pm \frac{b}{a}|x|\,$ is equivalent to $\,y = \pm\frac bax\,.$
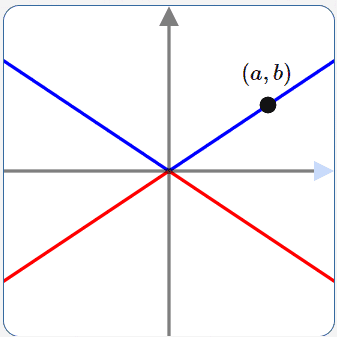
$y = \frac{b}{a}|x|\,$ is in blue
$y = -\frac{b}{a}|x|\,$ is in red
The entire graph (blue plus red) is $\,y = \pm\frac{b}{a}|x|\,.$
$y = \frac ba x\,$ is in blue
$y = -\frac ba x\,$ is in red
The entire graph (blue plus red) is $\,y = \pm \frac{b}{a}x\,.$