Definition of a Hyperbola

LESSON READ-THROUGH
by Dr. Carol JVF Burns (website creator)
Follow along with the highlighted text while you listen!
Thanks for your support!
 

Hyperbolas were introduced in Introduction to Conic Sections,
as one of several different curves (‘conic sections’) that are formed by intersecting a plane with an infinite double cone.

Identifying Conics by the Discriminant introduced the general equation for any conic section,
and gave conditions under which the graph would be a hyperbola.

In this current section, we present and explore the standard definition of a hyperbola.
This definition facilitates the derivation of standard equations for hyperbolas.

Recall that the notation ‘$\,d(P,Q)\,$’ denotes the distance between points $\,P\,$ and $\,Q\,.$

DEFINITION hyperbola
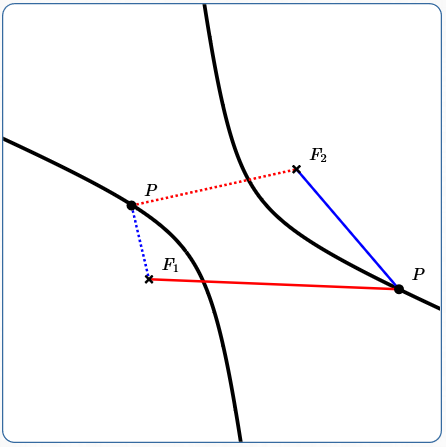
A hyperbola is the set of points in a plane such that the difference of the distances from two fixed points is constant.

More precisely:
  • Let $\,F_1\,$ and $\,F_2\,$ be distinct (different) points;
    they are called the foci of the hyperbola (pronounced FOE-sigh).
    (The singular form of ‘foci’ is ‘focus’.)
    Thus, $\,d(F_1,F_2)\,$ is strictly greater than zero.
  • Let $\,k\,$ be a positive real number, where $\,k < d(F_1,F_2)\,.$
    In this section, $\,k\,$ is referred to as the hyperbola constant.
The hyperbola determined by $\,F_1\,,$ $\,F_2\,$ and $\,k\,$ is the set of all points $\,P\,$ in a plane such that: $$ \cssId{s18}{\overbrace{\,\left|d(P,F_1) - d(P,F_2)\right|}^{\text{the difference of the distances to two fixed points}}} \quad \cssId{s19}{\overbrace{=\strut}^{\text{is}}}\quad \cssId{s20}{\overbrace{k}^{\text{constant}}} $$

$\,P\,$ is a general point on the hyperbola.

$|\,d(P,F_1) - d(P,F_2)| = \text{constant}$

$ \color{red}{\text{red (longer)}} - \color{blue}{\text{blue (shorter)}} = \text{constant} $

Notes on the Definition of a Hyperbola

Study the sketch at right as you read these notes.
  • Difference between two numbers:
    If you're asked for the difference between (say) the numbers $\,5\,$ and $\,7\,$ (or $\,7\,$ and $\,5\,$), then you automatically take the greater and subtract the lesser, giving $\,7 - 5 = 2\,.$ However, if asked for the difference between variables $\,a\,$ and $\,b\,,$ then you may not know which (if either) is greater! This is why the absolute value is needed in the definition of a hyperbola: $$ \cssId{s32}{\text{difference between $\,a\,$ and $\,b\,$} \ =\ |a - b| \ =\ |b - a|} $$
  • Hyperbola constant:
    Take any point $\,P\,$ on a hyperbola.
    Travel from $\,P\,$ to one focus, and record this distance.
    Travel from $\,P\,$ to the other focus, and record this distance.
    Take the larger recorded distance, and subtract the smaller.
    You'll always get the hyperbola constant, $\,k\,.$
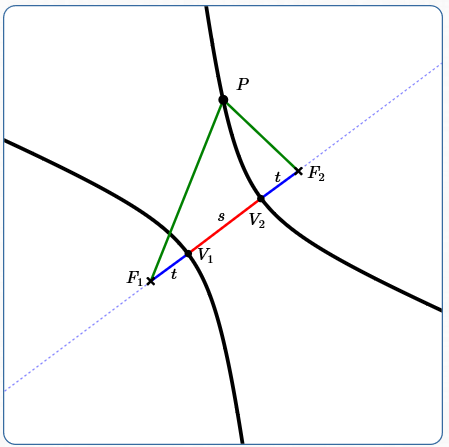
  • Major axis of a hyperbola:
    By definition, the line through the two foci is called the major axis of the hyperbola.
    The major axis is the dotted line in the image at right.
  • Vertices of a hyperbola:
    By definition, the points where a hyperbola intersects its major axis
    are called the vertices of the hyperbola.
    The singular form of ‘vertices’ is ‘vertex’.
    At right, the vertices are labeled $\,V_1\,$ and $\,V_2\,.$
  • Notation and an observation:
    Let $\,V_1\,$ and $\,V_2\,$ denote the vertices closest to $\,F_1\,$ and $\,F_2\,,$ respectively.
    Define $\,t_1 := d(V_1,F_1)\,$ and $\,t_2 := d(V_2,F_2)\,.$
    Define $\,s := d(V_1,V_2)\,,$ so $\,s\,$ is the length of the red segment at right.
    We must have $\,t_1 = t_2\,,$ as follows:
    Since $\,V_1\,$ is a point on the hyperbola: $$\begin{gather} \cssId{s52}{d(V_1,F_2) - d(V_1,F_1) = k}\cr \cssId{s53}{(s + t_2) - t_1 = k} \qquad \cssId{s54}{(*)} \end{gather} $$ Since $\,V_2\,$ is a point on the hyperbola: $$\begin{gather} \cssId{s56}{d(V_2,F_1) - d(V_2,F_2) = k}\cr \cssId{s57}{(s + t_1) - t_2 = k} \qquad \cssId{s58}{(**)} \end{gather} $$ Solving (*) and (**) simultaneously gives: $$ \begin{gather} \cssId{s60}{s + t_2 - t_1 = s + t_1 - t_2}\cr \cssId{s61}{2t_2 = 2t_1}\cr \cssId{s62}{t_2 = t_1} \end{gather} $$ Therefore, define $\,t := d(V_1,F_1) = d(V_2,F_2)\,,$ so $\,t\,$ is the length of each blue segment at right.
  • The hyperbola constant is the distance between the vertices:
    A hyperbola ‘shows’ its hyperbola constant as the distance between the two vertices.
    Why?
    Since $\,V_1\,$ is a point on the hyperbola with hyperbola constant $\,k\,,$ we have $$ \begin{gather} \cssId{s69}{d(V_1,F_2) - d(V_1,F_1) = k}\cr \cssId{s70}{(s+t) - t = k}\cr \cssId{s71}{\overbrace{\strut s}^{\text{distance between the vertices}} = \overbrace{\strut k}^{\text{hyperbola constant}}} \end{gather} $$

The line through the foci, $\,F_1\,$ and $\,F_2\,,$
is the major axis of the hyperbola.

The points $\,V_1\,$ and $\,V_2\,,$
where the major axis intersects the hyperbola,
are the vertices of the hyperbola.

A hyperbola ‘shows’ its hyperbola constant
as the distance between the vertices.

Playing with the Definition of a Hyperbola

You can play with hyperbolas using the dynamic JSXGraph at right:
  • $F_1\,$ and $\,F_2\,$ are the foci.
    They're plotted at right with the point-style .
    (To keep the graph uncluttered, they're not labeled.)
    Move them around!
    As you hover over each focus, you can see its coordinates.
  • The slider at the top sets the hyperbola constant.
    The slider can be set to numbers between $\,0\,$ and $\,20\,$ with increments of $\,0.5\,.$
    The starting value is $\,5\,$ (refresh the page as needed).
  • The current distance between the foci is displayed near the bottom.
    Watch this distance change as you move the foci around.
    The starting value for $\,d(F_1,F_2)\,$ is $\,10\,$ (refresh the page as needed).
  • In order to see a hyperbola, the hyperbola constant (slider value) must be strictly less than the distance between the foci.
  • $\,P\,$ is a general point on the hyperbola.
    $\,Q\,$ is a free point (it can be moved anywhere).
    Move them both around!
    The difference of their distances to the foci is shown at top/bottom.
  • When the hyperbola constant equals the distance between the foci, the ‘hyperbola’ degenerates to two rays.
  • When the hyperbola constant equals zero, the ‘hyperbola’ degenerates to the perpendicular bisector of the segment between the foci.

foci: $\,F_1\,$ and $\,F_2\,,$ marked with

vertices: marked in red

$\,P\,$:   a typical point on the hyperbola

$\,Q\,$:   a free point (can be moved anywhere)

An Analysis of the Hyperbola Constant

In the definition of hyperbola, the hyperbola constant $\,k\,$ is required to be positive,
and strictly less than the distance between the two foci: $$ \cssId{s106}{0 < k < d(F_1,F_2)} $$ Why?
As shown below, other values of $\,k\,$ don't give anything that a reasonable person would want to call a hyperbola!

$k < 0\,$:   No Points in the Solution Set

Absolute value is always nonnegative. That is, $\,|x| \ge 0\,$ for all real numbers $\,x\,.$
Therefore, if $\,k < 0\,,$ there are no points $\,P\,$ for which the hyperbola equation is true: $$ \cssId{s114}{\overbrace{\strut \,|d(P,F_1) - d(P,F_2)|}^{\,\ge\, 0\,} = \overbrace{\strut k}^{\lt \, 0} \qquad \text{ is always false }} $$

$k = 0\,$:   Perpendicular Bisector of Segment Between the Foci

The equation $\,|x| = 0\,$ is equivalent to $\,x = 0\,,$ for all real numbers $\,x\,.$
Thus, the following are equivalent: $$ \begin{gather} \cssId{s119}{|d(P,F_1) - d(P,F_2)| = 0}\cr\cr \cssId{s120}{d(P,F_1) - d(P,F_2) = 0}\cr\cr \cssId{s121}{d(P,F_1) = d(P,F_2)} \end{gather} $$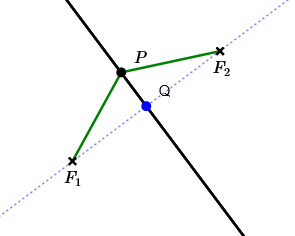 At right, $\,Q\,$ is the midpoint of the segment $\,\overline{F_1F_2}\,$ that connects the foci.
When $\,k = 0\,,$ the set of points satisfying the hyperbola equation is the perpendicular bisector of $\,\overline{F_1F_2}\,.$

A ‘TWO RAY’ HYPERBOLA:   $\,k = d(F_1,F_2)\,$

Suppose the hyperbola constant, $\,k\,,$ equals the distance between the foci.
That is, $\,k = d(F_1,F_2)\,.$

In this case, the solution set to the equation $$ \cssId{s129}{|\color{green}{d(P,F_1)} - \color{red}{d(P,F_2)}| = k} $$ is two rays, with $\,F_1\,$ and $\,F_2\,$ as endpoints, lying along the major axis.
This degenerate hyperbola is shown at right, in black.

$\,P\,$ is a point on the degenerate hyperbola; it can be dragged from one ray to the other.
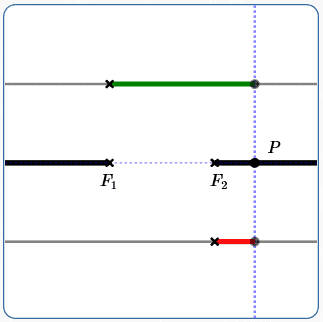
  • The black curve (two rays) is a degenerate hyperbola. It occurs when the hyperbola constant equals the distance between the foci.
  • $\,\color{green}{d(P,F_1)}\,$ is the length of the green segment
  • $\,\color{red}{d(P,F_2)}\,$ is the length of the red segment
  • The difference of these two lengths
    is the hyperbola constant, which (in this case)
    is the distance between the foci.

AN ‘EMPTY’ HYPERBOLA:   $\,k > d(F_1,F_2)\,$

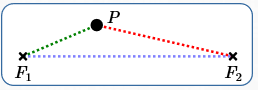
Suppose $\,F_1\,$ and $\,F_2\,$ are distinct points in a plane, and let $\,k > d(F_1,F_2)\,.$
Let $\,P\,$ be any point in the plane.

Switch names (if needed) so that $\,P\,$ is closer to $\,F_1\,$ (or equidistant from both foci). This situation is illustrated at right.

The shortest distance between any two points is a straight line.
In particular (refer to the sketch at right), traveling from $\,P\,$ to $\,F_1\,$,
and then from $\,F_1\,$ to $\,F_2\,$, must exceed (or equal) $\,\color{red}{d(P,F_2)}\,$: $$ \cssId{s150}{d(P,F_1) + d(F_1,F_2) \ge d(P,F_2)} $$ Re-arranging: $$ \cssId{s152}{d(P,F_2) - d(P,F_1) \le d(F_1,F_2)}\qquad \cssId{s153}{(*)} $$ We have: $$ \begin{alignat}{2} \cssId{s155}{|d(P,F_2) - d(P,F_1)|} &\ \cssId{s156}{=\ d(P,F_2) - d(P,F_1)} &\qquad &\cssId{s157}{\text{(for $\,x\ge 0\,,$ $\,|x| = x\,$)}}\cr &\ \cssId{s158}{\le\ d(F_1,F_2)}&&\cssId{s159}{\text{by (*)}}\cr &\ \cssId{s160}{< \ k}&&\cssId{s161}{\text{(by hypothesis)}} \end{alignat} $$ Consequently, there are no points $\,P\,$ for which the hyperbola equation is true: $$ \cssId{s163}{\overbrace{\strut \,|d(P,F_2) - d(P,F_1)|}^{\text{strictly less than $\,k\,$}} = k \qquad \text{ is always false }} $$ You might want to call this an empty hyperbola, an invisible hyperbola, or an imaginary hyperbola! There's nothing there!



Most people don't want to call any of these situations—the empty set, a line, or two rays—a hyperbola!
This is why these values for $\,k\,$ are not allowed in the definition of hyperbola.

Master the ideas from this section
by practicing the exercise at the bottom of this page.

When you're done practicing, move on to:
Equations of Hyperbolas in Standard Form


On this exercise, you will not key in your answer.
However, you can check to see if your answer is correct. 		PROBLEM TYPES:
1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16
AVAILABLE MASTERED
IN PROGRESS

(MAX is 16; there are 16 different problem types.)
Want textboxes to type in your answers? Check here: