Graphing Hyperbolas (Part 2)

(This page is Part 2. Click here for Part 1.)

Asymptotes for Hyperbolas

Asymptotes for $\,\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$

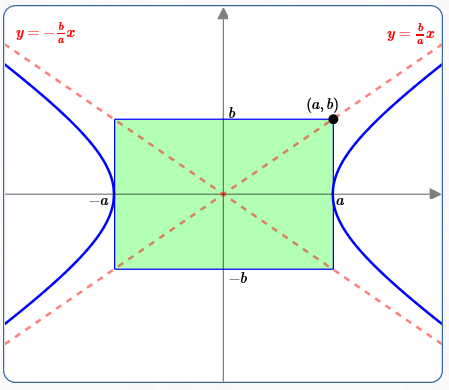
The lines $\,y = \pm\frac bax\,$ are asymptotes for the hyperbola $\,\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\,.$

As $\,x\,$ gets big (positive or negative), the graph of $\,\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\,$ gets closer and closer to these lines, as shown above.

The asymptotes form an ‘envelope’ inside which the hyperbola lives. The envelope gets tighter and tighter as $\,x\,$ gets bigger and bigger!

The green box is called the central box of the hyperbola, and is a useful graphing aid:

• Its sides are parallel to the axes
• It passes through the vertices of the hyperbola
• It crosses the other axis at $\,\pm b$

The diagonals of the central box are the asymptotes for the hyperbola!

Asymptotes for $\,\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1$

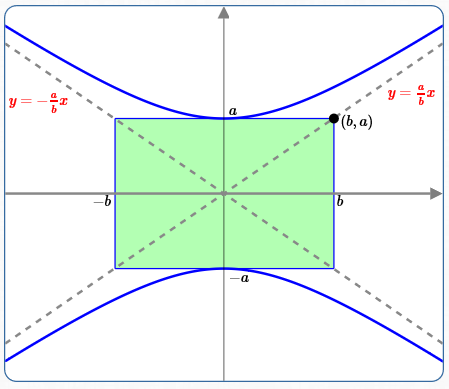
Similarly, the lines $\,y = \pm\frac abx\,$ are asymptotes for the hyperbola $\,\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1\,.$

Compare $\,\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1\,$ with the previously-discussed equation $\,\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\,$:  the variables $\,x\,$ and $\,y\,$ have just been switched.

Thus, the exact same derivation as before (with variables switched) yields the asymptotes $\,x = \pm \frac ba y\,.$ Solve for $\,y\,$ to get the asymptotes $\,y = \pm\frac ab x\,.$

Alternatively, solve for $\,y\,$ in $\,\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1\,$ to get:

For large $\,x\,,$ the graph looks like $\,y = \pm \frac ab x\,.$

Getting the Central Box Graphically

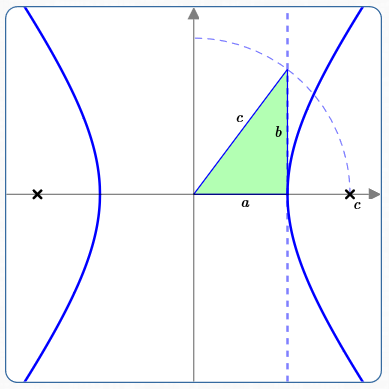
If you have a hyperbola graphed with the foci already located, then it's easy to get the central box graphically:

• Make sure that ‘$\,1\,$’ on the $x$-axis is the same as ‘$\,1\,$’ on the $y$-axis (so that a circle actually looks like a circle).
• Sweep out (part of) the circle with center at the origin and radius $\,c\,,$ as shown above.
• Mark where the circle intersects the vertical line through the vertex.
• The green triangle has hypotenuse $\,c\,$ and bottom leg $\,a\,.$
• Since $\,c^2 = a^2 + b^2\,,$ the remaining leg must have length $\,b\,.$

Of course, you can use this information in a different way: if you already have $\,a\,$ and $\,b\,$ marked, then just rotate the hypotenuse to locate the focus!

Summary: Graphing Hyperbolas

$$\cssId{s33}{\color{green}{\frac{x^2}{a^2}} - \color{red}{\frac{y^2}{b^2}} = 1}$$

Vertices:
Set $\,y = 0\,,$ solve for $\,x\,,$ to get $\,x = \pm a\,.$

The positive term ($\color{green}{\frac{x^2}{a^2}}\,$) determines the vertices!

$$\cssId{s37}{\color{green}{\frac{y^2}{a^2}} - \color{red}{\frac{x^2}{b^2}} = 1}$$

Vertices:
Set $\,x = 0\,,$ solve for $\,y\,,$ to get $\,y = \pm a\,.$

The positive term ($\color{green}{\frac{y^2}{a^2}}\,$) determines the vertices!

Use the other term to find $\,b\,$; draw in the central box.

The diagonals of the central box are the asymptotes for the hyperbola.

Steps to Graph a Hyperbola

Vertices

Find the vertices.

Central Box

Use the other term to find $\,b\,$; draw in the central box. (See the examples below.)

Diagonals

The diagonals of the central box are the asymptotes of the hyperbola.

Draw Hyperbola

Draw in the hyperbola, using the asymptotes as an ‘envelope’.

Foci

If needed, use $\,c^2 = a^2 + b^2\,$ to locate the foci.

Examples: Graphing Hyperbolas

In both examples below, there are only $\,x^2\,,$ $\,y^2\,,$ and constant terms. When the variable terms are on the same side, they have different signs. So, we know we're dealing with hyperbolas!

Example #1: Put the Equation in Standard Form

Graph: $\,9x^2 - 4y^2 = 36$
Find the vertices, central box, asymptotes, and foci.

When all the numbers ‘work out nicely’, it may be easiest to put the equation in standard form. Here, both $\,9\,$ and $\,4\,$ go into $\,36\,$ evenly (resulting in perfect square denominators).

Put the Equation in Standard Form

Get a $\,1\,$ on the right-hand side

Simplify
(This is an equation of the form $\,\frac{x^2}{a^2} - \color{red}{\frac{y^2}{b^2}} = 1\,.$ )

Find the Vertices

Set $\,y = 0\,$:  $\, \frac{x^2}{4} = 1\,,$   $\, x^2 = 4\,,$   $\, x = \pm 2$

Use the Other Term to Find $\,b\,.$ Draw the Central Box, its Diagonals, and the Hyperbola

Compare $\,\frac{y^2}{b^2}\,$ with $\,\frac{y^2}{9}\,$ to see that $\,b = 3\,.$ Mark $\,\pm 3\,$ on the $y$-axis.

Sketch in the central box and its diagonals (which are the asymptotes). Sketch the hyperbola inside the ‘envelope’ formed by the diagonals.

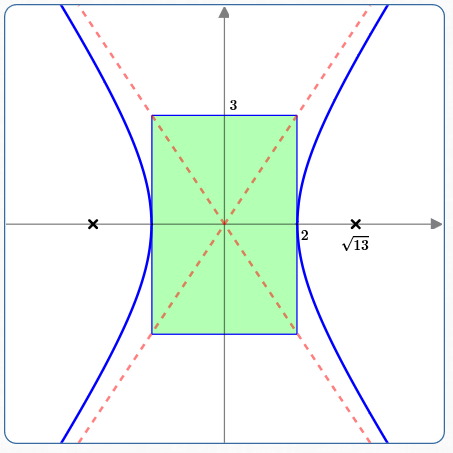
Foci

We have $\,a = 2\,$ and $\,b = 3\,$:

Report Results

Vertices:  $\,(\pm 2,0)$
Central Box:  has corners $\,(\pm 2,\pm 3)$
Asymptotes:  $\,y = \pm \frac 32x$
Foci:  $\,(\pm\sqrt{13},0)$

You'll get everything: graph, vertices, foci, asymptotes, and more!

Example #2: Don't Put the Equation (Completely) in Standard Form

If the numbers don't work out nicely, then you don't have to write it completely in standard form. As long as you get the variable terms on the left, and the ‘$\,1\,$’ on the right, you're good to go!

Graph: $\,9y^2 = 7 + 14x^2$
Find the vertices, central box, asymptotes, and foci.

Get the Variable Terms on the Left, ‘$\,1\,$’ on the Right

Variable terms on left, constant on right

Get a $\,1\,$ on the right-hand side

(This is an equation of the form $\,\frac{y^2}{a^2} - \color{red}{\frac{x^2}{b^2}} = 1\,.$ )

To go from here to ‘complete’ standard form would be a bit ugly, resulting in:

As you'll see, this isn't needed!

Find the Vertices

Set $\,x = 0\,$:  $\,\frac{9y^2}{7} = 1\,,$  $\, y^2 = \frac{7}{9}\,,$  $\, y = \pm \sqrt{\frac79} = \pm\frac{\sqrt 7}3 \approx \pm 0.88$

So:  $\,a = \frac{\sqrt 7}{3}$

Use the Other Term to Find $\,b\,.$ Draw the Central Box, its Diagonals, and the Hyperbola

Compare $\,\frac{x^2}{b^2}\,$ with $\,2x^2\,$ to find $\,b\,$:

Compare the term to the desired form

Cancel $\,x^2$

Solve for $\,b^2$

Mark $\,\pm \frac{1}{\sqrt 2}\,$ on the $x$-axis.

Sketch in the central box and its diagonals (which are the asymptotes). Sketch the hyperbola inside the ‘envelope’ formed by the diagonals.

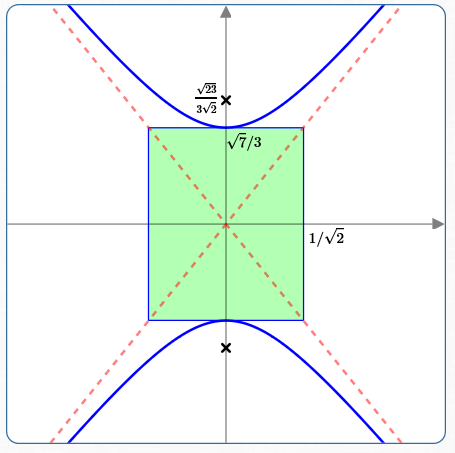
Foci

We have $\,a = \frac{\sqrt 7}{3}\,$ and $\,b = \frac{1}{\sqrt 2}\,$:

Report Results

Note that:

Vertices:  $\,\left(0 \ ,\ \pm \frac{\sqrt{7}}3\right)$

Central Box:  has corners $\,\left(\pm \frac{1}{\sqrt{2}} \ ,\ \pm \frac{\sqrt{7}}{3}\right)$

Asymptotes:  $\,y = \pm \frac{\sqrt{14}}{3}x$

Foci:  $\,\left(0 \ ,\ \pm\frac{\sqrt{23}}{3\sqrt 2}\right)$