• Jump right to the exercises!
• The concepts for this exercise are summarized below.
  For a complete discussion, read the text.
• Need some simpler practice with absolute value and related concepts first?
  Simplifying Basic Absolute Value Expressions
  Solving Simple Absolute Value Sentences
  Solving Sentences involving ‘Plus or Minus’
  Solving Absolute Value Equations
  Solving Absolute Value Inequalities Involving ‘Less Than’

This section should feel remarkably similar to the previous ones.

This section presents the tools needed
to solve absolute value inequalities involving ‘greater than’, like these: $$\begin{gather} |x|\gt 5 \\ |x + 1|\ge 3 \\ |2 - 3x| \gt 7 \end{gather} $$

Each of these inequalities has only a single set of absolute value symbols
which is by itself on the left-hand side of the sentence,
and has a variable inside the absolute value.
The verb is either   ‘$\,\gt\,$’ (greater than)   or   ‘$\,\ge\,$’ (greater than or equal to).

As in the previous sections, solving sentences like these is easy,
if you remember the critical fact that absolute value gives distance from $\,0\,$.

Keep this in mind as you read the following theorem:

Recall first that normal mathematical conventions dictate that   ‘$\,|x| \gt k\ $’   represents an entire class of sentences,
including the members   ‘$\,|x| \gt 2\ $’,   ‘$\,|x| \gt 5.7\ $’,   and   ‘$\,|x| \gt \frac{1}{3}\,$’.
The variable [beautiful math coming... please be patient] $\,k\ $ changes from sentence to sentence, but is constant within a given sentence.

Recall that   ‘$\,x\lt -k\ \ \text{ or }\ \ x\gt k\ $’   is an   ‘or’   sentence, where that's the mathematical word ‘or’.
An ‘or’ sentence is true when at least one of the subsentences is true.
Thus, the sentence ‘$\,x\lt -k\ \ \text{ or }\ \ x\gt k\ $’ is true
for all the numbers to the left of $\,-k\,$, put together with all the numbers to the right of $\,k\ $:

the values of $\,x\,$ that make the sentence ‘$\,x\lt -k\ \ \text{ or }\ \ x\gt k\ $’ true (for $\,k \gt 0$)

When you see a sentence of the form [beautiful math coming... please be patient] $\,|x| \gt k\ $, here's what you should do:

• Check that [beautiful math coming... please be patient] $\,k\,$ is a nonnegative number (greater than or equal to zero).
• The symbol [beautiful math coming... please be patient] $\,|x|\,$ represents the distance between $\,x\,$ and $\,0\,$.
• Thus, you want the numbers [beautiful math coming... please be patient] $\,x\,$, whose distance from $\,0\,$ is greater than $\,k\ $:
           
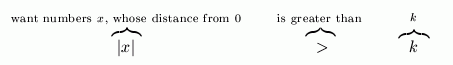
• You can walk from $\,0\,$ in two directions: to the left, or to the right.
  Walk more than $\,k\,$ units to the left, and you get all the numbers to the left of $\,-k\ $.
  Walk more than $\,k\,$ units to the right, and you get all the numbers to the right of $\,k\ $.
  Throw these two sets together!
           
• Thus,   $\,|x| \gt k\ $   is equivalent to   $\,x\lt -k\ \ \text{ or }\ \ x\gt k\ $.
• Equivalent sentences are completely interchangeable, and you can use whichever is easiest to work with.
  In this case, you're getting rid of the troublesome absolute value in exchange for a less-troublesome compound inequality.

Recall that   ‘$\,\text{⇔}\,$’   is a symbol for ‘is equivalent to’.

The power of the sentence-transforming tool   ‘$\,|x| \gt k\ \ \ \text{⇔}\ \ \ \,x\lt -k\ \ \text{ or }\ \ x\gt k\ $’
goes far beyond solving simple sentences like [beautiful math coming... please be patient] $\,|x| \gt 5\,$!

Since $\,x\,$ can be any real number, you should think of [beautiful math coming... please be patient] $\,x\,$ as merely representing
the stuff inside the absolute value symbols.
Thus, you could think of rewriting the tool as:   ‘$\,|\text{stuff}| \gt k\ \ \ \text{⇔}\ \ \ \text{stuff}\lt -k\ \ \text{ or }\ \ \text{stuff}\gt k\ $’

See how this idea is used in the following examples: