Summary: Equations of Ellipses in Standard Form

For lots more information on ellipses, see these earlier sections:

Summary:  Equations of Ellipses with Centers at the Origin and Foci on the $x$-axis or $y$-axis

Foci on the $x$-axis

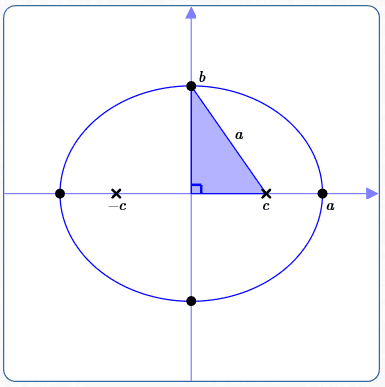
Equation of Ellipse:

$$\cssId{s12}{\frac{x^2}{\underset{\text{bigger}}{\underset{\uparrow}{a^2}}} + \frac{y^2}{b^2} = 1}$$

When the foci are on the $\color{red}{x}$-axis, the bigger number ($\,a^2 \gt b^2\,$) is beneath the $\,\color{red}{x}^2\,.$

Coordinates of foci: $\,(-c,0)\,$ and $\,(c,0)\,$

Foci on the $y$-axis

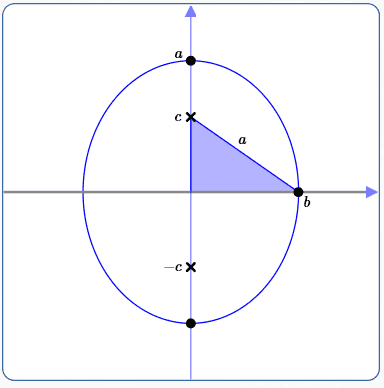
Equation of Ellipse:

$$\cssId{s19}{\frac{x^2}{b^2} + \frac{y^2}{\underset{\text{bigger}}{\underset{\uparrow}{a^2}}} = 1}$$

When the foci are on the $\color{red}{y}$-axis, the bigger number ($\,a^2 \gt b^2\,$) is beneath the $\,\color{red}{y}^2\,.$

Coordinates of foci: $\,(0,-c)\,$ and $\,(0,c)\,$

Tips

Recognizing an Ellipse in Standard Form

The key to recognizing the equation of an ellipse with center at the origin and foci on either the $x$-axis or $y$-axis is this:

• It has only $\,x^2\,,$ $\,y^2\,,$ and constant terms.
• When the $\,x^2\,$ and $\,y^2\,$ terms are on the same side of the equation, then they must have the same sign.

The Bigger Denominator Locates the Foci

When the bigger number is beneath the $\,x^2\,$ term, then the foci are on the $x$-axis.

When the bigger number is beneath the $\,y^2\,$ term, then the foci are on the $y$-axis.

Look for the bigger denominator to tell you where the foci lie!

Getting Intercepts

Cut down on memorization—just use standard techniques to get the $x$ and $y$ intercepts.

For example, in the equation $\,\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\,$:

Let $\,y = 0\,$ to get the $x$-intercepts $\,a\,$ and $\,-a\,$:

Let $\,x = 0\,$ to get the $y$-intercepts $\,b\,$ and $\,-b\,$:

Finding the Foci

To find the foci:  $\,c^2\,$ is always the bigger denominator minus the smaller denominator.

Example: Graphing an Ellipse

Graph:  $100 - 4x^2 = 25y^2$

Initial thoughts:  There are only $\,x^2\,,$ $\,y^2\,$ and constant terms. When the $\,x^2\,$ and $\,y^2\,$ terms are on the same side of the equation, they have the same sign. It's an ellipse with center at the origin and foci on either the $x$-axis or $y$-axis!

Solution

$x$-intercepts (set $\,y = 0\,$):  $\,x = \pm 5\,$

$y$-intercepts (set $\,x = 0\,$):  $\,y = \pm 2\,$

Foci:  The bigger number is under the $\,x^2\,,$ so the foci are on the $x$-axis.

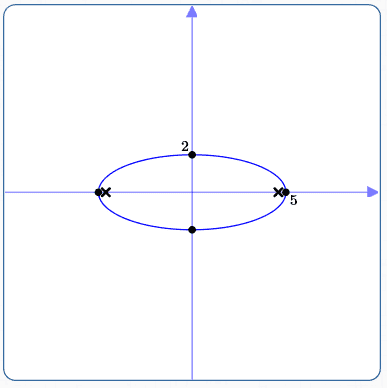
Example: Finding the Equation of an Ellipse

Find the equation of the following ellipse:

• Center at the origin
• Major axis along the $y$-axis, with length $\,8$
• Minor axis has length $\,6$

Also, find the coordinates of the foci.

Solution

Since the major axis is along the $y$-axis, the form of the equation is:

$a\,$ is half the length of the major axis, which is: $\,\frac{8}{2} = 4$

$b\,$ is half the length of the minor axis, which is: $\,\frac{6}{2} = 3$

The equation is:

Foci:  $\,c^2 = a^2 - b^2 = 16 - 9 = 7\,,$ so $\,c = \pm\sqrt{7}\,.$

Coordinates of foci:  $\,(0,-\sqrt{7})\,$ and $\,(0,\sqrt{7})$